🐸 DFS(Depth-First Search) : 깊이 우선 탐색
-
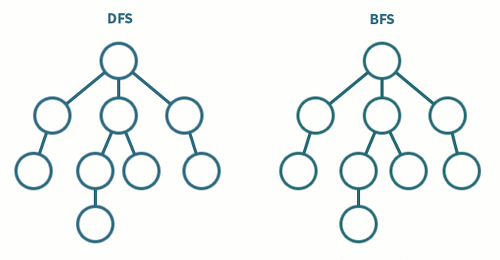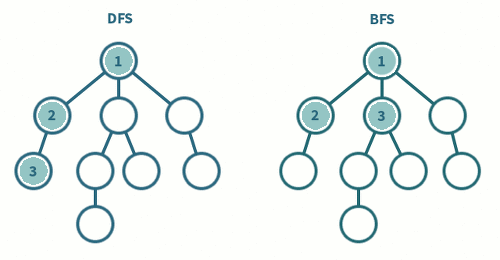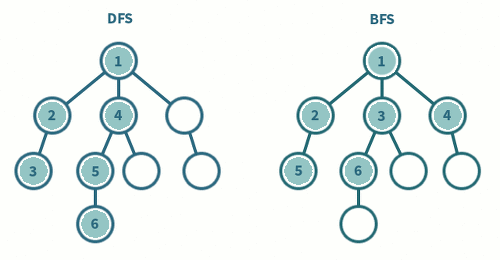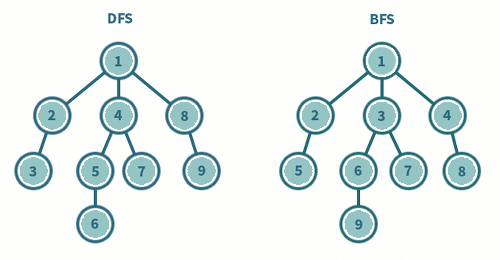
DFS는 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
-
스택 자료구조 ( 혹은 재귀함수) 를 이용하며, 구체적인 동작 과정은 다음과 같다.
1) 탐색 시작 노드를 스택에 삽입하고 방문 처리한다.
2) 최택의 최상단 노드에 방문하지 않은 인접한 노드가 하라나도 있으면 그 노드를
스택에 넣고 방문 처리한다. 방문 하지 않은 인접 노드가 없으면 스택에서 최상단
노드를 꺼낸다.
3) 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.- 내가 작성한 코드는 아래와 같다.
import java.util.ArrayList; import java.util.Stack; public class DepthFirstSearch { public void search(ArrayList<ArrayList<Integer>> arrayList, Integer start) { Stack<Integer> stack = new Stack<>(); Integer index = 0; stack.push(start); // 시작점을 넣으면 시작점의 리스트로 이동 ArrayList<Integer> visitNum = new ArrayList<>(); System.out.print("탐색 순서 : " + start + " "); while (!stack.empty()) { int i = 0; while(i < arrayList.get(start).size() && index > -1) { Integer min = arrayList.get(start).get(i); if(i == arrayList.get(start).size()-1) { if(!stack.contains(min) && !visitNum.contains(min)) { stack.push(min); index++; System.out.print(min + " "); start = min; break; } else { visitNum.add(stack.pop()); index = index - 1; if(index > -1) { start = stack.get(index); } else { break; } } } if(!stack.contains(min) && !visitNum.contains(min)) { stack.push(min); start = min; index++; System.out.print(min + " "); break; } else { i = i+1; } } } } }
🦁 BFS(Breadth-First Search) : 너비 우선 탐색
-
BFS는 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘이다.
-
큐 자료구조를 이용하며, 구체적인 동작 과정은 다음과 같다.
1) 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
2) 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에는 방문하지 않은 노드를 모두
큐에 삽입하고 방문 처리한다.
3) 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.- 내가 작성한 코드는 아래와 같다.
import java.util.*; public class BreadthFirstSearch { public void search(ArrayList<ArrayList<Integer>> arrayList, Integer start) { Queue<Integer> queue = new LinkedList<>(); queue.add(start); // 시작점을 넣으면 시작점의 리스트로 이동 ArrayList<Integer> visitNum = new ArrayList<>(); visitNum.add(start); System.out.print("탐색 순서 : " + start + " "); while (!queue.isEmpty()) { int i = 0; while (i < arrayList.get(start).size()) { Integer num = arrayList.get(start).get(i); if (i == arrayList.get(start).size() - 1) { if (!queue.contains(num) && !visitNum.contains(num)) { queue.add(num); visitNum.add(num); System.out.print(num + " "); queue.remove(); start = queue.peek(); break; } else { queue.remove(); start = queue.peek(); break; } } if (!queue.contains(num) && !visitNum.contains(num)) { queue.add(num); visitNum.add(num); System.out.print(num + " "); break; } else { i = i+1; } } } } } - 내가 작성한 코드는 아래와 같다.
-
구현하는데는 성공했지만 딱봐도 코드가 너무 깔끔해보이지 못하는 것을 내가봐도 느꼈다. 그래서 아래는 수업시간에 배운 코드로 다시 올려본다.
-
딱 봐도 훨씬 간결해보이는 것을 볼 수 있다. 앞으론 구현되는것도 좋치만, 어떻게 코드를 간결하고 보다 더 들여쓰기를 안하고 작성할 수 있을까에 대한 고민을 많이 해봐야겠다는 생각이 든다.
import java.util.Collections;
import java.util.List;
import java.util.Stack;
// ✅ 깊이 우선 탐색 (스택 사용)
public class Dfs {
public void search(List<List<Integer>> lists, Integer startNum) {
boolean[] visited = new boolean[lists.size()];
Stack<Integer> stack = new Stack<>();
stack.push(startNum);
System.out.print("깊이 우선 탐색 : ");
while (!stack.isEmpty()) {
int node = stack.pop();
if (!visited[node]) {
System.out.print(node + " ");
visited[node] = true;
List<Integer> neighbors = lists.get(node);
Collections.reverse(neighbors);
for (int neighbor : neighbors) {
if (!visited[neighbor]) {
stack.push(neighbor);
}
}
}
}
System.out.println();
}
// ✅ 깊이 우선 탐색 (재귀 활용)
public void searchRecursive(List<List<Integer>> lists, Integer startNum) {
System.out.print("깊이 우선 탐색 : ");
searchRecursive(lists, startNum, new boolean[lists.size()]);
System.out.println("재귀 방식");
}
public void searchRecursive(List<List<Integer>> lists, int node, boolean[] visited) {
if (!visited[node]) {
System.out.print(node + " ");
visited[node] = true;
List<Integer> neighbors = lists.get(node);
Collections.reverse(neighbors);
for (int neighbor : neighbors) {
searchRecursive(lists, neighbor, visited);
}
}
}
}
import java.util.*;
// ✅ 너비 우선 탐색 (큐 사용)
public class Bfs {
public void search(List<List<Integer>> lists, Integer startNum) {
boolean[] visited = new boolean[lists.size()];
Queue<Integer> queue = new LinkedList<>();
queue.add(startNum);
visited[startNum] = true;
System.out.print("너비 우선 탐색 : ");
while (!queue.isEmpty()) {
int node = queue.poll();
System.out.print(node + " ");
List<Integer> neighbors = lists.get(node);
for (int neighbor : neighbors) {
if (!visited[neighbor]) {
queue.add(neighbor);
visited[neighbor] = true;
}
}
}
System.out.println();
}
}
🐼 Greedy(탐욕법) 알고리즘
-
그리디 알고리즘은 최적의 값을 구해야 하는 상황에서 사용되는 근시안적인 방법론으로 "각 단계에서 최적이라고 생각되는 것을 선택" 해 나가는 방식으로 진행하여 최종적인 해답에 도달하는 알고리즘이다.
-
이때, 항상 최적의 값을 보장하는것이 아니라 최적의 값에 "근사한 값" 을 목표로 한다.
-
주로 문제를 분할 가능한 문제들로 분할한 뒤, 각 문제들에 대한 최적해를 구한 뒤 이를 결합하여 전체 문제의 최적해를 구하는 경우에 주로 사용된다.
-
그리디 알고리즘의 주요 속성
1) 탐욕 선택 속성(Greedy Choice Property)
➡ 각 단계에서 최적의 선택을 했을 때 전체 문제에 대한 최적해를 구할 수 있는
경우를 말한다. 즉, 각 단계에서 가장 이상적인 선택을 하는 것이 전체적으로 최적의
결과를 가져온다는 것이다.2) 최적 부분 구조(Optimal Substructure)
➡ 전체 문제의 최적해가 부분 문제의 최적해로 구성될 수 있는 경우를 말한다.
즉, 전체 문제를 작은 부분 문제로 나누어 각각의 부분 문제에서 최적의 해를
구한 후 이를 조합하여 전체 문제의 최적해를 구하는 것을 의미한다. -
DFS/BFS 와 그리디 알고리즘에 대한 추가 문제풀이는 프로그래머스 이용 풀이하여 프로그래머스 시리즈에 따로 정리해 두겠다.
오늘의 느낀점 👀
-
오늘은 알고리즘 3일차로 깊이 우선 탐색 / 너비 우선 탐색, 그리고 그리디 알고리즘을 학습하고 실전 문제들을 프로그래머스를 이용하여 풀어봤다.
-
결과적으로 말하면 참패였다... 정확하게 채점결과 정답이 나온것이 1문제 밖에 없었는데 생각보다 너무 어려워서 멘붕이었다. 가장 핵심은 문제를 읽고 이것을 어떤 알고리즘을 사용하면 쉽게 풀이할 수 있겠다 라는 생각이 드는것이라 생각한다.
-
결국 답은 문제를 많이 풀어보고 익히는 방법밖엔 없다는걸 잘 안다. 다시 한번 경각심을 갖고 프로그래머스 문제는 취뽀하는 그날까지 꾸준히 풀어보겠다.
