목차
1. Intro
2. Eigenvector Centrality
3. Betweenness Centrality
4. Closeness Centrality

1. 개요

Traditional Methods for Machine Learning in Graphs

Graph에 대한 전통적인 머신러닝의 방법론은 node, edge 그리고 Graph 자체에 대한 feature를 구하는 것으로 부터 시작한다. feature를 손수 구한 다음 Random Forest, SVM, Neural Network에서 돌려서 예측을 수행하는 것이다.

Feature Design은 모델의 성능을 좌우하는 핵심적인 요소이기 매우 중요하며, Graph의 요소 및 전체 그래프에 대한 feature를 손수 구해야 했으며, feature를 구하는데 한가지 중요한 요소는 node의 중요도였다. 어떤 노드가 얼마나 중요한 노드인지 알기 위해 Centrality라는 개념을 알 필요가 있었다. Centrality를 구하기 위해 3가지 대표적인 방법이 있다.

하나는 Eigenvector Centrality,
둘째는 Betweenness Centrality,
셋째는 Closeness Centrality이다.

2. Eigenvector Centrality

Eigenvector Centrality는 Spectral Clustering에서 Eigenvalue를 이용해 클러스터링을 한 것을 참고 하면 조금더 이해가 쉽다. Spectral clustering에서 clustering을 하는 방법은 순서대로 나열 된 Eigenvalue들 중에서 차이가 커지는 Eigenvalue에서 끊는 것이었다. Eigenvalue가 커지면 커질 수록 연결된 노드가 많아진 다는 의미였기 때문에 더 작은 Eigenvalue에 끊었다. 이와 마찬가지로 Eigenvalue Centrality에서 높은 eigenvalue일 수록 더 많이 연결되어 있다고 볼 수 있음으로, 더 중요한 노드로 간주하는 것이다. 간단하게 말해 노드 v 가 연결 다른 노드와 연결 되어 있을 때, 연결된 이웃노드들이 중요할 경우, 노드 v도 중요도가 높아지는 방식이다. 그리고 이 중요도는 eigenvector로 나타난다.

Eigenvector Centrality를 구하는 공식은 아래와 같다.

$\lambda c = Ac \rightarrow c_v = \frac 1 \lambda \underset{u \in N(v)} {\sum}$

그런데 여러개의 eigenvalue가 나올 텐데, 항상 유일한 가장 큰 eigenvalue가 나온다고 어떻게 확신하는가? 이는 Perron-Frobenius Theorem에 따라 양수의 실수 행렬의 경우 유일한 가장 큰 eigenvalue가 존재함을 보장한다.

PageRank 알고리즘도 Eigenvector Centrality의 아류중 하나이다. PageRank 역시 연결된 노드의 중요성에 따라 해당 노드의 중요성이 결정되는 구조이다.

3. Betweenness Centrality

Betweenness Centrality는 노드 v 가 있다고 했을 때, 노드 a 에서 노드 b로 가는 shortest path 들 중에서 노드 v를 거치는 개수로 노드 a 에서 노드 b로 가는 shortest path 개수를 나눈 값이다.

공식으로 나타내면 아래와 같다.

$c_v = \underset{s\ne v\ne t}{\sum}\frac {\#(\text{shortest paths between s and t that contain v})} {\# \text{(shortest paths between s and t)}}$

예시 코드를 적오보면 아래와 같다.

import networkx as nx

g = nx.Graph()

g.add_edges_from([
    ["a", "c"],
    ["c", "b"],
    ["c", "d"],
    ["d", "e"],
    ["b", "d"]
    ]
)

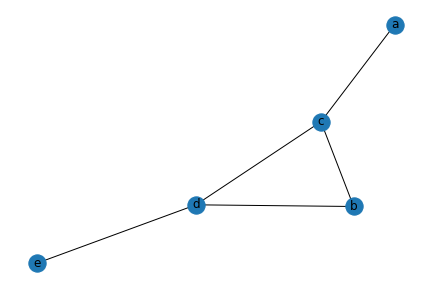
nx.betweenness_centrality(g)

{'a': 0.0, 'c': 0.5, 'b': 0.0, 'd': 0.5, 'e': 0.0}

betweenness_centrality를 구하면 위와 같은데 c, d에서 0.5가 나온 이유는 아래와 같다.
먼저 c 노드가 0.5의 centrality를 가지고 있는 이유는

(a-c-b, a-c-d, a-c-d-e) 3개
(a-c-b, a-c-d, a-c-d-e, b-d-e, c-b-d, c-d-e) 6개

그러므로 3/6 = 0.5 이다. 즉 노드 v -> u로 가는 가장 빠른 path에서 우리가 betweenness를 구하려는 노드가 중간에 있을 확률이 얼마냐이다.

마찬가지로 d 역시 계산해 보면 동일한 결과를 얻을 수 있다.

3. Closeness Centrality

Closeness Centrality는 노드 a 에서 노드 b로 가는 가장 짧은 path의 길이들의 합을 이용해 중요도를 계산하는 방식이다. 공식은 아래와 같다.

$c_v = \frac {n-1} {\underset{u\ne v} {\sum}\text{shortest path length between u and v}}$

n-1은 전체 노드 개수 n에서 자기 자신인 노드 v를 제외한 개수이다.

예를 들어 Betweeness Centrality에서 예시로 사용했던 그래프의 Closeness Centrality를 구하면

nx.closeness_centrality(g)

{'a': 0.5, 'c': 0.8, 'b': 0.6666666666666666, 'd': 0.8, 'e': 0.5} 이 출력된다.

노드 a 의 경우 (a-c-b, a-c, a-c-d, a-c-d-e) -> 4 / (2 + 1 + 2 + 3) = 4/8 = 0.5

노드 d의 경우 (d-c-a, d-b, d-c, d-e) -> 4 / (2 + 1 + 1 + 1) = 4 / 5 = 0.8

이 된다.