이 글은 William Fleshman의 Spectral Clustering을 참고 하여 일부 번역 및 수정을 하여 올림을 알려드립니다.

Intro

클러스터링은 Machine Learning의 주요 이슈중에 하나입니다. 특히, 데이터가 주어져 있지만 라벨이 존재하지 않을 경우, 클러스터링 알고리즘으로 라벨을 자동으로 붙여주는 것만으로도 충분히 학습이 가능하기 때문입니다. 그래서 우리의 목적은 라벨되지 않은 데이터를 그룹 짓고, 가능한한 비슷한 데이터가 같은 그룹에 속하게 하는 것입니다.

Spectral Clustering은 그래프 이론에 그 뿌리를 두고 있습니다. 노드와 엣지로 연결된 그래프에서 노드들의 Communities를 찾아내는 것을 목적으로 합니다.

Spectral Clustering은 그래프 데이터로부터 뽑아낸 Eigenvalues와 Eigenvectors로부터 Clustering에 중요한 정보들을 뽑아내어 클러스터링을 시도합니다. Eigenvalues로부터 Spectrum을 확인하고, Eigenvector에서 군집을 할 데이터를 얻어 냅니다.

(Graph, Adjacency matrix는 알고 계시다고 깔고 가겠습니다.)

Related

Eigenvectors and Eigenvalues

Spectral Clustering에서 가장 중요한 개념은 Eigenvector와 Eigenvalues입니다. 어떤 행렬 연산 $Ax = y$ 가 있다고 했을 때, $Ax = \lambda x$, 즉 행렬방정식의 값이 연산에 사용한 vector의 scalar multiplication $\lambda$라고 했을 때, 이 때 사용된 $x$를 eigenvector, 그리고 $\lambda$ 를 eigenvalue 라고 합니다.

Graph Laplacian

Graph Laplacian이란 Graph를 표현하기 위한 하나의 Matrix의 표현입니다. Graph Laplacian을 계산하는 것은 간단합니다. 각 노드의 Degree를 주대각성분으로 하는 대각행렬에서 인접행렬을 빼는 것입니다. numpy를 이용하여 간단하게 구현할 수 있습니다.

import numpy

D = np.diag(np.sum(adjacency_matrix, axis=1))

# Graph Laplacian
L = D - adjacency_matrix

Spectral Clustering(Sample)

Eigenvalues of Graph Laplacian

그렇다면 Spectral Clustering에서 어떻게 Eigenvalue와 Eigenvector가 사용될까요? 아래의 그림을 보면서 그래프의 특징에 따라, Eigenvalue의 값이 변화되는 것을 따라가면 이해 할 수 있습니다.

왼쪽의 그래프가 Eigenvalue들의 크기를 작은순부터 큰 순으로 나열한 것이고, 오른쪽 그래프는 Graph에서 edge를 하나씩 추가해 나간 것입니다. 오른쪽 Graph에서 Edge를 추가해 나갈 수록 Eigenvalue들이 점차 오른쪽부터 올라가는 것을 보실 수 있습니다. 왼쪽 그래프에서 살펴보아야 할 점은 eigenvalue들 중 0인 eigenvalue들의 개수입니다. 맨처음 Graph에서 edge가 한개만 존재 했을 경우에는 0의 개수가 8개인 것을 볼 수 있습니다. 그리고 edge가 한개 더 추가 되었을 때, 0의 개수가 7개로 변합니다. 하지만 세번째 연결에서는 그대로 0인 eigenvalue의 개수가 7개인체로 그대로 있습니다. 이를 통해 우리는 eigenvalue의 0인 값의 개수가 Graph에서 서로 edge로 연결되지 않은 노드들의 집합의 개수라는 것을 알 수 있습니다. 따라서 Graph에서 edge가 추가됨에 따라, 연결되지 않은 노드들의 집합의 개수가 줄어들게 되어 0인 eigenvalue들의 개수가 점차 줄어들게됩니다. 맨 마지막 edge가 추가되어 모든 node간에 path가 존재할 때, 0의 개수가 1개만 남게 되는 것은 그런 이유입니다.

Clustering

그렇다면 eigenvalue정보를 가지고 어떻게 하면 Clustering을 할 수 있을까요? 그 정보는 eigenvalue의 0개수가 아니라 eigenvalue 값에 의해 추론 될 수 있습니다. 위의 그래프에서 맨 마지막 스탭에 완성되는 Graph에서 2번째 eigenvalue가 상당히 작다는 것을 볼 수 있습니다.

이 두번째 eigenvalue를 Fiedler value라고 부르며, 두번째 eigenvalue에 대응되는 eigenvector를 Fiedler vector라고 합니다. 이 Fiedler value는 Graph를 두개의 Community로 만들기 위해 잘라내야할 최소한의 횟수를 추정합니다. 즉, Fiedler value가 작다는 것은 적은 수의 edge를 잘라내어 Graph를 2개로 만들 수 있다는 것입니다. Graph에서 Community는 서로간에 밀집하게 연결되어 있고, 서로다른 Community는 적은 edge로 연결되어 있다고 볼 수 있음으로, 더 적은 수의 edge를 잘라내어 Graph를 여러개로 만든다는 것은 Community를 찾는것으로 귀결됩니다. 보통 갑자기 eigenvalue가 커지는 지점을 clustering 지점으로 볼 수 있습니다.

그렇다면 어떻게 하면 Graph를 Clustering 할 수 있을 까요? 아직 나오지 않은 eigenvector가 그 역할을 할 것입니다. 방법은 Eigenvalue의 순서대로 Eigenvector를 나열합니다. 그리고 eigenvector들을 원하는 Clustering 개수로 쳐냅니다. 마지막을 KMeans나 다른 군집 알고리즘을 사용해 eigenvectors를 군집화 하면 완성입니다.

import numpy as np
from sklearn.cluster import KMeans

n_cluster = 2

# Graph Laplacian
L = D - adjacency_matrix

# Eigenvalue, Eigenvectors
vals, vecs = np.linalg.eig(L)

# Sort Eigenvector 
vecs = vecs[:,np.argsort(vals)]

# Cluster by KMeans
kmeans = KMeans(n_clusters=n_cluster)

kmeans.fit(vecs[:, 1:n_cluster])

labels = kmeans.labels_

위의 클러스터링 된 라벨 정보를 바탕으로 다시 그래프를 그려보면 아래와 같습니다. 먼저 n_cluster = 2 일 경우

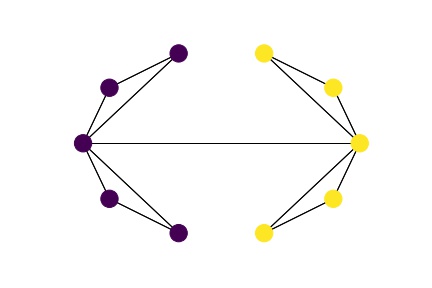
n_cluster = 4 일 경우

올바르게 클러스터링 된 것을 볼 수 있습니다.

Spectral Clustering(Football Club)

Football Club Graph를 가져와 Spectral Clustering을 돌려보았습니다. 원래 그래프는 아래와 같습니다.

하지만 Spectral Clustering을 수행하면 먼저 eigenvalue 스펙트럼을 얻을 수 있습니다.

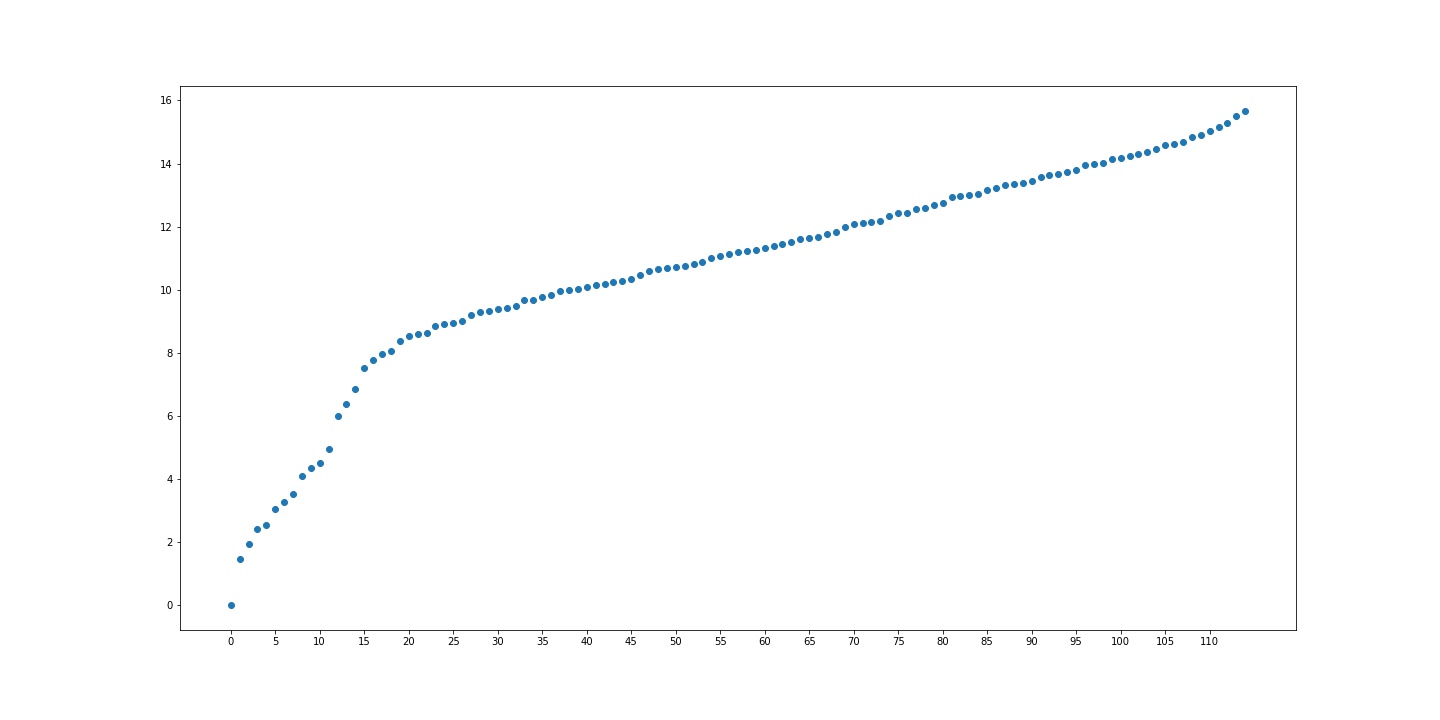
n_cluster가 5일 경우

n_cluster가 12일 경우

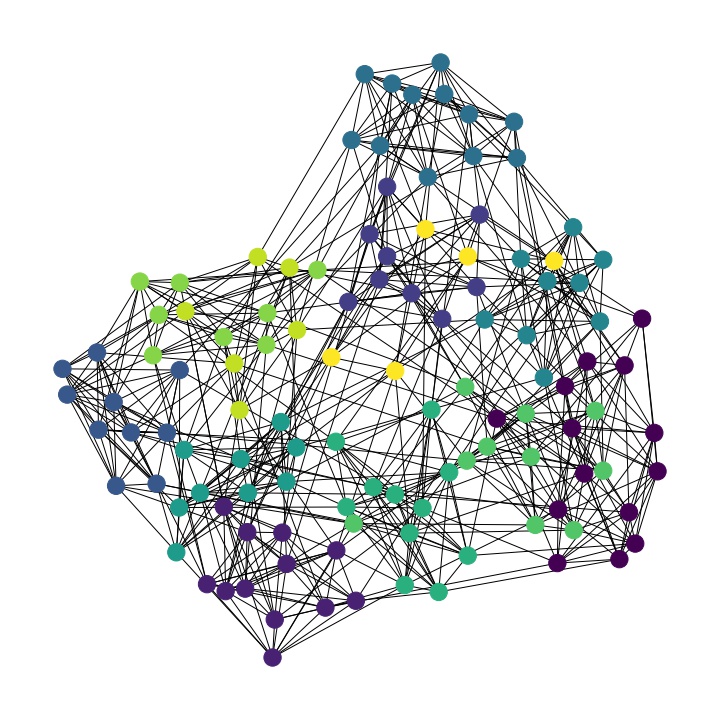
그럴 듯 하게 clustering이 된 것을 볼 수 있습니다.

Conclusion

지금까지 Spectral Clustering에 대해 간단하게 알아 보았습니다. 이 알고리즘은 Graph를 clustering 하여 community를 찾아내기에 간단하고 적합한 방법이지만 몇가지 단점이 있는 것으로 보였습니다. 첫번째는 몇개의 군집으로 나눌지를 결정해 줘야 하는 것이었고, 두번째는 인접행렬을 사용하여 Graph Laplacian을 만들어야 함으로, Graph의 사이즈가 매우 클 때, 연산에 적합하지 않을 것으로 보였습니다.(node 개수가 많아질 수록 $n^2$으로 인접행렬 크기가 늘어난다.) 그럴지라도, 앞으로 더 나은 Graph Clustering 방법론들을 배울 좋은 기본 방법론을 배울 수 있었습니다.