1. Transcription Networks

※이 요약노트는 독자가 분자생물학에 대한 기초적인 내용을 인지하고 있다는 가정하에 썼음 밝힌다. 또한 이 내용은 Uri Alon의 An introduction to system biology - Design Principles of Biological Circuits의 내용임을 알리는 바이다.

    Central Theroem에 따르면 DNA로부터 mRNA가 생성되고, mRNA가 ribosome에서 Amino Acid의 Polypeptide(단백질)를 생성한다. 그러나 단순하게 mRNA가 단백질이 되는 것이 아니라 그 과정에서 다수의 Activator, Regressor 단백질이 Gene의 promotger에 관여함으로써, 세포내에서의 혹은 체내에서의 특정 단백질의 농도가 결정된다. 특히 DNA로부터 mRNA로 전사되는 과정을 Transcription 이라 부르며, 다수의 단백질이 Transcription 과정에 관련되는 것을 Node와 Edge로 표현되는 Graph로써 표현 될 수 있다. Transcription Networks 에서는 기본 Building Block인 Transcription network의 node간 edge에 대해 알아본다. (여기서 node는 단백질을 의미하고, source 노드는 activator/regressor 를 의미하고, target node는 source노드에 의해 조절(regulated)되는 단백질을 의미한다.)

1.3 Elements of Transcription Networks

    어떤 세포가 있을 때, 그 세포는 환경에 따라 다르게 작동하며, 그 근본은 세포막에서 외부 환경의 변화(stress)를 포착하면, 내부 activator / regressor가 특정 gene의 promoter에 작용하거나 덜 작용함으로써, RNAp(RNA Polymaese)의 활동성을 증진시키거나 억제하게 된다.
   이 작용은 과정에 따라 다른 시간 scale을 가진다. 어떤 전사 요소(transcription factor)를 활성화(activation)시키는 데는 수초내로 가능하지만, 실제 전사가 일어나는 것은 수분이 소요 된다. 그리고 전사가 일어나서 단백질로 번역(translate)되는데 까지는 몇 시간이 걸린다. 그러므로 시간이 천천히 흐른다면 단백질의 농도는 일정하게 유지되는 steady state에 이르게 된다.
    다른 주목할만한 전사 네트워크의 특징은 Modularity 이다. 즉, 한 생명체의 유전자를 다른 생명체에 붙여서 전사시켜, 이전에는 만들 수 없었던 단백질을 생성해 낼 수 있는 것이다. 예를 들면 GFP(Green fluorescent protein)이라는 초록색을 나타내게 하는 gene을 jellyfish(해파리)로부터 다른 bacteria의 DNA로 이식하면, 그 박테리아는 초록색을 나타낸다. 또는 GFP를 E.coli의 sugar inducible gene의 promoter 앞에 박아 놓으면, E.coli가 그 gene을 발현 할 때마다 초록색으로 변한다. 이런 Modularity는 진화에서 특이적으로 나타난다. 예를 들면 쥐와 인간은 매우 비슷한 유전자를 가지고 있지만 완전히 다른 특징을 가진다. 이는 DNA가 같더라도, 다른 전사 네트워크로 인해, 즉 서로 다른 조절로 인해 그 결과는 완전히 달라질 수 있다.

1.3.3 The Numbers of on Arrows: Input Functions

    위에서 간단하게 언급했듯이, 어떤 시그널이 들어와, activator/regressor를 활성화 시키면, 단백질의 생성 속도가 높아진다. activator / regressor의 활성에 따라 gene의 promoter가 활성화/억제 되는 것을 아래와 같이 표기할 수 있다.

Activator의 경우

$X \mapsto Y$로 표현,

Regressor의 경우

$X \dashv Y$ 로 표기한다.

하지만 단순히 이렇게만 표기하는 것은 농도의 개념을 적용 할 수 없음으로, Hill function $Y = f(X^*)$를 아래와 같이 정의 할 수있다.($X^*$ 은 activator, regressor의 농도를 의미한다.)

Hill function for Activator

$f(X^*) = \beta\frac{X^{*n}}{K^{n} + X^{*n}}$

Hill function for Regressor

$f(X^*) = \beta\frac{K^{n}}{K^{n} + X^{*n}}$

예를 들어 $K = 5, \beta = 10$ 일때, activator와 regressor 그래프는 figure 1과 figure 2와 같다.

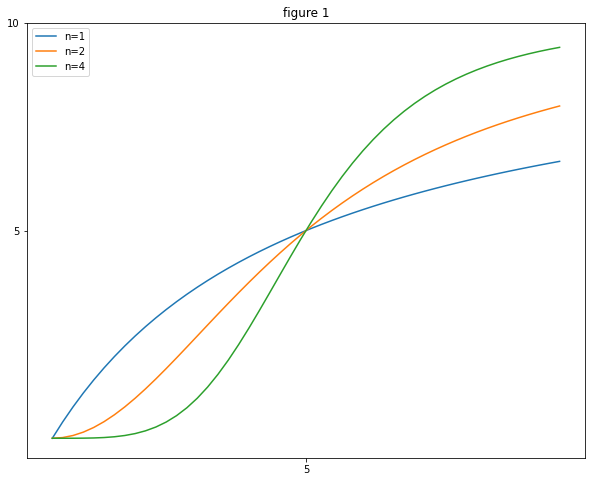
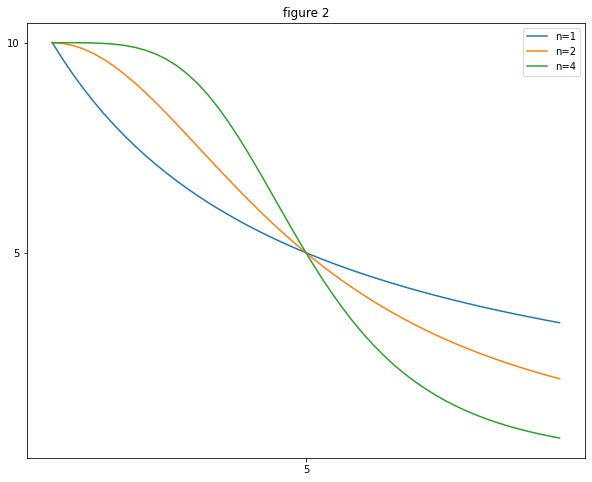
• $K$ : Activation coefficient
  It defines the concentration of active $X$ needed to significantly activate expression
• $\beta$ : Maximal promoter activity
  $\beta$ is reached at high activator concentrations, $X^* \gg K$
  
• $n$ : Hill coefficent
  It determines the steepness of the input function. ※ 대체로 $1 \leqq n \leqq 4$ 의 Hill coefficent를 갖는다.
  

1.3.4 Logic Input Functions: A simple Framework for understanding Network dynamics

    정확한 hill function 대신에 근사로 Logic approximation 을 사용할 수 있다. hill function에서 중요한 것은 작은 값에서 큰값으로의 $X^* = K$를 기준으로 전환이다. 이 근사를 이용하여 gene의 활성을 껐다 켰다 ( $f(X^*) = 0$ or $f(X^*) = \beta$) 할 수 있다. logic approximation을 수식으로 표현하면 아래와 같이 indicator function 인 $\theta$를 사용해 표현할 수 있다. $\theta$는 어떤 evaluation이 true 일 경우 1을 그렇지 않을 경우 0을 반환하는 함수이다.

Logic approximation for activator

$f(X^*) = \beta\theta(X^* > K)$

Logic approximation for regressor

$f(X^*) = \beta\theta(X^* < K)$

1.4 Dynamics and Response time of simple regulation

    단백질의 농도는 signal이 시작되고, promoter의 활성화가 시작되고 나서, 곧바로 증감하는 것이 아니라, 시간이 지남에 따라 변화한다. 그러므로 시간에 따른 단백질의 농도 차이를 고려해야 할 필요가 있다.

     단백질은 그냥 생성되기만 하는 것이 아니다. mRNA가 생기더라도 파괴 될 수 있고, 단백질로 번역되더라도 다른 단백질에 의해 파괴 될 수 있다. 또한 농도(concentration)는 분모가 커지면 줄어 들기때문에, 세포의 크기가 커짐에 따라 동일한 몰의 분자가 있어도 농도가 줄들 수 있다. 얼마전에 올린 Molarity는 $M = \frac {\# of moles in solute}{Volue of Solution(L)}$ 와 같이 용액의 부피가 커져도 용질의 몰 수는 동일하기 때문에 농도가 줄어들게 된다. 그러므로 단백질의 파괴에 의한 요소 $\alpha_{deg}$(degradation), $\alpha_{dil}$ (dillution)을 고려한 total removal rate(per unit time) $\alpha$를 고려해야 한다.

$\alpha = \alpha_{deg} + \alpha_{dil}$

    이제 단백질의 농도를 생성과 제거의 차이로 생각을 해본다면 아래와 같은 수식으로 생각을 해 볼 수 있다.

$\frac{dY}{dt} = \beta - \alpha Y$

즉, 현재의 promoter Y의 활성화 정도를 단백질 Y의 농도에서 $\alpha$ 값을 곱한 값을 뺀 값이다. 이때, 두 상태가 평형이 되는 상태를 steady state라 하는데, $\frac{dY}{dt} = 0$이 되는 상태를 의미한다. steady state는 수식을 정리해 보면 아래와 같다.

$Y_{st} = \frac{\beta}{\alpha}$

$\alpha$가 커지면 steady state가 줄어들고, 반대로 $\beta$가 커지면 steady state가 커지는 것을 의미한다.

    만일 시그널이 갑자기 사라져서, activator가 비활성화 된다면($X^* \rightarrow X$), 단백질 농도는 시간이 지남에 따라 $\alpha$ 값에 반비례하여 줄어들게 될 것이다. 이를 수식으로 표현하면 아래와 같다.

먼저, activator 가 비활성 되기 시작된 시점 $t=0$ 으로 삼으면, 이때는 steady state이다. 즉, $Y(0) = \frac{\beta}{\alpha}$그리고 Y가 시간에 따라 감소하는 어떤 함수 $e^{-at}$와 비슷하다면 taylor series에 따라 (멕클로린 급수 이용)

$Y(t) = Y(0) + Y'(0) + Y''(0) + ... + Y^n(0)...$

$Y(t) = \frac{\beta}{\alpha}(1 + (-at) + (-at)^2 + ...$

$Y(t) = \frac{\beta}{\alpha}e^{-at}$

$Y(t) = Y_{st}e^{-at}$를 유추해 볼 수 있다.

    반대로 Y의 농도가 0이었는데, 시그널이 들어와 $X^*$이 늘어난다면 $Y(t) = Y_{st}(1-e^{-at})$로 볼 수 있다. $t=0$ 일때, 0으로 시작하여, $\lim_{t\to \infty}Y(t) = Y_{st}$ 임으로 시간이 지남에 따라 다시 steady state에 이르게 된다.

How Fast does Y decay?

이 질문의 답을 내 줄 수 있는 개념은 Response Time이다. response time 이란 $Y$가 $\beta$의 절반이 되는 시간을 $T_{1/2}$로 표기할 수 있다. 공식 $Y(t) = Y_{st}e^{-at}$에 비추어 계산해 보면

$Y(T_{1/2}) = Y_{st}e^{-aT_{1/2}} = T_{st}/2$ (양변에 $\ln$ 를 취한다.)

$T_{1/2} = \frac{\ln2}{\alpha}$

이 공식에 따르면 response time이 의존하는 것은 오로지 $\alpha$값임을 알 수 있으며, $\beta$ 값은 전혀 영향을 끼치지 못하고 있다.

1.4.1 The Response Time of Stable Proteins Is One Cell Generation

    어떤 단백질들은 $\alpha = \alpha_{deg} + \alpha_{dil}$ 에서 $\alpha_{deg} = 0$인 경우가 있다. 이런 단백질들을 stable proteins 이라 한다. $\alpha = \alpha_{dil}$ 임으로 단백질의 response time에 영향을 미치는 요인은 오로지 dillution rate 임을, 즉 세포의 성장 속도임을 알 수 있다. 또한 세포가 크기가 2개가 되어 둘로 나뉠 때에서 stable protein의 농도가 반으로 줄어듬으로,

$T_{1/2} = \frac{\ln 2}{\alpha} = \tau$ 즉, stable protein의 response time은 한 세포의 생성과 동일하다는 결론에 이른다.

Thus, response time can be limiting factor that poses a costraint for designing efficient gene circuits
이 문장은 잘 이해가 안가지만, 차후 밝혀질 것으로 예상한다.