Autoregulation

이 차트의 목적은 Negative Autoregulation이 무엇인지, 그리고 어떻게 Autoregulation이 response time을 빠르게 하는지 이해하는 것을 목적으로 한다.

2.3 Auto regulation is a network motif

Network Motif - 랜덤 네트워크에서 발생하는 것 보다 더 자주 발생하는 실제 네트워크에서의 패턴

Autogegulation - 유전자 조절이 그 유전자로 생성된 단백질에 의해 이루어지는 조절현상.

Negative autoregulation - $X \dashv X$

랜덤네트워크에서 self-link가 나타날 확률은

$N$ : # of nodes
$A$ : # of edges

$P_{self} = \frac{1}{N}$ (전체 노드중 자기 자기에게 link가 있을 확률)

이항분포에 따르면 이항분포의 기대값은 $E(x) = np$ 임으로

$<N_{self}>_{rand} = AP_{self} = \frac {A}{N}$

표준편차는 이항분포에서 $\sigma(x) = \sqrt{npq}$ 이고, $p = \frac{1}{N}$ 이면 $q \sim 1$ 임으로

$\sigma_{rand} \approx \sqrt{\frac{A}{N}}$

만일 노드의 수가 424이고 link의 수가 519개 이면($N=424, A=519$)

$<N_{self}>_{rand} = 519 / 424 \sim 1.2$

$\sigma_{rand} = \sqrt{1.2} \sim 1.1$

실제 생물학 네트워크에서는 self-arrow의 개수가 40개 이상임으로 생물학 네트워크에서는 self-arrow가 random network에서 보다 발생할 기대값이 훨씬 큼으로 이는 임의적인 발생이 아니라, 진화과정에서 특화된, network motif라고 볼 수 있다.

2.3.1 Negative Autoregulation speeds the Response time of gene circuits.

Netative Auto regulation은 Transcription Factor(TF) X가 X 자신의 발현을 방해할 때 나타난다. (이를 NAR이라 칭하자)

Simple regulation(repressor)

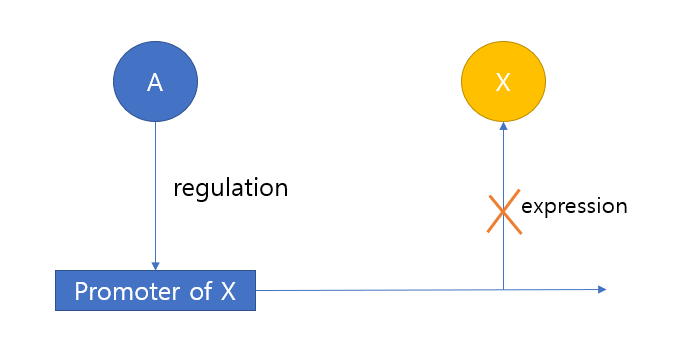
NAR

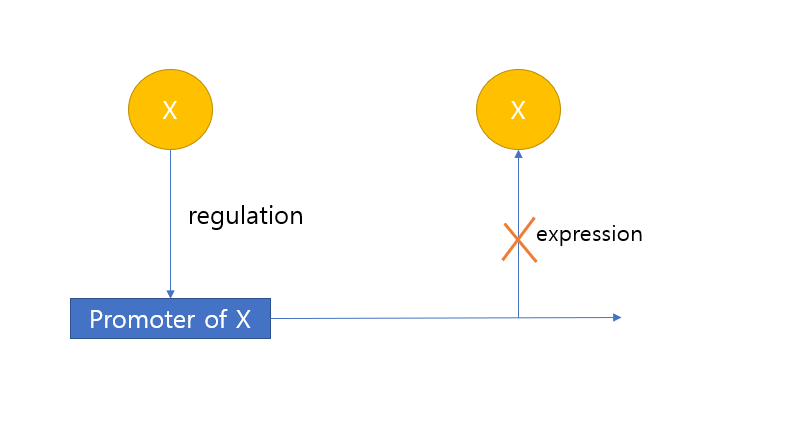
지난번 글에서 언급했듯이, $\frac{dY}{dt} = \beta - \alpha Y$임으로, Y를 X로 치환하면 $\frac{dX}{dt} = f(X) - \alpha X$ 가 된다. $\beta$가 $f(X)$가 된 것은 $f$가 repressor의 hill function으로, X의 농도에 따라 $\beta$가 결정되는 함수이기 때문이다.

$f(X) = \frac{\beta K^n}{K^N + X^N}$

좀더 직관적으로 표현하기 위해, logic approximation을 이용한다.

$f(X) = \beta\theta(X < K)$ 이에 따라 $X<K$ 일 경우 $\beta$, 그렇지 않을 경우 0이 된다.
이제 $X < K$ 일 때, 즉 $X$가 없을 경우를 가정해보자. 그럴경우 production rate는 $\beta$값이 되어 $\frac{dX}{dt} = \beta - \alpha X$가 된다.

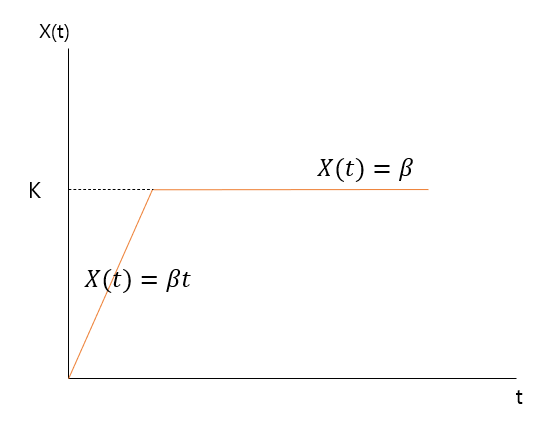
$t < \epsilon$ 이고 $\epsilon >0$ 일 때, 위의 그래프의 공식은 $X(t) = \beta t$ 가 된다.

$X(t) = \frac \beta \alpha (1 - e^{-\alpha t}) = \frac \beta \alpha (1 - (1 - \alpha t)) = \beta t$

그리고 $X = K$에 이르면 production rate이 0이되고, $X(t) = K$에 머물게 된다. 그러므로 $X_{st} = K$라는 결론이 이끌어 낼 수 있다. 이에 따라 response time은 아래와 같이 표현 될 수 있다.

$\beta T^{NAR}_{1/2} = \frac {X_{st}} 2 = \frac K 2$

$T^{NAR}_{1/2} = \frac {K} {2 \beta}$

즉, NAR의 response time은 simple repressor의 response time $T_{1/2} = \frac {\ln(2)} \alpha$ 여서 removal rate에 좌우되었던 것과 다르게 $\beta$에 의해 좌지우지 된다는 것을 알 수 있다. 즉, $\beta$가 커짐에 따라, 더욱 빠르게 response time에 도달한다는 것을 의미한다.

2.4.1 Rate Analysis Shows Speedup for Any Repressive Input Function $f(X)$

사실 $f(X)$를 반드시 logic approximation으로 하지 않아도 모든 형태의 X에 대해 감소하는 함수에서 NAR의 response time이 빨라진다.

먼저 $\frac{dX}{dt} = \beta - \alpha X 인 일반적인 조절을 생각해 보자(simple regulation)

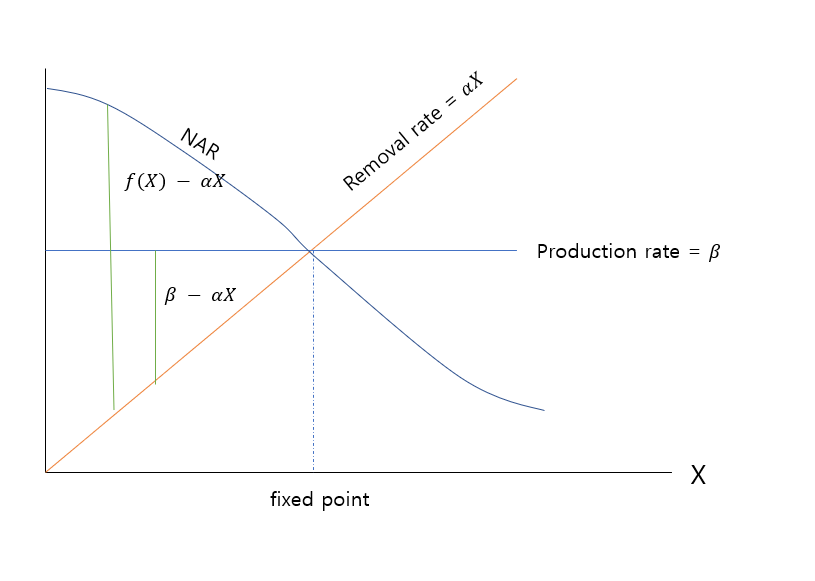
Production rate가 최대치인 $\beta$로 유지된다면, Removal Rate $\alpha X$와 만나는 지점에서 $X_{st}$가 정해지게 된다. 반면에 NAR은 어떤가? Production rate가 일정할수 없고, Production rate은 X가 증가함에 따라 자연스럽게 줄어들게 된다.

$\beta - \alpha X$가 크면 클수록, 즉 기울기가 클수록 response time에 빠르게 도달함으로, 이에, NAR은 그래프와 같이 더 큰 기울기를 가지게 되어, 빠른 response time을 가지게 된다.

2.5 NAR Promotes Robustness to Fluctuations in Production rate

어떤 셀이어서 서로 다른 $\alpha$ 값을 가지고 있더라도 NAR의 fixed point는 simple regulation에 비해 크게 변하지 않는다.

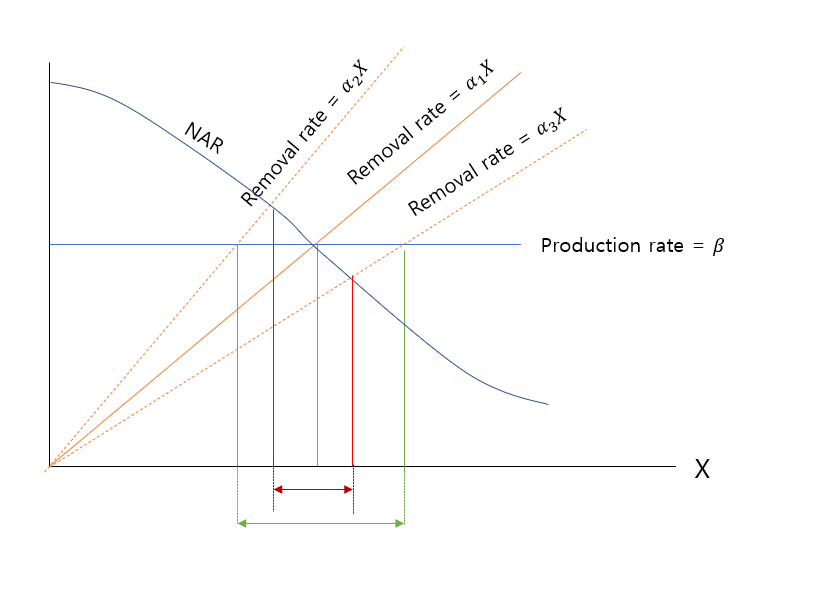
셀 1,2,3,가 있어서 서로다른 removal rate를 가진다고 했을 때, NAR와 simple regulation의 production rate와 removal rate 그래프와 만나는점을 보라. 셀 1로부터 간격이 NAR의 경우에는 좁고, simple regulation의 경우는 넓다. 즉, NAR은 $\alpha$ 값이 변경되어도, fixed point가 바뀌는 정도가 simple regulation 에 비해 작다는 것을 의미한다.