✅ DP

문제

링크

1. 문제 접근 및 해결 로직

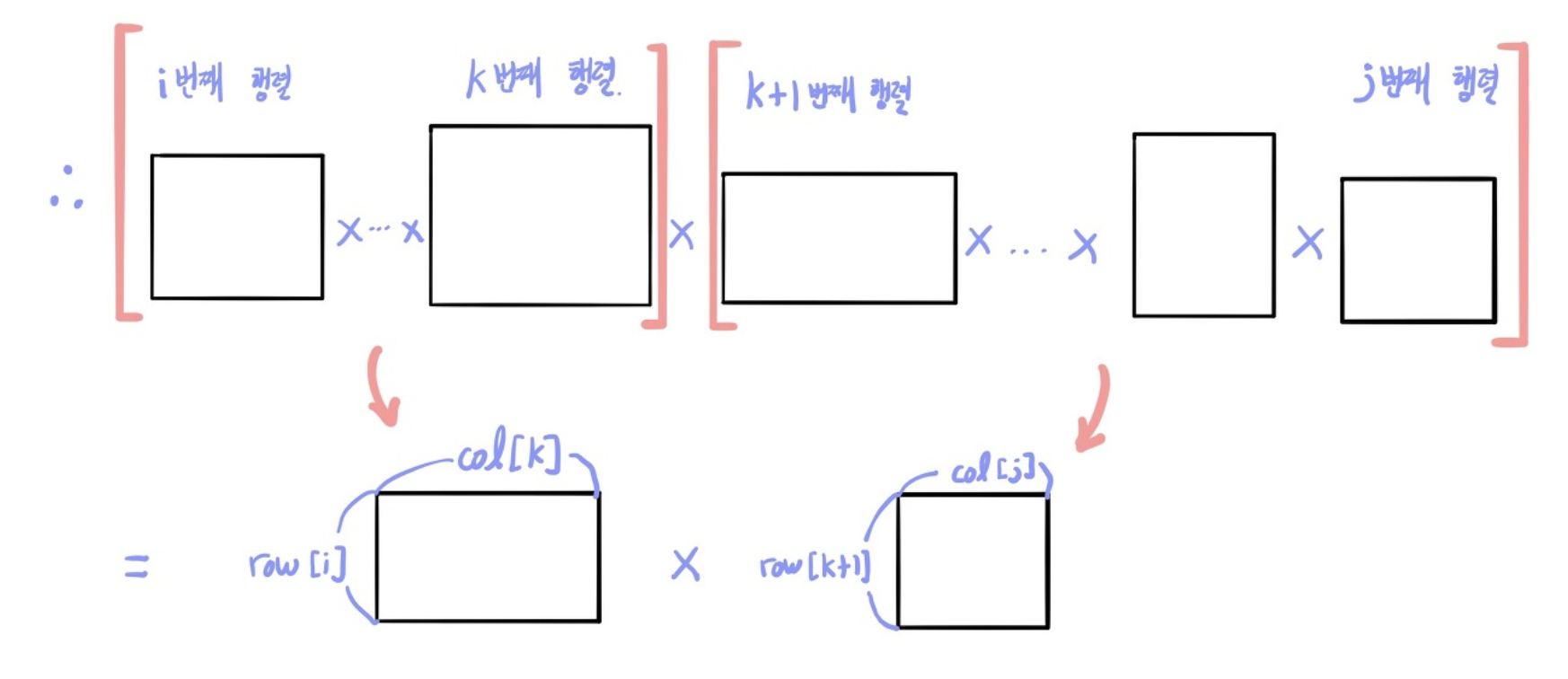
어디서 부터 어디까지 집합을 먼저 곱할지 정해져 있지 않으므로 주어진 행렬들 끼리 곱의 모든 경우를 고려해야 한다. (순서대로 곱할 수 있음)

따라서 주어진 행렬들 중에 i부터 j까지 구간의 행렬곱을 구해보자.
여기서 k가 i부터 j까지 이동한다고 하자.

(i ~ j 최소행렬 곱셈 회수) = (i ~ k 최소 병렬 곱셈 회수) + (k+1 ~ j 최소 병렬 곱셈 회수) + (i x k 행렬과 k+1 x j 행렬의 곱셈 연산의 수)

DP[i][j]를 구간 [i, j]에서의 최소 행렬 곱셈 회수라고 하여 수식으로 나타내면
$DP[i][j] = (DP[i][k] + DP[k+1][j] + row[i]*col[k]*col[j])$의 최솟값이다.

• 정의
  $DP[i][j]$ : 구간 $i,j$에서의 최소 행렬 곱셈 회수
• 구하는 답
  $DP[0][n-1]$
• 초기값
  $DP[0][0]=0$
• 점화식
  $DP[i][j] = min(DP[i][k] + DP[k+1][j] + row[i]*col[k]*col[j]),(i<=k<j,0<=i<n,j=i+len,1<=len<n)$

2. 코드

3. 시간 복잡도 분석

경우의 수를 모두 구하므로
$O(N)$

4. 문제에서 중요한 부분

DP문제는 점화식을 도출하는 것이 중요하다.
Bottm Up(반복문)으로 풀지 Top Down(재귀)으로 풀지는 선택사항