[코딩테스트] 컴공선배 - 알고리즘 캠프
1.[알고리즘] 시간/공간 복잡도
✅ big O
2.[알고리즘] 탐욕법 (greedy)

✅ 동전 거스름 문제
3.[boj] (b2) 2309 일곱 난쟁이

✅ 완전탐색
4.[boj] (s3) 3085 사탕 게임

✅ 완전탐색
5.[boj] (s3) 11047 동전 0

✅ 탐욕법 (그리디)
6.[boj] (s3) 1449 수리공 항승

✅ 그리디
7.[boj] (s5) 4673 셀프 넘버

✅ 완전탐색
8.[boj] (s4) 1065 한수

✅ 완전탐색
9.[boj] (b1) 1157 단어 공부

✅ 완전탐색
10.[boj] (b2) 1152 단어의 개수

✅ 완전탐색 ✅ getline(cin, str)
11.[boj] (b2) 2908 상수

✅ stoi()
12.[boj] (s5) 2941 크로아티아 알파벳

✅ 완전탐색
13.[boj] (s5) 1316 그룹 단어 체커

✅ 완전탐색
14.[boj] (b4) 1712 손익분기점

✅ 점화식
15.[boj] (b1) 2839 설탕배달

✅ 그리디
16.[boj] (b2) 2292 벌집

✅ 구현
17.[boj] (b1) 1193 분수찾기

✅ 구현
18.[boj] (b1) 2869 달팽이는 올라가고 싶다

✅ 구현
19.[boj] (b3) 10250 ACM 호텔

✅ 구현
20.[boj] (b1) 2775 부녀회장이 될테야

✅ 구현
21.[boj] (b4) 10162 전자레인지

✅ 그리디
22.[boj] (s5) 1439 뒤집기

✅ 그리디
23.[boj] (b3) 3053 택시 기하학

✅ 수학링크
24.[boj] (b2) 5585 거스름 돈

✅ 그리디
25.[boj] (s5) 1789 수들의 합 (미완)

✅ 그리디
26.[boj] (s5) 4796 캠핑

✅ 그리디
27.[boj] (b3) 1085 직사각형에서 탈출

✅ 구현
28.[boj] (b3) 3009 네 번째 점

✅ 구현
29.[boj] (b3) 4153 직각삼각형

✅ 구현
30.[boj] (b3) 10872 팩토리얼

✅ 재귀
31.[자료구조] 배열, 벡터, 리스트, 스택, 큐, 맵

32.[boj] (s4) 9012 괄호

✅ stack
33.[boj] (s3) 1935 후위표기식

✅ stack
34.[boj] (s4) 2164 카드2

✅ queue
35.[boj] (s1) 11286 절댓값 힙

✅ 우선순위 큐 (힙)
36.[boj] (s4) 1302 베스트셀러

✅ map
37.[boj] (s4) 1021 회전하는 큐

✅ deque
38.[boj] (s4) 1158 요세푸스 문제

✅ queue
39.[boj] (s3) 2346 풍선 터뜨리기

✅ deque
40.[boj] (s3) 1406 에디터

✅ list
41.[boj] (g3) 1918 후위표기식

✅ stack
42.[boj] (s3) 1874 스택 수열

✅ stack
43.[boj] (s4) 1764 듣보잡

✅ map
44.[boj] (s3) 10799 쇠막대기

✅ stack
45.[boj] (g4) 17298 오큰수

✅ stack
46.[boj] (s2) 2304 창고 다각형

✅ stack
47.[boj] (s1) 2841 외계인의 기타 연주

✅ stack
48.[boj] (s4) 3986 좋은 단어

✅ stack
49.[boj] (s3) 1966 프린터 큐

✅ queue ✅ priority_queue
50.[boj] (s1) 2075 N번째 큰 수

✅ priority_queue
51.[boj] (g2) 2696 중앙값 구하기

✅ priority_queue (Minheap, Maxheap)
52.[boj] (g4) 1715 카드 정렬하기

✅ priority_queue
53.[boj] (s3) 5397 키로커

✅ list
54.[boj] (s5) 7785 회사에 있는 사람

✅ map
55.[자료구조/알고리즘] 그래프, 트리, DFS, BFS

56.[boj] (s2) 11724 연결 요소의 개수

✅ 연결요소 ✅ DFS
57.[boj] (s1) 2178 미로 탐색

✅ BFS ✅ 최단거리 ✅ 문자열 배열 탐색시 인덱스 값 유의
58.[boj] (s1) 1743 음식물 피하기

✅ DFS ✅ 연결요소 ✅ DFS에서 x,y를 뒤집에서 인자로 받는 이유 ✅ 인접행렬이 아닌 이유
59.[boj] (s1) 2667 단지번호붙이기

✅ BFS ✅ 연결요소
60.[boj] (s1) 2583 영역 구하기

✅ BFS ✅ 연결요소
61.[boj] (g5) 10026 적록색약

✅ DFS ✅ 연결요소
62.[boj] (s1) 2468 안전 영역

✅ BFS ✅ 연결요소
63.[boj] (g5) 6593 상범 빌딩

✅ BFS ✅ 최단거리 ✅ queue에 struct 넣기
64.[boj] (g4) 5427 불

✅ BFS ✅ 최단거리
65.[boj] (g4) 3055 탈출

✅ BFS ✅ 최단거리
66.[boj] (g4) 2206 벽 부수고 이동하기

✅ BFS ✅ 최단거리
67.[boj] (g5) 7576 토마토

✅ BFS ✅ 최단거리
68.[boj] (s1) 7562 나이트의 이동

✅ BFS ✅ 최단경로
69.[boj] (g5) 5014 스타트링크

✅ BFS ✅ 최단경로
70.[boj] (s1) 1697 숨바꼭질

✅ BFS ✅ 최단경로
71.[boj] (g4) 16397 탈출

✅ BFS ✅ 최단경로
72.[boj] (g5) 9019 DSLR

✅ BFS ✅ 최단경로
73.[boj] (g2) 1525 퍼즐

✅ BFS ✅ 최단경로
74.[boj] (g3) 1039 교환 (미완료)

✅ 백트래킹
75.[boj] (s2) 1182 부분수열의 합

✅ DFS ✅ 백트래킹
76.[알고리즘] DP (동적계획법)

✅ 피보나치수열 ✅ 이항계수 ✅ 메모이제이션
77.[boj] (s3) 11726 2xn 타일링

✅ DP ✅ Bottom up ✅ Top down
78.[boj] (b1) 2748 피보나치 수 2

✅ DP ✅ Bottom Up ✅ long long 형
79.[boj] (s1) 11051 이항 계수2

✅ DP ✅ Top Down
80.[boj] (s1) 9465 스티커

✅ dp ✅ Bottom Up
81.[boj] (s1) 10844 쉬운 계단 수

✅ dp ✅ Bottom up
82.[boj] (b1) 2839 설탕 배달

✅ DP ✅ Bottom up
83.[boj] (s3) 9095 1,2,3 더하기

✅ DP
84.[boj] (s3) 1003 피보나치 함수

✅ DP
85.[boj] (s3) 2579 계단 오르기

✅ DP
86.[boj] (s3) 2193 이친수

✅ DP
87.[boj] (s2) 1912 연속합

✅ DP
88.[boj] (s2) 11053 가장 긴 증가하는 부분 수열

✅ DP
89.[boj] (s3) 11727 2×n 타일링 2

✅ DP
90.[boj] (s3) 9561 파도반 수열

✅ DP
91.[boj] (s3) 14501 퇴사 (미완료)

✅ DP
92.[boj] (s1) 11052 카드 구매하기

✅ DP
93.[boj] (s5) 1010 다리 놓기

✅ DP
94.[s1] (s4) 11057 오르막 수

✅ DP
95.[boj] (s3) 1904 01타일

✅ DP
96.[boj] (s2) 11722 가장 긴 감소하는 부분 수열

✅ DP
97.[boj] (g3) 11054 가장 긴 바이토닉 부분 수열

✅ DP
98.[boj] (g5) 2133 타일 채우기

✅ DP
99.[boj] (g5) 2225 합분해

✅ DP
100.[boj] (g5) 2011 암호코드 (미완료)

✅ DP
101.[boj] (s1) 11048 이동하기

✅ DP
102.[boj] (s2) 1890 점프

✅ DP
103.[boj] (s1) 1149 RGB 거리

✅ DP
104.[boj] (s1) 1932 정수 삼각형

✅ DP
105.[boj] (g5) 2293 동전 1

✅ DP
106.[boj] (g4) 1520 내리막 길

✅ DP
107.[boj] (g3) 11066 파일 합치기 (미완료)

✅ DP
108.[boj] (g3) 11049 행렬 곱셈 순서

✅ DP
109.[boj] (g4) 2228 구간나누기

✅ DP
110.[boj] (g5) 2240 자두나무

✅ DP
111.[boj] (s1) 1309 동물원

✅ DP
112.[boj] (g4) 1720 타일 코드

✅ DP
113.[boj] (s1) 1495 기타리스트

✅ DP
114.[boj] (g5) 5557 1학년

✅ DP
115.[알고리즘] 이분탐색

✅ 이분탐색 ✅ upper_bound ✅ lower_bound ✅ 매개변수 탐색
116.[boj] (s3) 2512 예산

✅ 이진탐색
117.[boj] (s4) 10815 숫자 카드

✅ 이진탐색
118.[자료구조/알고리즘] 100문제 라벨링 하기

문제 분류(=라벨링)을 하고 (ex. 그리디 / 스택 / 우선순위 큐 / 브루트포스 / DFS / 백트래킹 / 이분탐색 / 구현 등) 그 도구를 이용한 간략한 풀이 작성문제
119.[알고리즘] 구현 / 시뮬레이션

구현 / 시뮬레이션
120.[boj] (g4) 17471 게리맨더링

✅ 재귀 (or DFS) ✅ BFS
121.[boj] (g5) 파이프 옮기기 1

✅ DFS
122.[boj] (g2) 17136 색종이 붙이기

✅ DFS ✅ 백트래킹
123.[boj] (g1) 13460 구슬 탈출 2

✅ BFS ✅ 구현
124.[boj] (g5) 3190 뱀

✅ 구현 ✅ deque
125.[boj] (g2) 17143 낚시왕 (미완료)

✅
126.[boj] (g2) 12100 2048 (Easy) (미완료)

✅
127.[boj] (g4) 14499 주사위 굴리기

✅ 구현
128.[boj] (s2) 5567 결혼식

✅ 인접리스트 ✅ BFS ✅ 깊이(depth)를 세가면서 탐색
129.[boj] (s2) 6603 로또

✅ 조합 ✅ 재귀
130.[boj] (s1) 11048 이동하기

✅ DP
131.[boj] (s2) 6236 용돈 관리

✅ 이분탐색
132.[boj] (g5) 5582 공통 부분 문자열

✅ DP
133.[boj] (g1) 5214 환승

✅ BFS ✅ 중복되는 간선 (메모리초과 문제 해결 방법)
134.[boj] (g2) 1655 가운데를 말해요

✅ 우선순위큐
135.[boj] (s2) 10819 차이를 최대로

✅ 브루트포스 ✅ 순열(재귀)
136.[boj] (g3) 2146 다리 만들기

✅ BFS ✅ 연결요소
137.[boj] (g4) 7573 고기잡이 (미완료)

✅ https://www.acmicpc.net/problem/75735\. Reference
138.[boj] (g5) 4811 알약

✅ dp
139.[boj] (s1) 2343 기타 레슨

✅ 이분탐색
140.[boj] (g4) 2573 빙산

✅ DFS ✅ 연결요소의 수
141.[boj] (s4) 1002 터렛
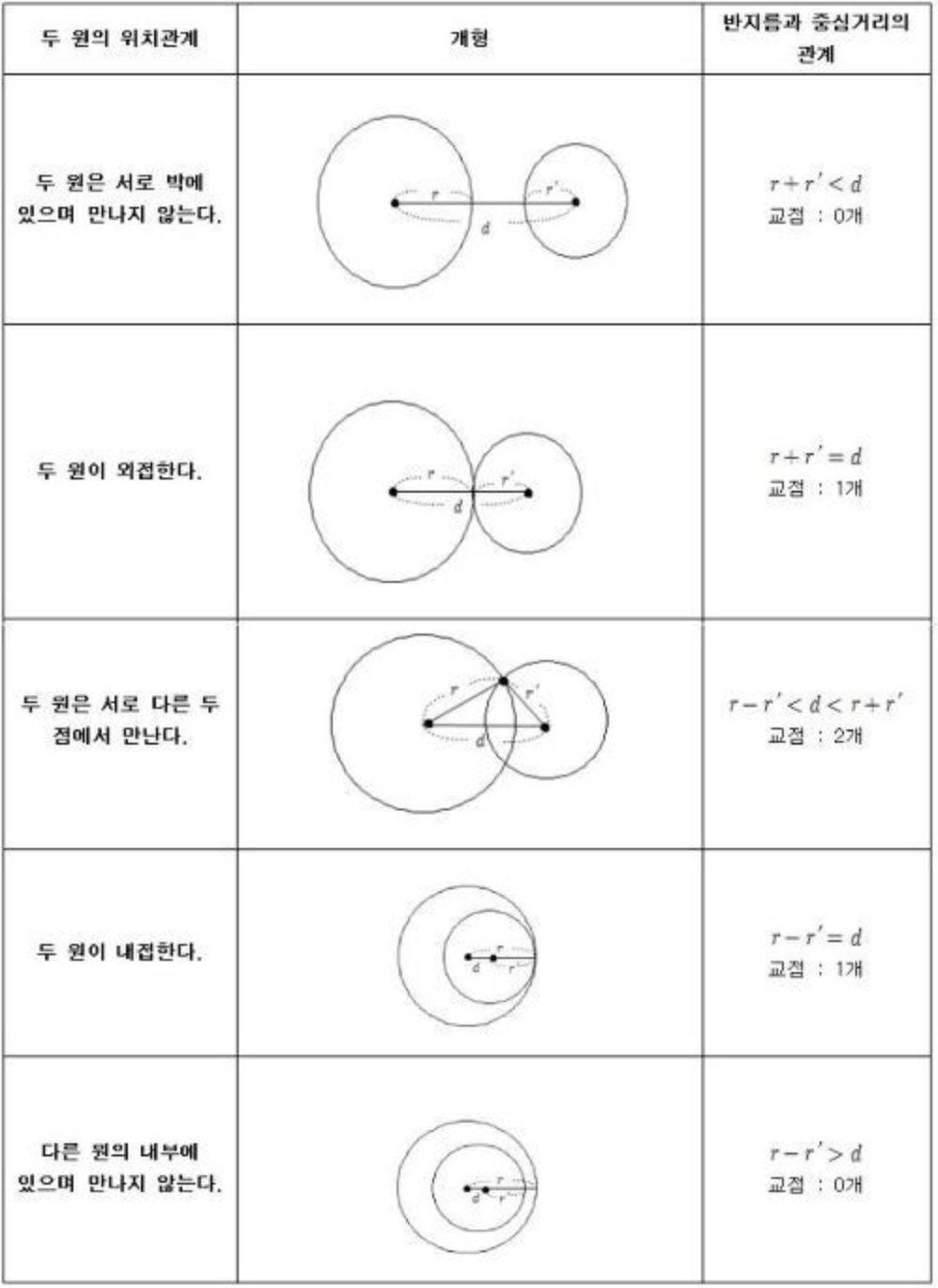
✅ 수학