✅ DP

문제

링크

1. 문제 접근 및 해결 로직

• 정의
  $dp[n]$ : 가로가 n일때 좌우 대칭 중복을 제외한 경우의 수
• 구하는 답
  $n$이 홀수 : $dp[n / 2]$
  $n$이 짝수 : $dp[n / 2]+dp[(n - 2) / 2]+dp[(n - 2) / 2]$
• 초기값
• 점화식
  $dp[i] += dp[i - 1]$
  $dp[i] += dp[i - 2] * 2$

• 점화식
  $i$에 놓을 타일은 $i - 1$ 에서 세로 타일을 놓거나
  $i - 2$에서 가로2개 or 정사각형 타일을 놓는 경우가 있다.

• 구하는 답
  N이 4일 때, 타일의 모든 경우는 다음과 같다.
  

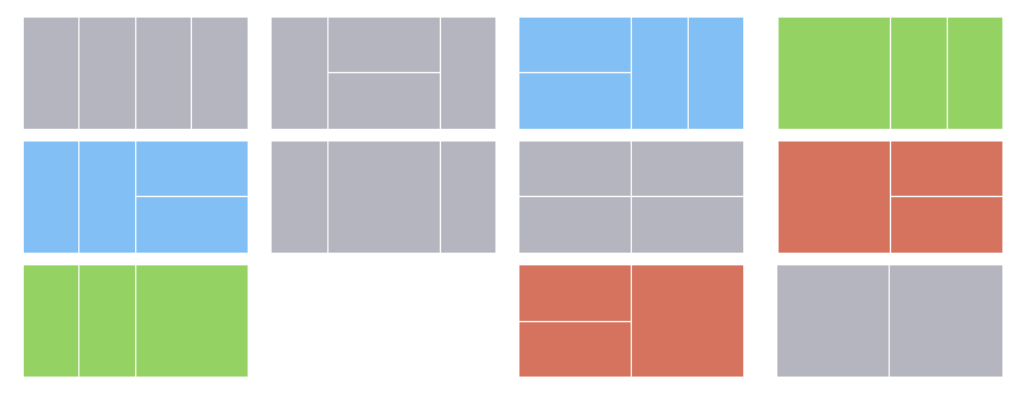
1. 좌우 대칭(색칠된 타일)인 타일 : X
2. 좌우가 같은 타일 : Y
   이라고 하면 총 2X+Y 개의 타일이 만들어진다.

좌우 대칭인 타일은 중복을 제거하여 하나의 경우 취급하기 때문에 좌우 대칭인 타일을 중복 제거 해줘야 한다. 하지만 모든 좌우 대칭인 타일(X)은 따로 규칙성이 없기 때문에 구하기 쉽지 않다. (N=4인 경우는 몇개 안되지만 N이 클수록 그 경우는 너무 많아 일일이 셀 수가 없다.)
따라서 역발상으로 좌우가 같은 타일(Y)을 구하여 총 타일 개수에 더해준 다음 2로 나누면된다.
((2X+Y)+Y)/2 = X+Y (<- 구하고자 하는 값)

그럼 이제 좌우가 같은 타일들을 구해보자.

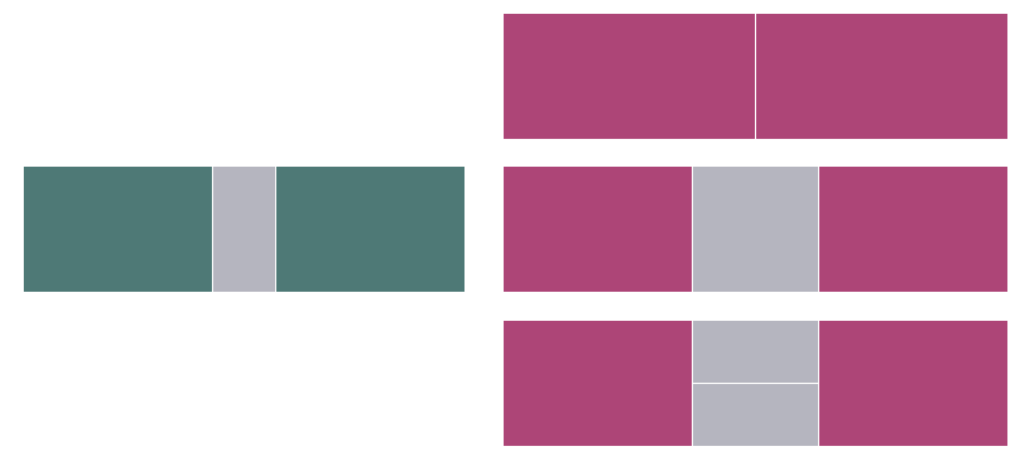
• 홀수인 경우 (초록)

위에서 n이 짝수(4)인 경우로 식을 만들었으므로 n이 짝수일 경우를 구해야
역발상으로 좌우가 같은 타일(Y)을 구하여 총 타일 개수에 더해준 다음 2로 나누는 방법을 사용할 수 있다.
((2X+Y)+Y)/2 = X+Y

따라서 가운데 세로 칸 하나를 없다고 생각하여 짝수n에서 좌우 대칭 중복을 제외한 경우의 수를 구한다
$dp[n / 2]$

• 짝수인 경우 (핑크)
  • 그냥 좌우대칭 : $dp[n / 2]$
  • 정사각형 하나 중간에 둔 경우 : $dp[(n - 2) / 2]$
  • 가로로 누인 세로막대기 * 2인 경우 : $dp[(n - 2) / 2]$

https://beginthread.tistory.com/145
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jhc9639&logNo=221805614819

2. 코드

3. 시간 복잡도 분석

경우의 수를 모두 구하므로
$O(N)$

4. 문제에서 중요한 부분

DP문제는 점화식을 도출하는 것이 중요하다.
Bottm Up(반복문)으로 풀지 Top Down(재귀)으로 풀지는 선택사항