✅ DP
문제

1. 문제 접근 및 해결 로직
벽의 크기 : 3xn
사용 가능한 타일 : 2x1, 1x2
-
벽의 크기는 최소한 홀수가 되면 안된다. 왜냐하면 2칸짜리 타일 두가지를 사용하여 채워야 하기 때문에 벽의 크기가 홀수가 되면 벽을 모두 채울 수 없다.
벽의 크기가 홀수가 되는 경우는 n이 홀수인 경우이다. -
타일의 최대 가로 길이가 2 이므로 다른 문제들에서 풀던대로 n-2에서 n으로 벽을 확장했다고 생각해보자 그럼 3x2 벽을 채울 수 있는 경우는 총 3가지 이다.

-
하지만 여기서 추가로 생각해줘야 할 경우가 있다.
벽의 세로가 3이라서 생기는 상황인데, n-4에서 n으로 벽을 확장한다고 생각해보자.
그럼 3x4 벽을 채울 수 있는 경우는 총 11가지이다.
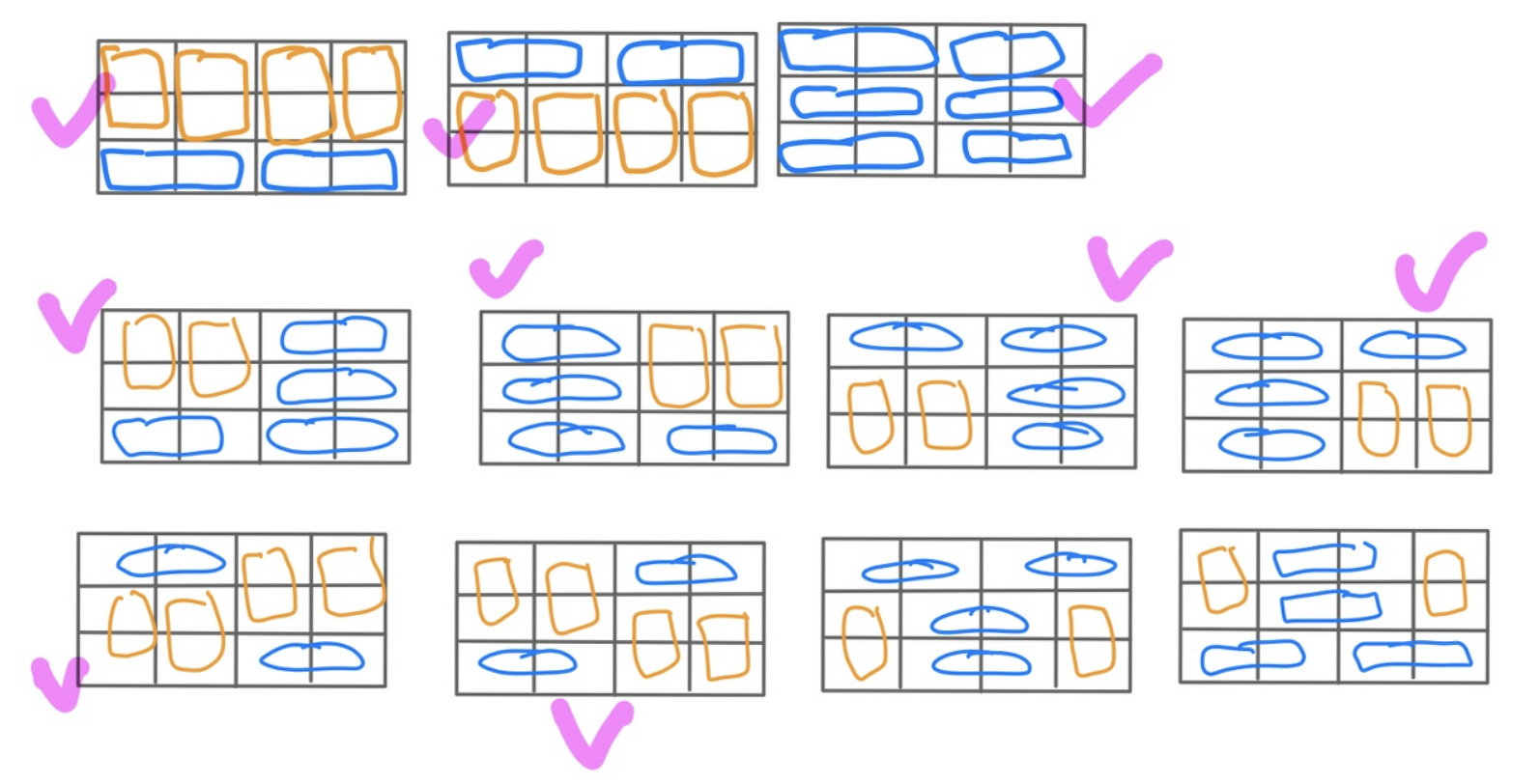
여기서 체크 되어 있는 경우는 n-2에서 커버가 되는 경우들이지만 아래 두가지 경우는 커버가 되지 않는다. 따라서 n-4 부터는 2가지 경우를 추가로 세어줘야 한다.
n-3,n-4,n-5,n-6,...
하지만 다행인 것은 n이 홀수일 경우는 만들 수 없다고 했으므로 n-3,n-5,...들은 세지 않는다. 왜냐하면 n이 짝수이므로 n-3,n-5,...은 홀수가 된다. 따라서 이경우도 만들 수 있는 경우가 없다.
정리하면 n-2 만 3가지를 추가해주고 n-4부터 짝수들은 2가지를 추가로 세어준다.
참고 : https://dlog0518.tistory.com/40
- 정의
: n에서 만들 수 있는 경우의 수- 구하는 답
- 초기값
- 점화식
(n%2==1) :
(n%2==0) :
2. 코드
3. 시간 복잡도 분석
경우의 수를 모두 구하므로
4. 문제에서 중요한 부분
DP문제는 점화식을 도출하는 것이 중요하다.
Bottm Up(반복문)으로 풀지 Top Down(재귀)으로 풀지는 선택사항
