✅ DFS ✅ 연결요소 ✅ DFS에서 x,y를 뒤집에서 인자로 받는 이유 ✅ 인접행렬이 아닌 이유

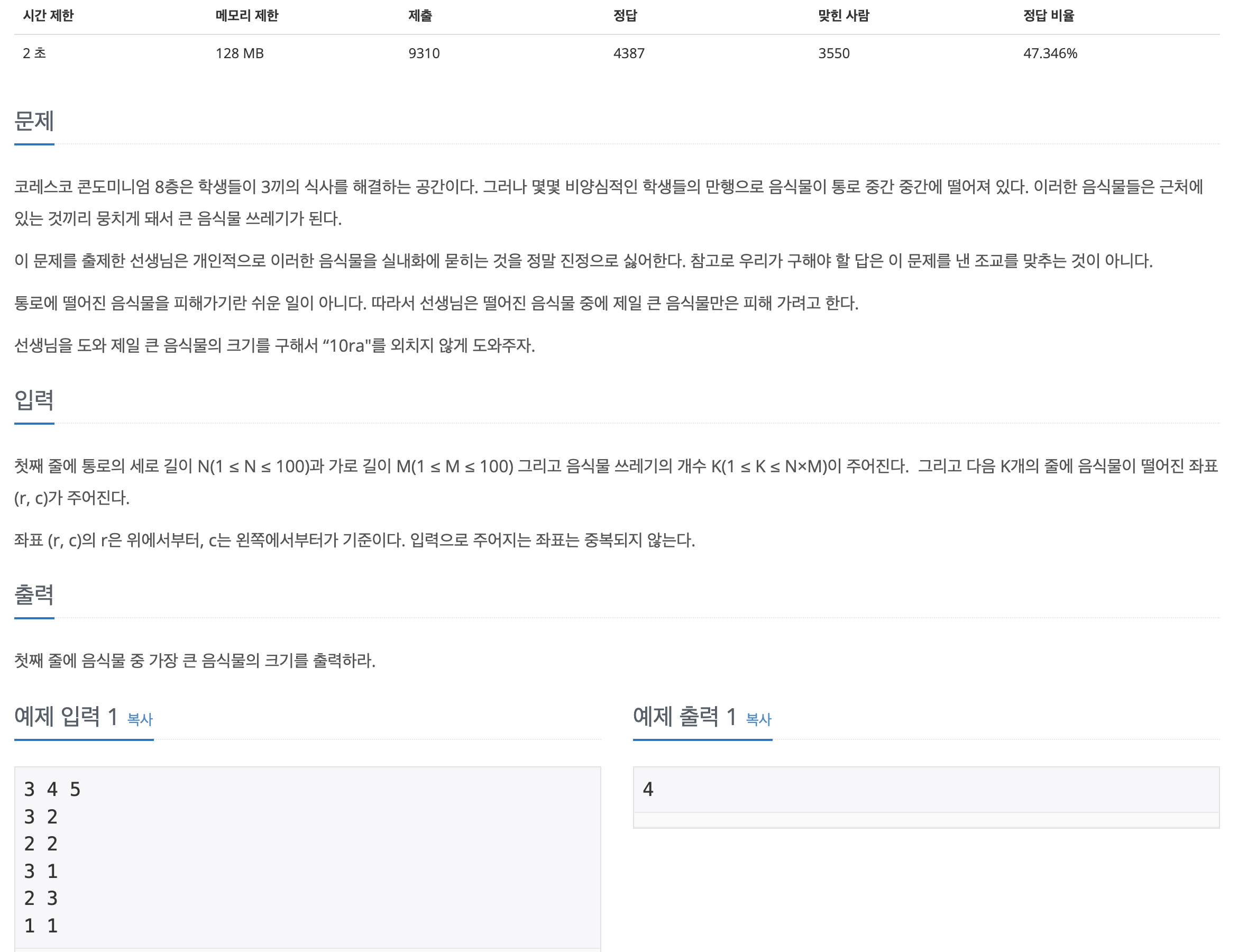
문제

링크

풀이

1. 문제 접근

• 쓰레기가 뭉칠 수 있는 방향, 즉 그래프에서 이동 가능한 방향은 상하좌우
• 인접한 쓰레기들끼리 뭉친다고 했으므로 가장 큰 쓰레기의 크기를 찾기 위해서는 인접한 크기가 가장 큰 연결요소를 찾아 그 크기를 구해야 한다.

2. 자료구조 or 알고리즘 선택과 그 이유

연결요소를 찾는 방법은 DFS, BFS 모두 가능 하지만 개인적으로 DFS가 코드상 더 간결한거 같아 DFS를 사용했다.

3. 문제 해결 로직 (풀이법)

DFS 재귀함수가 한번 돌 때 연결요소 하나를 돈 것과 같으므로 재귀함수를 돌 때마다 연결요소 크기를 구하고 그중 가장 큰 값이 구하고자 하는 값이다.

• 참고로 DFS에서 x,y를 뒤집에서 인자로 받는 이유는
  • 배열에서
    x좌표를 위에서 아래로, y좌표를 왼쪽에서 오른쪽으로 넣어줬지만
  • 좌표에서는
    x좌표가 왼쪽에서 오른쪽으로, y좌표는 아래에서 위로 가기 때문이다.(배열에 x좌표 넣을때 부호가 커질수록 아래로 넣었으므로 좌표에서 아래에서 위로 간다고 해서 부호가 바뀌진 않음)

코드

#include <iostream>
#include <algorithm>
#include <string>
#include <vector>

using namespace std;

int N, M, K; // 세로 길이 N, 가로 길이 M, 음식물 쓰레기의 개수 K
int r,c; // 좌표 (r,c)
int trash_size=0, max_size=0; // 음식물 크기
bool map[102][102];
bool visited[102][102];

int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};

void DFS(int y, int x){
    trash_size++;
    visited[y][x] = true;

    for(int i=0;i<4;i++){
        int nx = x + dx[i];
        int ny = y + dy[i];

        if(nx < 1 || ny < 1 || nx > M || ny > N) continue;

        if (map[ny][nx] == true && visited[ny][nx] == false)
        {
            DFS(ny, nx);
        }
    }
}


int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    cin >> N >> M >> K;
    for(int i=0;i<K;i++){
        cin >> r >> c;
        map[r][c] = true;
    }

    for(int i=1;i<=N;i++){
        for(int j=1;j<=M;j++){
            if (map[i][j] == true && visited[i][j] == false)
            {
                trash_size = 0;
                DFS(i, j);
                max_size = max(max_size, trash_size);
            }
        }
    }

    cout << max_size << "\n";

    return 0;
}

4. 시간 복잡도 분석

dfs는 완전탐색으로 인접 행렬을 통해 모든 좌표를 탐색했으므로
O(N*M)
(N : 좌표 세로 길이, M : 좌표 가로 길이)

즉, O(n^2)
(n : 정점의 수)

인접행렬이 아닌 이유

이문제는 인접행렬로 볼 수 없다. 왜냐하면 음식물들의 연결 관계를 이차원 배열로 나타낸게 아니라 음식물의 위치 자체를 맵에 찍어두고 탐색을 했기 때문이다.
만약 인접행렬로 푼다면 각 칸을 하나하나 정점으로 보고 0번에서부터 NM-1 번까지 넘버링을 해서 연결 관계를 표시해야 한다.
이경우 정점은 총 NM개이므로
시간복잡도는 O(NM^2) 이 된다.

5. 문제에서 중요한 부분

근처에 있는 쓰레기들끼리 뭉칠 수 있다는 것은 연결되어 있다는 뜻으로,
연결 요소를 찾는 것이라는 걸 아는 게 중요했다.