✅ 피보나치수열 ✅ 이항계수 ✅ 메모이제이션

DP

동적계획법 - Dynamic Programming (이름이랑 로직이랑 전혀 관계가 없다 😅)

문제를 쪼개서 작은 문제의 답을 구하고, 그걸로 더 큰 문제의 답을 구하는 걸 방법

• 분할정복과 비슷한 느낌
• 점화식을 구하고 재귀나 반복문을 통해 구현

유형1) 피보나치 수열

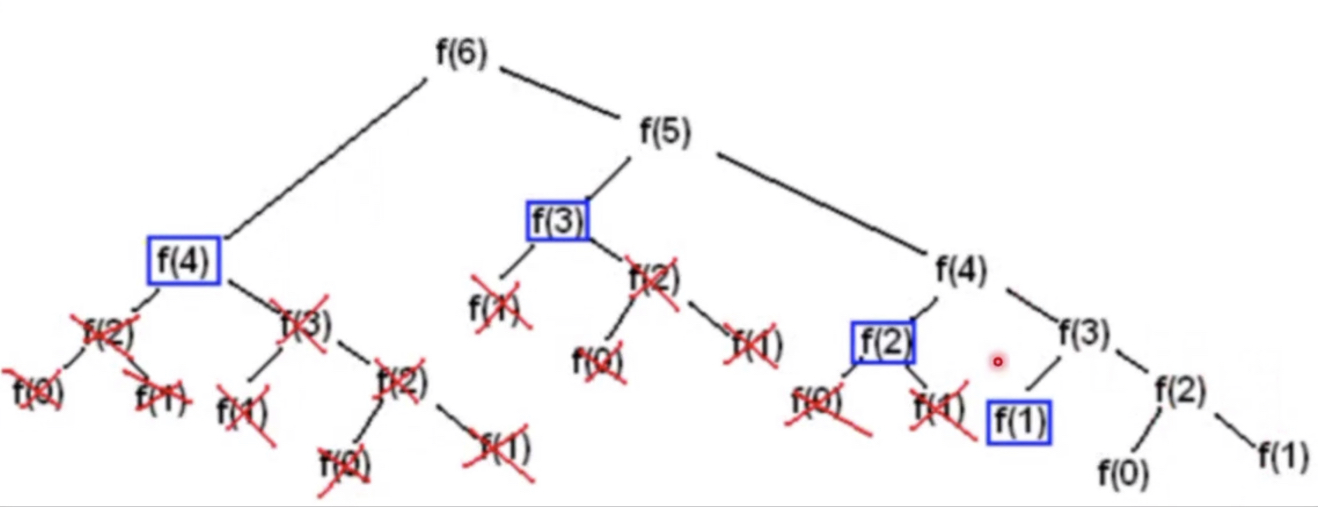
f(0)  = 0
f(1) = 1
f(n) = f(n-1) + f(n+2)

재귀함수 또는 반복문을 통해 풀 수 있다.

메모이제이션

재귀로 풀 경우
이미 구한 값을 또 구해야 하는 문제가 발생한다.

따라서 구한 값들을 저장해가며 문제를 풀어야 한다. (캐싱, 메모이제이션)
그결과 아래처럼 이전에 구한 값들을 꺼내 사용하기 때문에 중복되는 연산 (이미 구한 값)을 하지 않아도 되므로 연산 속도를 높일 수 있다.

DP 구현 방법

Top-down	Bottom-up
재귀	반복문
메모이제이션	타뷸레이션
그때그때 적어놨다가 필요한 것만 뽑아 사용	미리 다 구해놓기
직관적이라 코드 가독성이 좋다	시간과 메모리를 아낄 수도 있다
재귀함수 호출을 많이 해서 느릴 수 있다	DP테이블 채워 나가는 순서를 알아야 한다

python 의 경우 언어 자체가 느리기 때문에 둘 중에 특정 방법으로만 풀리는 경우가 있다.
c++ 은 언어 자체가 빠르기 때문에 둘중 아무거나 사용해도 됨
다만 DP테이블 채워 나가는 순서를 아는 경우에는 Bottom-up이 편함

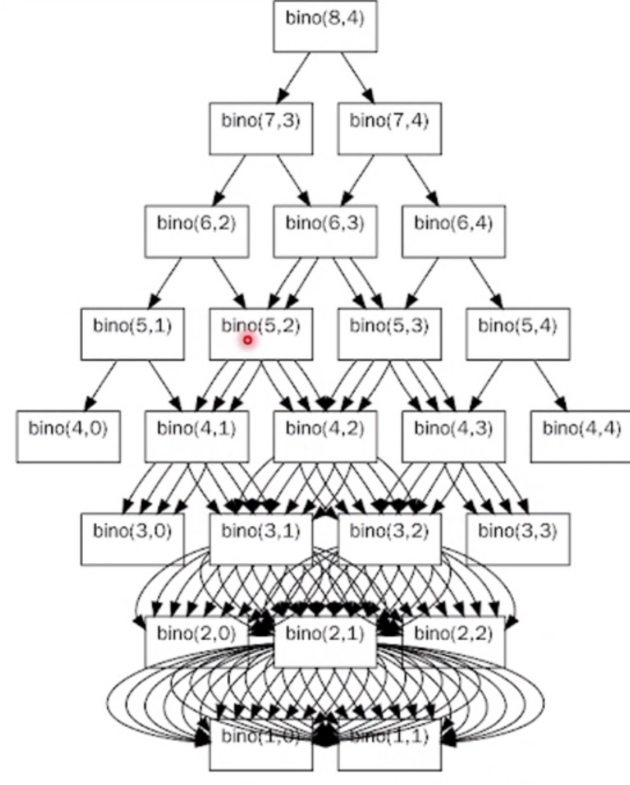
유형2) 이항계수

bino(n,0) = 1
bino(n,n) = 1
bino(n,r) = bino(n-1, r-1) + bino(n-1, r)