이분탐색

탐색 범위를 절반씩 줄여 나가는 알고리즘
반드시 정렬되어 있는 상태에서만 사용 가능하다

• $O(logN)$

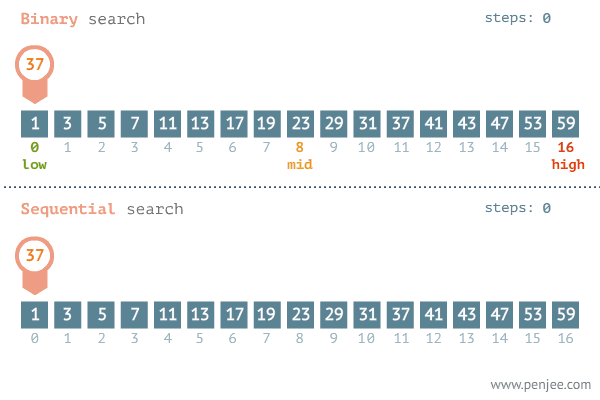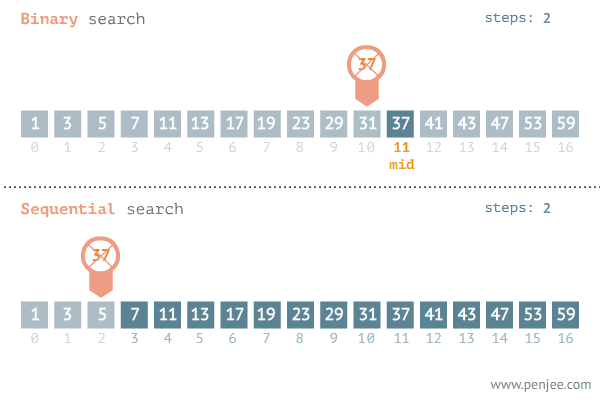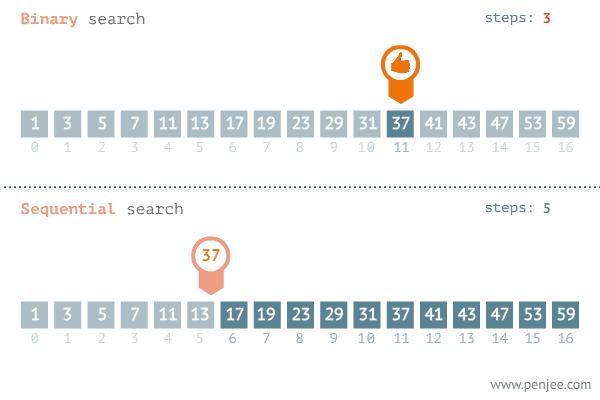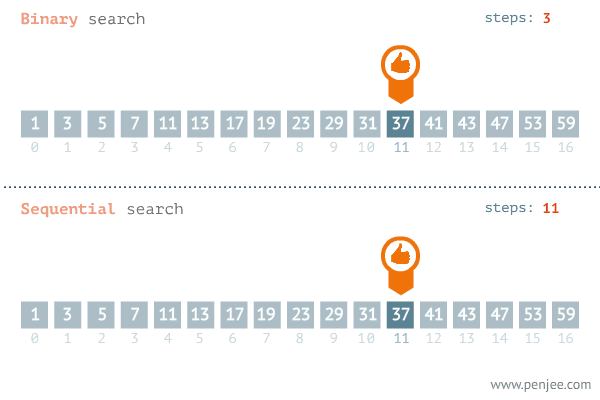
정렬을 한번 해줘야 하는 경우에는
정렬:$O(NlogN)$ + 이분탐색$O(logN)$ = $O(NlogN)$

upper_bound

lower_bound

upper_bound(begin,end,target) : target보다 큰 첫번째 요소의 주소
lower_bound(begin,end,target) : target보다 작거나 같은 첫번째 요소의 주소

• 헤더 : algorithm
• 리턴값 : 주소

- 배열에서 target 의 개수를 구하는 방법

print("%d",upper_bound(begin,end,target)-lower_bound(begin,end,target))

- 시간복잡도

• 일반 선형 탐색(반복문)으로 target의 수를 찾는다면 : $O(N)$
• 이진탐색(upper_bound, lower_bound) 사용 : $O(logN)$

매개변수 탐색

Parametric Search

최적화 문제를 결정문제(true,false)로 하여 이분탐색으로 푸는 방법

• 매개변수가 주어지면 true or false가 결정되어야 한다.
• 가능한 해의 영역이 연속적이어야 한다.
  • true였다가 false였다가 true 였다가 이러면 안됨, 경계값은 1개만 있어야 함
  • 정렬되어 있어야 한다고 생각하면 됨
• 범위를 반씩 줄여가면서 가운데 값이 true인지 false인지 구하고 그에 따라 다음 살펴볼 쪽 범위를 구한다.