[U-stage] Week 1.

Pear_Mh·2021년 8월 14일

Boostcamp_Ustage

목록 보기

1/1

강의 복습!

DL-Basic의 1강부터 10강까지 수강하고 필수과제 작성 및 해당 내용들을 제가 구축한 DL-framework에 맞추어 연습했습니다. 해당 부분은 추후에 개별적으로 올릴 예정입니다!

강의 정리(예)

## (01강) 딥러닝 기본 용어 설명 - Historical Review

### 01. 딥러닝 기본 용어 설명
#### 딥러닝 개발자의 필수 역량
  1. 구현 능력
  2. 선형대수, 확률에 대한 수학적 지식
  3. 최근 연구에 대한 지식

#### 딥러닝의 필수 요소

#### 01) Data
  - Ex.
    - Classification(분류)
    - Semantic Segmentation(분리)
    - Detection(검출)
    - Pose Estimation(추정)
    - Visual Q&A
    ...

  Cf) **의료 영상 분석**에서는 
      - Classification, Segmentation, Enhancement, Registration가 중요하다!
    
#### 02) Model
  - 데이터를 어떻게 변형시켜 원하는 문제를 해결할 지
  - Ex. 
    - AlexNet
    - GoogleNet
    - ResNet
    - DenseNet
    - LSTM
    - Deep AutoEncoders
    - GAN
    - ...
    
#### 03) Loss function
  - 데이터를 토대로 산출한 모델의 예측값과 실제값의 차이를 표현하는 지표
  - Ex.
    - Regression Task
    - Classification Task
    - Probabilistic Task
    ...
#### 04) **Optimization algorithm** : Adjust the parameters to minimize the loss
  - 손실을 최소화하기 위한 매개변수를 조정
  - Ex.
    - Dropout - For reducing overfitting in artificial neural networks by preventing complex co-adaptations on training data
    - Early stopping
    - k-fold validation
    - Weight decay
    - Batch normalizaion
      ...

### 02. Historical Review

#### 1. AlexNet(2012)
- Convolution Neural Network
- 244 x 244 image classifiaction

#### 2. DQN(2013)
- Reinforcement learning
- Q-learning
  
#### 3. Encoder/Decoder(2014)
- To solve Neural Machine Translation(NMT)
  
#### 4. Adam Optimizer(2014)
  
#### 5. Generative Adversarial Network(2015)
- Generator / Discriminator learning
  
#### 6. Residual Networks(2016)
- Solve **overfitting** problem while stack lot of network
  
#### 7. Transformer(2017)
- paradigm shift
  
#### 8.BERT(2018)
- Fine-tuned NLP models
  
#### 9.Big Language Model(GPT-X)(2019)
- autoregressive language model with 175 billion parameters
  
#### 10.Self supervised learning(2020)
- Using unsupervised learning

---

## (02강) Neural Networks & Multi-Layer-Perceptron

## Neural Networks

### 01. Introduction

**"Neural networks are computing system vaguely inspired by the biological neural networks that constitute animal brains."**

- Neural networks are **function approximators** that **stack affine transformations** followed by **nonlinear transformations**.

### 02. Linear Neural Networks

#### Ex) Linear Regression
- Data: $\mathcal{D} = \{(x_i,y_i)\}_{i=1}^N$ (x: 1D, y: 1D)
- Model: $\hat{y} = wx + b$
- Loss: $loss = {1 \over N}\sum_{i=1}^N (y_i-\hat{y_i})^2$

**We compute the partial derivatives w.r.t the optimization variables.**

$$
{\partial_{loss} \over \partial_{w}} that Partial derivative
={\partial \over \partial_w}{1 \over N}\sum_{i=1}^N (y_i-\hat{y_i})^2
={\partial \over \partial_w}{1 \over N}\sum_{i=1}^N (y_i-wx_i-b)^2
=-{1 \over N}\sum_{i=1}^N -2(y_i-wx_i-b)^2x_i
$$
**Then, we iteratively update optimization variables**

  Update  $w, b$ and stepsize $\eta$
  
  $w \leftarrow w - \eta{\partial{loss} \over \partial{w}}$
  $b \leftarrow b - \eta{\partial{loss} \over \partial{b}}$

**Of course, we can handle multi dimensional input and output**

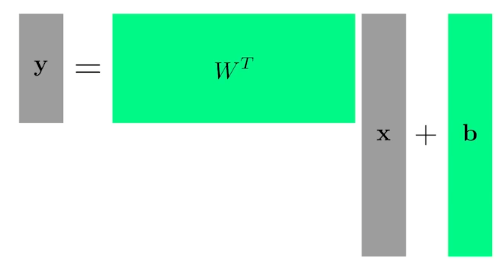
  ![](https://velog.velcdn.com/images%2Fpear_min%2Fpost%2Fd73c2492-45b7-4031-95e6-84e140701498%2Fimage.png)

  $$
  y=W^Tx+b
  $$
  
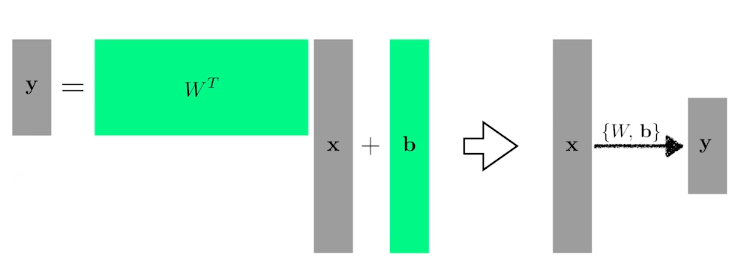
  ![](https://velog.velcdn.com/images%2Fpear_min%2Fpost%2Fa1da9e6c-a6d1-4a70-a788-3f02f75910bf%2Fimage.png)
  
  One way of interpreting a matrix is to regard it as a mapping between two vector spaces
    
### 03. Beyond Linear Neural Networks 

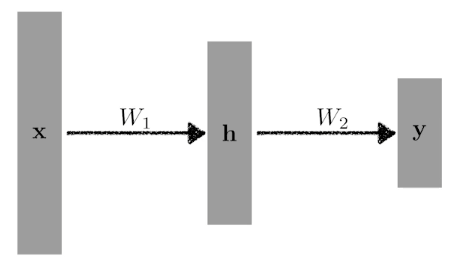
  ![](https://velog.velcdn.com/images%2Fpear_min%2Fpost%2Fa08612e6-e68b-4f99-915c-268019679de7%2Fimage.png)
  
  $$
  y = W_2^Th=W_2^TW_1^Tx
  $$
  $$W_2^TW_1^T$$ just means **another matrix** so, we need nonlinear transform **$\rho$**.

  $$
  y = W_2^Th=W_2^T\rho(W_1^Tx)
  $$

#### Activation functions

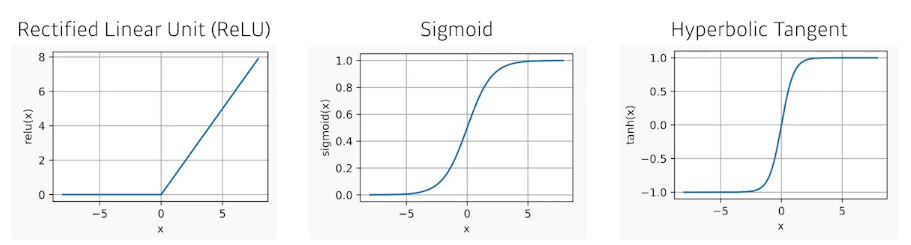
  ![](https://velog.velcdn.com/images%2Fpear_min%2Fpost%2F17221143-cfb4-4640-a656-174bbf68db38%2Fimage.png)

  - Relu: $$R(x)=x^{+}=\max(0,x)$$
  
  - Sigmoid: $S(x)={1 \over {1+e^{-1}}}={e^x\over{e^x+1}}$
  
  - Tanh: $tanh x={e^x-e^{-x}\over {e^x+e^{-x}}}={e^{2x}-1\over e^{2x}+1}$

## Mult-Layer Perceptron

### 01. Introduction

**This class of architectures are often called multi-layer perceptrons.**

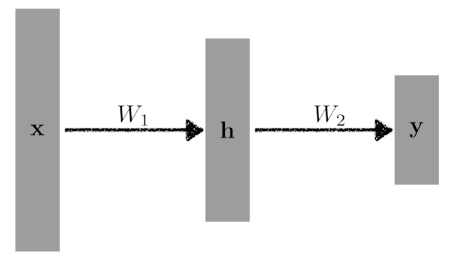
  ![](https://velog.velcdn.com/images%2Fpear_min%2Fpost%2F61a4274a-979d-4e69-82cc-4f3e64d8cef4%2Fimage.png)

  $$
  y = W_2^Th=W_2^T\rho(W_1^Tx)
  $$

#### Loss function
  
  - Regression Task : $MSE={1 \over N}\sum_{i=1}^N\sum_{d=1}^D(y_i^{(d)}-\hat{y_i^{(d)}})^2$
    - $y_i^{(d)}$: True target
    - $\hat{y_i}^{(d)}$: Predicted output

  - Classification Task : $CE=-{1 \over N}\sum_{i=1}^N\sum_{d=1}^Dy_i^{(d)}\log\hat{y_i}^{(d)}$

  - Probabilistic Task : ${1 \over N}\sum_{i=1}^N\sum_{d=1}^Dy_i^{(d)}\log\mathcal N(y_i^{(d)};\hat{y_i}^{(d)},1)$ (=MSE)
  
## (03강) Optimization