[2주차 Day2] 03강: LU분해

노션 기록

행렬 분해(matrix decomposition)의 의미

인수분해의 행렬버전이라고 생각하면 쉬움

어떤 수를 인수분해한 상태로 가지고 있으면 분수의 약분, 두 수의 최대공약수/최소공배수 구하기 등의 계산에서 유리함 → 행렬의 경우도 마찬가지

대표적인 행렬분해

• $LU$분해 ($LU$ decomposition)
• $QR$분해 ($QR$ decomposition)
• 특이값 분해(SVD, Sigular Value Decomposition)

$QR$분해와 특이값분해는 직교분할과 관련된 내용으로 이후 다룰 예정.

LU 분해(LU decomposition)

LU분해란?

$LU$분해는 주어진 행렬을 아래의 형태를 가지는 두 행렬의 곱으로 나누는 행렬분해이다

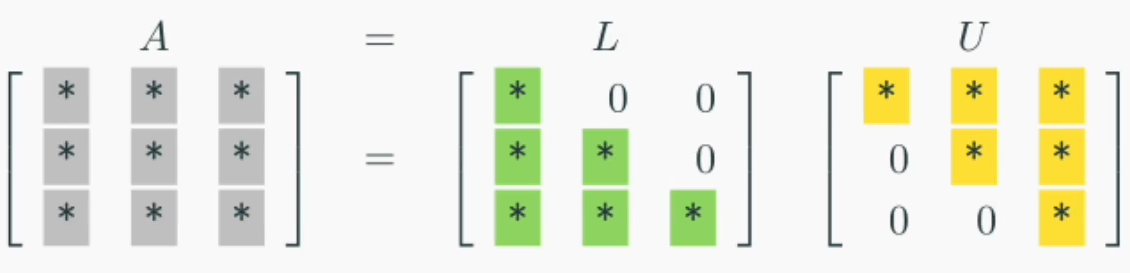
행렬 $L$과 $U$는 그 형태를 따라 다음과 같이 불린다

• $L$ : lower triangular matrix (하삼각행렬)
• $U$ : upper triangular matrix (상삼각행렬)

LU 분해의 장점

$LU$분해를 이용해 $A\rm x=b$ 문제를 아래와 같이 나타내면,

선형시스템을 다음과 같이 두 단계로 간단히 해결할 수 있다 :

LU 분해의 의미

$LU$분해는 가우스 소거법의 forward elimination(전방소거법)을 행렬로 코드화 한 것

$A = PLU$

• $L$ : 행렬 $A$를 전방소거하는데 쓰인 replacement와 scaling에 대한 EROs를 기록해 둔 행렬
• $U$ : 행렬 $A$를 전방소거한 후 남은 upper triangular matrix(상삼각행렬)
• $P$: 행렬 $A$를 전방소거하는데 쓰인 interchange에 대한 EROs를 기록해 둔 행렬(옵션)

$LU$ 분해는 가우스 소거법의 전방소거법과 의미가 거의 같음

LU 분해의 활용

$A$의 역행렬 $A^{-1}$을 구하면 될 것 같은데 왜 굳이 $LU$ 분해를 쓰는 걸까?

• 수치적 안정성

  • 선형시스템 $A \rm x = b$의 해를 역행렬 $A^{-1}$을 이용해 직접 구하는 것 보다 $PLU$ 분해를 이용하는 것이 좀 더 수치적으로 안정적이다

• $\rm b$가 자주 업데이트 되는 경우

  • 선형시스템 $A \rm x = b$에서 행렬 A는 고정되어 있고 $\rm b$가 자주 변하는 문제가 종종 있다
  • 이런 경우, 행렬 $A$를 미리 $PLU$로 분해해 둔다면, $\rm b$가 업데이트 될 때마다 선형시스템의 해 $\rm x$를 실시간으로 구할 수 있다