노션 기록
선형시스템 Ax=b 의 해
- 해가 하나인 경우(unique solution)
- 3x=6
- [1−231][x1x2]=[23]
- 해가 없는 경우(no solution)
- 0x=6
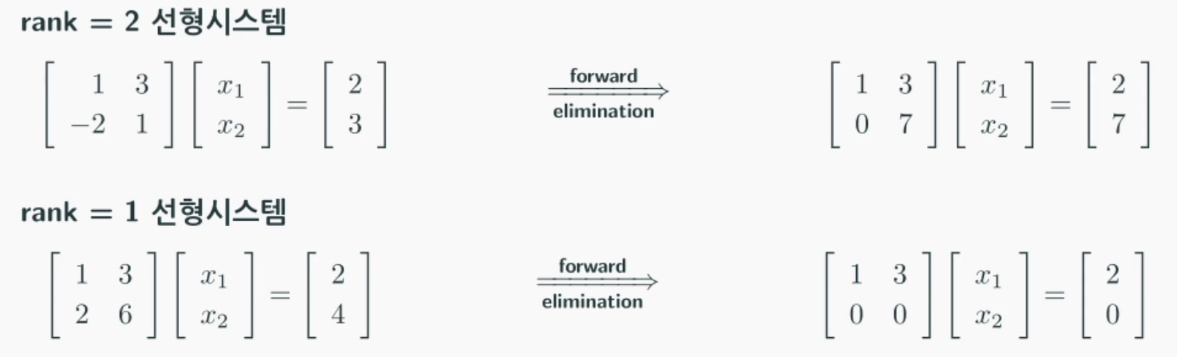
- [1236][x1x2]=[25]
- 해가 여러개인 경우(infinitely many solutions)
- 0x=0
- [1236][x1x2]=[24]
- a=0이면 특이하다
- ax=b (a,b 는 scalar)의 해가 곧장 나오지 않는다. 왜?
- a의 역수(inverse)가 존재하지 않는 경우 a가 특이(singular)하다고 한다.
- A가 행렬인 경우 역행렬(inverse matrix)이 존재하지 않으면 A가 특이하다고 한다.
- 해가 있으면 선형시스템이 consistent하다고 한다.
- 해가 없으면 선형시스템이 inconsistent하다고 한다.
가우스 소거법(Gauss elimination)
가우스 소거법은 임의의 m×n 선형시스템의 해를 구하는 가장 대표적인 방법이다
가우스 소거법의 두 단계
가우스 소거법은 다음 두 단계로 수행된다 :
-
Forward elimination(전방소거법) ⭐
주어진 선형시스템을 아래로 갈수록 더 단순한 형태의 선형방정식을 가지도록 변형한다
-
주어진 선형 시스템
⎣⎢⎡∗∗∗∗∗∗∗∗∗⎦⎥⎤⎣⎢⎡x1x2x3⎦⎥⎤=⎣⎢⎡∗∗∗⎦⎥⎤
-
Forward elimination(전방소거법) 수행 후
⎣⎢⎡∗00∗∗0∗∗∗⎦⎥⎤⎣⎢⎡x1x2x3⎦⎥⎤=⎣⎢⎡∗∗∗⎦⎥⎤
전방소거법을 수행하면 마지막 행을 초등교과수준의 가장 단순한 선형방정식으로 만들 수 있다!
-
Back-substitution(후방대입법)
아래에서부터 위로 미지수를 실제값으로 대체하여 선형시스템의 해를 구한다
-
Forward elimination(전방소거법) 수행 후
⎣⎢⎡100210131⎦⎥⎤⎣⎢⎡x1x2x3⎦⎥⎤=⎣⎢⎡151⎦⎥⎤
-
Back-substitution(후방대입법) 수행 후
⎣⎢⎡100210131⎦⎥⎤⎣⎢⎡−421⎦⎥⎤=⎣⎢⎡151⎦⎥⎤
후방대입법을 수행할 때 아래에서부터 위로 풀어나가는 각 선형방정식은 초등교과수준의 방정식이다!
-
예제
-
주어진 선형 시스템
⎣⎢⎡11222313−1⎦⎥⎤⎣⎢⎡x1x2x3⎦⎥⎤=⎣⎢⎡13−3⎦⎥⎤
E1:x1+2x2+x3=1E2:x1+2x2+3x3=3E3:2x1+3x2−x3=−3
-
전방소거법
-
후방대입법
-
x3=1
⎣⎢⎡100210131⎦⎥⎤⎣⎢⎡x1x21⎦⎥⎤=⎣⎢⎡151⎦⎥⎤
-
x2=2
⎣⎢⎡100210131⎦⎥⎤⎣⎢⎡x121⎦⎥⎤=⎣⎢⎡151⎦⎥⎤
-
x1=−4
⎣⎢⎡100210131⎦⎥⎤⎣⎢⎡−421⎦⎥⎤=⎣⎢⎡151⎦⎥⎤
소거법에 쓰이는 기본행연산(Elementary Row Operations, EROs)
소거법에는 3가지 기본행연산이 있다.
-
Replacement(치환) : rj←rj−m ri
- j번째 행을 기준행인 i번째 행을 m배하여 빼서 업데이트한다
-
Interchange(교환) : rj↔ri
- j번째 행과 i번째 행의 위치를 서로 바꾼다
-
Scaling(스케일링) : rj←s rj
Forward Elimination(전방소거법)의 가치 ⭐
가우스 소거법에서 전방소거법의 가치는 다음과 같다