노션 기록

좌표계 변환(Change of Basis):

좌표계 :: 좌표값 = 행렬 :: 벡터

벡터의 표현: 고등교과과정부터 시작하기

벡터는 크기와 방향을 가진 물리량으로 다음과 같이 표현될 수 있습니다

벡터의 물리적 표현 (좌표계 없는 표현)

벡터 $\bf v$를 화살표로 표현한다

• $\bf v$의 크기 : 화살표의 길이
• $\bf v$의 방향 : 화살표의 방향

벡터의 수학적 표현 (좌표계 있는 표현)

벡터 $\bf v$를 화살표로 표현한다

좌표계를 도입한 후, 벡터의 시작점을 원점에 맞추고 끝점의 위치를 벡터 $\bf v$의 수학적 표현으로 정의한다

• $\bf v$의 크기 : 화살표의 길이를 계산
• $\bf v$의 방향 : 화살표의 방향을 벡터로 표현
  
  
  

좌표계(Coordinate System)

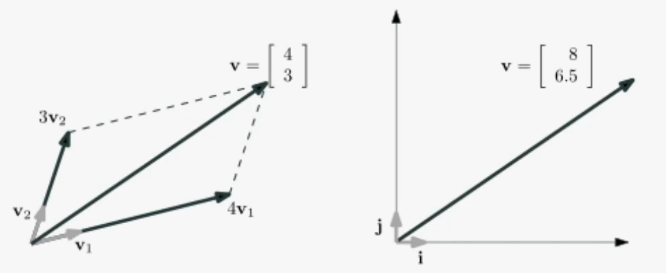
다음과 같이 2-벡터 $\bf v$가 주어졌다고 하자.

이 벡터는 $xy$-평면 상에서는 원점$(0, 0)$에서 시작하여 $(a, b)$에서 끝나는 벡터를 의미한다.

$\bf v$는 다음과 같이 해석될 수 있다 (선형조합)

즉, 수식의 각 요소는 다음과 같다

• $a \begin{bmatrix} 1\\0 \end{bmatrix}$ : $x$-축으로 내린 수선의 발. 즉, $x$-축의 단위로 $a$번 전진함
• $b \begin{bmatrix} 0\\1 \end{bmatrix}$ : $y$-축으로 내린 수선의 발. 즉, $y$-축의 단위로 $b$번 전진함
• $xy$-좌표계: $\begin{bmatrix} 1&0\\0&1 \end{bmatrix}$

• 예제

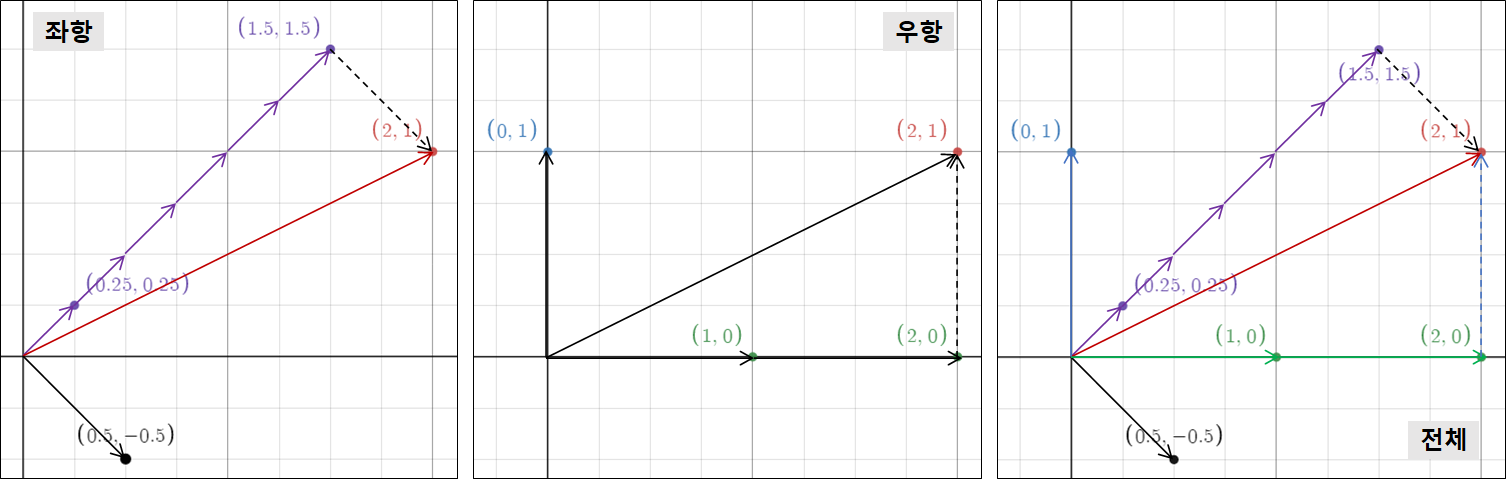
  만일 두 벡터 $\bf v_1$과 $\bf v_2$를 이용해 새롭게 좌표계를 만든다면 $\bf v$의 좌표값은 무엇일까요?

  새로운 좌표계를 만든다는 말은 어떤 벡터 $\bf v$에 도착하기까지의 과정을 오롯이 $\bf v_1$과 $\bf v_2$를 몇 번 사용하여 도착했는지로 표현한다는 의미입니다.

  즉, $\bf v_1$과 $\bf v_2$를 이용해 만든 새로운 좌표계에서 $\bf v$ 좌표값은 $(4, 3)$이라 해야합니다.

  왜냐하면,

  $4{\bf v}_1 + 3{\bf v}_2 = \bf v$

  이기 때문입니다

  

  일반적인 $xy$ 좌표계에서 $\bf v$ 좌표값은 $(8, 6.5)$임!

  지금까지의 전체과정을 행렬로 표현하면 아래와 같습니다

  $\begin{aligned} \begin{bmatrix} {\bf v}_1&{\bf v}_2 \end{bmatrix} \begin{bmatrix} 4\\3 \end{bmatrix} &= \begin{bmatrix} \bf v \end{bmatrix} \left( = \begin{bmatrix} a\\b \end{bmatrix} \right) \\ \begin{bmatrix} {\bf v}_1&{\bf v}_2 \end{bmatrix} \begin{bmatrix} 4\\3 \end{bmatrix} &= \begin{bmatrix} {\bf e}_1&{\bf e}_2 \end{bmatrix} \begin{bmatrix} a\\b \end{bmatrix} \end{aligned}$

  위 식의 (좌항)과 (우항)이 표현하는 바는 다음과 같습니다

  • 우항 :
    • ${\bf e}_1$과 ${\bf e}_2$를 기저(basis)로 가지는 표준좌표계(standard coordinate system)에서 벡터 $\bf v$의 좌표값은 $(a,b)$입니다 위의 예제에서는 $(8, 6.5)$
  • 좌항 :
    • ${\bf v}_1$과 ${\bf v}_2$를 기저(basis)로 가지는 좌표계(coordinate system)에서는 동일한 벡터 $\bf v$의 좌표값이 $(4, 3)$입니다

좌표계 변환(Change of Basis)

이제 선형시스템(linear system)문제를 좌표계 변환으로 바라보는 새로운 시선을 배웠습니다

• 우항 : 표준좌표계(standard coordinate system)에서 어떤 벡터의 좌표값은 $\bf b$이다
• 좌항 : $A$의 열벡터들을 기저(basis)로 가지는 좌표계에서 동일 벡터의 좌표값은 $\bf x$이다
  
  

  • 예

    $\begin{bmatrix} 1&-1\\2&2 \end{bmatrix} \begin{bmatrix} 2\\1 \end{bmatrix} = \begin{bmatrix} 1\\6 \end{bmatrix}$

    우항은 이렇게 다시 나타낼 수 있다

    $\begin{bmatrix} 1&-1\\2&2 \end{bmatrix} \begin{bmatrix} 2\\1 \end{bmatrix} = \begin{bmatrix} 1&0\\0&1 \end{bmatrix} \begin{bmatrix} 1\\6 \end{bmatrix}$

    즉, $(1, 6)$은 우리가 알고 있는 표준좌표계에서 어떤 벡터의 좌표값을 의미하고
    $A$의 열벡터를 기준으로 하는 좌표계에서의 좌표값은 $\bf x$인 $(2, 1)$이 되는 것!

    둘은 동일하다!!

    

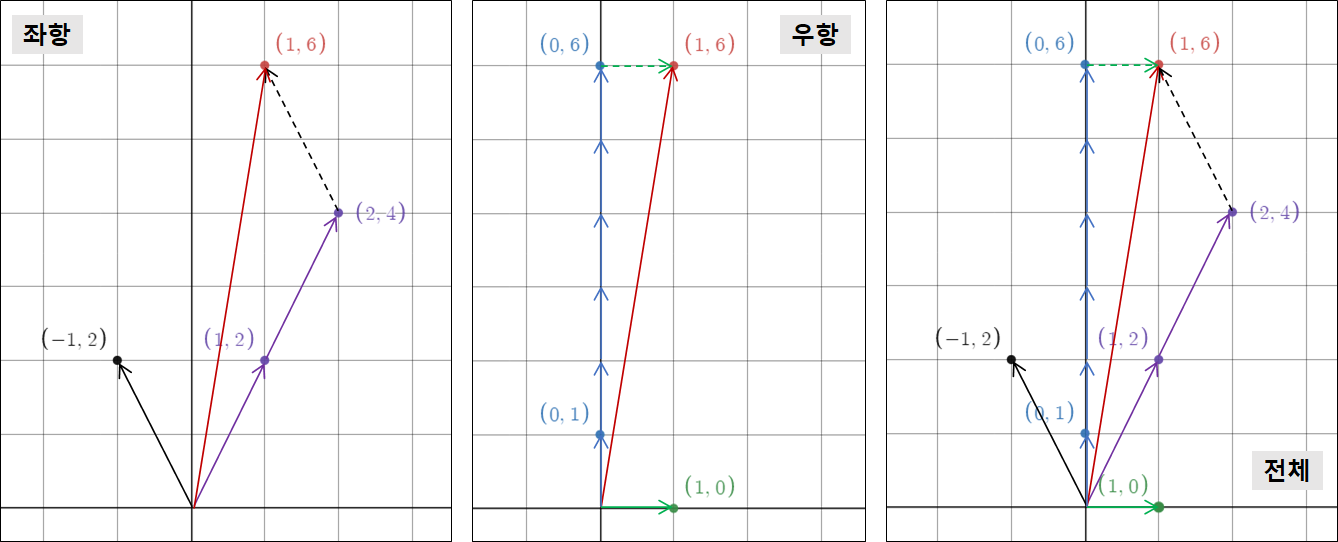
역행렬을 이용해 선형시스템의 해를 구하는 문제 역시 좌표계 변환으로 바라볼 수 있습니다

• 우항 : $A^{-1}$의 열벡터들을 기저(basis)로 가지는 좌표계에서는 동일 벡터의 좌표값은 $\bf b$이다
• 좌항 : 표준좌표계(standard coordinate system)에서 어떤 벡터의 좌표값은 $\bf x$이다

• 예

  $\begin{bmatrix} 1&-1\\2&2 \end{bmatrix} \begin{bmatrix} 2\\1 \end{bmatrix} = \begin{bmatrix} 1\\6 \end{bmatrix} \Rightarrow \begin{bmatrix} 1\over2&1\over4\\-1\over2&1\over4 \end{bmatrix} \begin{bmatrix} 1\\6 \end{bmatrix} = \begin{bmatrix} 2\\1 \end{bmatrix}$

  이때는 $(2, 1)$은 우리가 알고 있는 표준좌표계에서 어떤 벡터의 좌표값을 의미하고
  $A^{-1}$의 열벡터를 기준으로 하는 좌표계에서의 좌표값은 $\bf b$인 $(1, 6)$이 되는 것!

  관점의 차이다!!

  

정리

행렬은 좌표계이고, 벡터는 좌표값입니다

임의의 $\bf v$는 다양한 좌표계에서 표현될 수 있습니다

• 예제 문제

  예제 #1.

  2-벡터 $\bf v$가 표준좌표계에서 $(2, 3)$으로 표현된다고 합시다

  벡터$(3, 1)$과 $(1, -2)$를 기저벡터로 가지는 새로운 좌표계를 도입했을 때, 해당 벡터 $\bf v$는 어떤 좌표값을 가질까요?
  
  

  $\begin{bmatrix} 3&1\\1&-2 \end{bmatrix} \begin{bmatrix} x_1\\x_2 \end{bmatrix} = \begin{bmatrix} 2\\3 \end{bmatrix} \Rightarrow x_1 \begin{bmatrix} 3\\1 \end{bmatrix} + x_2 \begin{bmatrix} 1\\-2 \end{bmatrix} = \begin{bmatrix} 2\\3 \end{bmatrix} \quad \therefore x_1 = 1, x_2 = -1$

  
  
  

  예제 #2.

  3-벡터 $\bf v$가 표준좌표계에서 $(2, 1, 3)$으로 표현된다고 합시다

  벡터$(1, 3, 1)$과 $(1, -2, 2)$를 기저벡터로 가지는 새로운 좌표계를 도입했을 때, 해당 벡터 $\bf v$는 어떤 좌표값을 가질까요?
  
  

  $\begin{bmatrix} 1&1\\3&-2\\1&2 \end{bmatrix} \begin{bmatrix} x_1\\x_2\end{bmatrix} = \begin{bmatrix} 2\\1\\3 \end{bmatrix} \Rightarrow x_1 \begin{bmatrix} 1\\3\\1 \end{bmatrix} + x_2 \begin{bmatrix} 1\\-2\\2 \end{bmatrix} = \begin{bmatrix} 2\\1\\3 \end{bmatrix} \quad \therefore x_1 = 1, x_2 = 1$