노션 기록

함수 복습

초등/중등 교과과정부터 시작하기

Functions: A Review

초등, 중등, 고등 교과과정을 통해 함수에 관해 많은 지식을 배웠을 겁니다
하지만 막상 함수의 개념을 설명하라고 하면 쉽지 않습니다

초등 교과과정에서 배운 함수의 개념은 다음과 같습니다

함수는 상자(함)에 입력(input)이 들어가면 어떤 기능을 수행한 다음 출력을 뱉어내는 블랙박스(black box)다

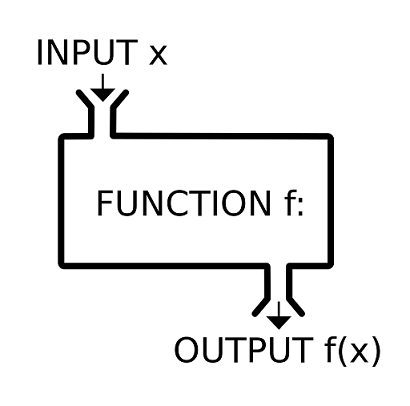
중등 교과과정에서 배운 함수의 개념이 좀 더 수학적으로 명쾌합니다

중등 교과과정에서 배운 함수의 개념은 다음과 같습니다

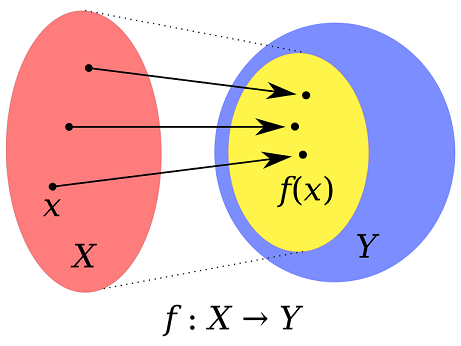
함수는 두 집합 간의 맵핑룰(mapping rule)이다

• 입력이 정의되는 집합 $X$를 domain(정의역)이라 합니다

• 출력이 정의되는 집합 $Y$를 codomain(공역)이라 하며, codomain 중 실제 함수의 출력이 나오는 부분집합은 range(치역)이라 합니다
  
  

함수 $f$는 그림과 같이 $X$의 각 원소 $x$가 $Y$의 한 원소 $y(=f(x))$에 대응되는 매핑룰(mapping rule)입니다.

실제로 함수의 수학적인 표현 ${\atop X}{f\atop \longrightarrow}{\atop Y }$ 또는 $f : X \longrightarrow Y$ 는 이러한 사실을 명확히 전달합니다

고등 교육과정에서 다음과 같은 함수를 자주 접해봤을 겁니다

이 함수는 domain과 codomain을 강조하여 다음과 같이 적을 수 있습니다

C-스타일 프로그래밍으로 해당 함수 $f$ 를 구현한다면 아래와 같을 겁니다

입출력으로 실수 집합 $\bf R$(real number)을 다루는 함수라는 것을 명시하기 위해 입출력 타입을 $\tt float$으로 지정했음을 주목하기 바랍니다

선형함수(linear function)

만일 함수 $f$가 아래 두 가지 조건을 만족하면 함수 $f$를 선형함수(linear function)이라고 합니다
(단, $c$는 임의의 스칼라)

위 식은 언뜻 보면 당연하게 보이지만, 실은 함수 $f$에 대해 전혀 당연하지 않은 성질을 설명하고 있습니다

• 임의의 두 입력에 대해 '+연산을 먼저 수행한 결과를 함수 입력으로 넣고 함수를 수행한 결과'와 '각 입력에 대해 함수를 수행한 후 나온 결과에 대해 +연산을 수행한 결과'는 같다

• 임의의 입력에 대해, '스칼라 곱셈 연산을 먼저 수행한 다음 함수를 수행한 결과'와
  '입력에 대해 함수를 수행한 후 나온 결과에 대해 스칼라 곱셈연산을 수행한 결과'는 같다
  
  
  
  

선형변환(linear transformation)

행렬은 선형변환의 구현체

변환(Transformation)

함수의 입력이 $n$-벡터이고 출력이 $m$-벡터인 함수 $T$를 생각해 봅시다.

이와 같이 함수의 입출력이 벡터인 함수를 변환(transformation)이라 합니다

특별히 $n=m$인 경우, 해당 변환을 연산자(operator)라고 합니다

• 변환의 예 : MNIST 손글씨 인식 문제

  예를 들어, $28 \times 28$ 해상도의 손글씨 숫자 영상을 그레이스케일로 받아, 0부터 9까지의 어떤 숫자가 적혀있는지 알아내는 MNIST 손글씨 인식 문제는 다음과 같은 (비선형)변환입니다

  $T:{\bf R}^{28 \times 28} \longrightarrow {\bf R}^{10}$

행렬변환(Matrix Transformation)

$m \times n$ 행렬 $A$에 대해 $A \bf x$는 $n$-벡터를 입력으로 받아 $m$-벡터를 출력으로 내는 변환 $T_A({\bf x}) = A{\bf x}$으로 볼 수 있습니다.

이 변환은 행렬이 정의하기 때문에 행렬변환(Matrix Transformation)이라고 합니다.

그런데 행렬변환은 다음의 선형함수 성질을 모두 만족하기 때문에 선형변환(linear transformation)입니다 (단, ${\bf x, y \in R}^n$이고, $c$는 임의의 스칼라)

정리

$m \times n$ 행렬은 $n$-벡터를 입력으로 받아 $m$-벡터를 출력으로 내는 선형변환이며, 임의의 선형변환은 행렬로 표현가능하다

즉, 행렬은 선형변환의 구현체입니다

이 세상의 모든 행렬은 선형변환이다! → 선형변환을 행렬로 표기하여 코딩 가능하다!!!

표준행렬(standard matrix)

선형변환 코딩하기

행렬변환 코딩하기

행렬변환이 입출력이 벡터로 정의된 선형함수라면, 해당 함수를 어떻게 코딩할 수 있을까?
우리가 원하는 방식대로 동작하는 행렬변환을 코딩하는 방법이 무엇일까?

다음 절차를 통해 우리가 원하는 방식대로 동작하는 행렬변환을 코딩할 수 있다

1. 구현하고자 하는 기능(function)의 입력과 출력이 벡터로 정의되는지 확인한다

2. 구현하고자 하는 기능이 선형인지 확인한다

3. 입력이 $n$-벡터이고, 출력이 $m$-벡터이면 $m \times n$ 표준행렬(standard matrix)을 구성한다
   
   
   
   

표준행렬(Standard Matrix)을 이용한 선형변환 코딩

다음의 $m \times n$ 표준행렬(standard matrix)을 구성함으로써, 우리가 원하는 방식대로 동작하는 행렬변환 $T_A:{\bf R}^n \longrightarrow {\bf R}^m$을 코딩할 수 있다.

정리: 표준행렬 구하기

• $n$-차원 표준기저벡터 $\{e_1, e_2, \cdots, e_n\}$를 생각한다 각 축($n$)에 대한 결과들을 생각한다!

• 각 $n$-차원 표준기저벡터 $e_i$에 대해, 우리가 원하는 기능을 동작시켜 얻은 결과인 $m$-차원 벡터 $T(e_i)$를 표준행렬의 각 열에 적는다

• 예제 문제

  예제 #1.

  2차원 벡터를 입력으로 받아, 해당 벡터를 $x$-축에 프로젝션하는 기능을 구현해보자.

  먼저 판단할 사항:

  1. 이 문제가 변환인가?
     → 입력과 출력이 벡터로 정의되므로 변환이다!
     
     

  2. 이 문제가 선형 변환인가? (선형 함수인가?)
     → 직선을 넣었을 때 직선이 나오므로 선형이다!

     이 문제는 선형변환 문제이므로 $m \times n$ 표준행렬(standard matrix)을 구성한다!

     답 : $\begin{bmatrix} 1&0\\0&0 \end{bmatrix}$

  
  

  예제 #2.

  2차원 벡터를 입력으로 받아, 해당 벡터를 반시계방향으로 $\theta$만큼 회전하는 기능을 구현해보자.

  먼저 판단할 사항:

  1. 이 문제가 변환인가?
     → 입력과 출력이 벡터로 정의되므로 변환이다!
     
     

  2. 이 문제가 선형 변환인가? (선형 함수인가?)
     → 직선을 넣었을 때 회전을 해도 결과가 직선이 나오므로 선형이다!

     이 문제는 선형변환 문제이므로 $m \times n$ 표준행렬(standard matrix)을 구성한다!

     답 : $\begin{bmatrix} cos\theta&-sin\theta\\sin\theta&cos\theta \end{bmatrix}$