노션 기록

벡터에 대한 고찰

고등 교과과정부터 시작하기


$n$-벡터는 크기와 방향을 가진 물리량으로 다음과 같이 표현될 수 있습니다

좌표계 없이 표현

• $\bf v$ : 화살표로 표현
• $\bf v$의 크기 : 화살표의 길이 측정
• $\bf v$의 방향 : 화살표의 방향 측정
  
  

좌표계를 도입하여 표현

• ${\bf v} = (v_1, v_2, \cdots, v_n)$
• $\bf v$의 크기 : $\Vert{\bf v}\Vert = \sqrt{v^2_1+v^2_2+\cdots+v^2_n}$
• $\bf v$의 방향 : ${1\over\Vert{\bf v}\Vert}\bf v$

벡터의 내적(Inner product)

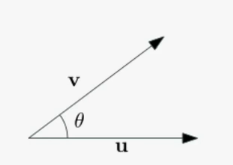
두 벡터 $\bf u$와 $\bf v$에 대한 내적(inner product 혹은 dot product)는 다음과 같이 정의된다.


좌표계 없이 표현

두 $n$-벡터의 길이와 두 벡터 간의 사이각 $\theta$을 통해 다음과 같이 정의된다

${\bf u \cdot v = \Vert u\Vert \Vert v\Vert} \cos\theta$


좌표계를 도입하여 표현

${\bf u} = (u_1, u_2, \cdots, u_n)$, ${\bf v} = (v_1, v_2, \cdots, v_n)$의 좌표값을 통해 다음과 같이 계산된다

${\bf u \cdot v} = u_1v_1 + u_2v_2 + \cdots + u_nv_n$

두 벡터 $\bf u, \bf v$간의 내적이 0이면 두 벡터는 직교(orthogonal)이다

직교의 물리적 의미

${\bf u \bot v}$일 때, ${\bf u}$ 방향으로의 전진은 ${\bf v}$ 방향에서 전혀 측정되지 않는다. 그 반대도 마찬가지이다.

** 고교 과정에서 배운 $xy$-좌표계나 $xyz$-좌표계가 직교좌표계였음을 상기하도록 하자
서로가 독립적이다!

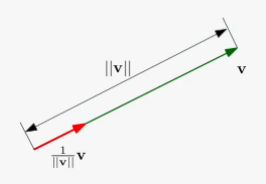
벡터의 투영(Projection)

두 벡터 $\bf u, a$가 있을 때, 벡터 $\bf u$를 $\bf a$위에 투영한 벡터를 $\rm proj\bf_a u$ 라 하고 다음과 같이 구한다

• 길이

  • 투영한 벡터 $\rm proj\bf_a u$의 길이는 $\bf \Vert u \Vert\cos\theta$

  • ${\bf u \cdot a = \Vert u\Vert \Vert a\Vert} \cos\theta$ 이므로,

  • $\bf \Vert u \Vert\cos\theta = {\bf u \cdot a \over \Vert a\Vert}$
    
    

• 방향

  • 투영한 벡터 $\rm proj\bf_a u$의 방향은 a의 방향과 일치하므로 a의 방향을 구한다

  • 즉, $\bf{ 1 \over \Vert a \Vert} \Vert a \Vert$

스칼라와 벡터를 분리해서 적으면, $\bf \left({u \cdot a \over \Vert a \Vert^2} \right)a$ 가 되고, 스칼라 값은 벡터 $\bf a$에 대한 스케일 값이 된다.

벡터 $\bf u$를 $\bf a$위에 투영하고 남은 보완 벡터(complement vector)는 $\bf u - \rm proj\bf _a u$ 이다

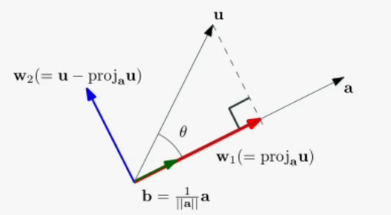
중요한 점은 투영한 벡터와 보완벡터가 서로 직교한다는 것임!!
즉, 투영을 통해 두 벡터를 직교분할 할 수 있음!

벡터의 직교분해(Orthogonal Decomposition)

두 벡터 $\bf u, a$가 있을 때, 투영과 보완의 개념을 이용해 직교분할 할 수 있다

직교행렬(Orthogonal Matrix)

직교좌표계에 대한 행렬 표현

직교행렬(Orthogonal Matrix)이란?

행렬은 좌표계라는 의미를 이미 배웠다.

즉, 행렬은 각 열벡터가 기저(basis)를 이루는 좌표계(coordinate system)이다

직교행렬(orthogonal matrix)

주어진 행렬의 모든 열벡터가 서로 직교한다면(내적 = 0), 이 행렬을 직교행렬이라 한다

직교행렬은 직교좌표계를 의미한다

정규직교행렬(orthonormal matrix)

주어진 행렬이 직교행렬이고 모든 열벡터의 크기가 1이라면 이 행렬을 정규직교행렬이라 한다

정규직교행렬은 정규직교좌표계를 의미한다

정규직교행렬을 회전행렬(rotation matrix) 이라고도 함
(x, y축을 회전시켜 놓은 것으로 생각할 수 있기 때문)

직교행렬(Orthogonal Matrix)을 이용한 선형시스템

선형시스템 $A\bf x= b$에서 행렬 $A$가 직교행렬(orthogonal matrix)이면, 해(solution) $\bf x$는 역행렬 $A^{-1}$의 계산 없이 다음과 같이 구할 수 있다

• $\bf x$의 $i$-번째 요소는 투영(projection)으로 계산할 수 있다.

  • 즉, 벡터 $\bf b$를 행렬 $A$의 각 열벡터 ${\bf a}_i$에 투영한 연산 ${\rm proj} {\bf a}_i \bf b$로부터 $x_i = {{\bf b \cdot a}_i\over \Vert{\bf a}_i \Vert ^2}$임을 계산할 수 있다.

• $\bf x$의 $i$-번째 요소와 $j$-번째 요소의 계산은 독립적이다.

  • 즉, $\bf x$의 계산은 병렬처리 가능하다

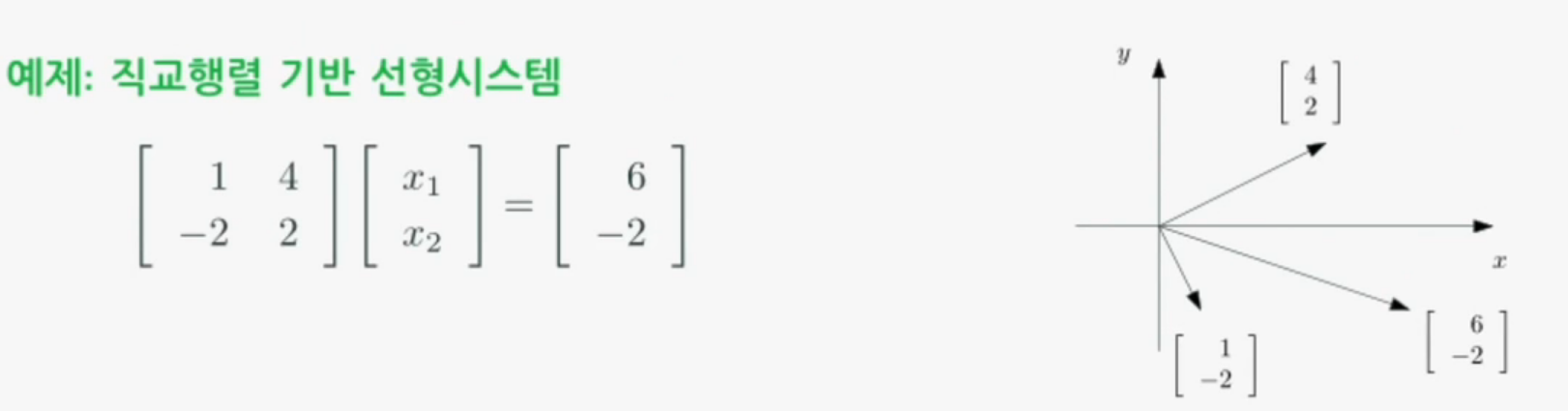
정규직교행렬(Orthonormal Matrix)을 이용한 선형시스템

선형시스템 $A\bf x= b$에서 행렬 $A$가 정규직교행렬(orthonormal matrix)이면, 해(solution) $\bf x$는 역행렬 $A^{-1}$의 계산 없이 다음과 같이 구할 수 있다

• $\bf x$의 $i$-번째 요소는 내적(inner product)으로 계산할 수 있다.

  • 정규직교행렬은 열벡터의 크기가 1이므로!

  • 즉, 벡터 $\bf b$를 행렬 $A$의 각 열벡터 ${\bf a}_i$에 투영한 연산 ${\rm proj} {\bf a}_i \bf b$로부터 $x_i = {\bf b \cdot a}_i$임을 계산할 수 있다.

• $\bf x$의 $i$-번째 요소와 $j$-번째 요소의 계산은 독립적이다.

  즉, $\bf x$의 계산은 병렬처리 가능하다

QR 분해 : A = QR

주어진 행렬에서 정규직교행렬 추출

행렬분해(matrix decomposition)의 의미

주어진 행렬을 행렬분해된 상태로 가지고 있으면 여러모로 계산이 편한 경우가 많습니다

다음은 대표적인 행렬분해입니다

• $LU$분해 ($LU$ decomposition)
• $QR$분해 ($QR$ decomposition)
• 특이값 분해(SVD, Sigular Value Decomposition)
  
  
  

QR분해 (QR decomposition)

$QR$분해는 주어진 행렬을 아래의 형태를 가지는 두 행렬의 곱으로 나누는 행렬분해입니다

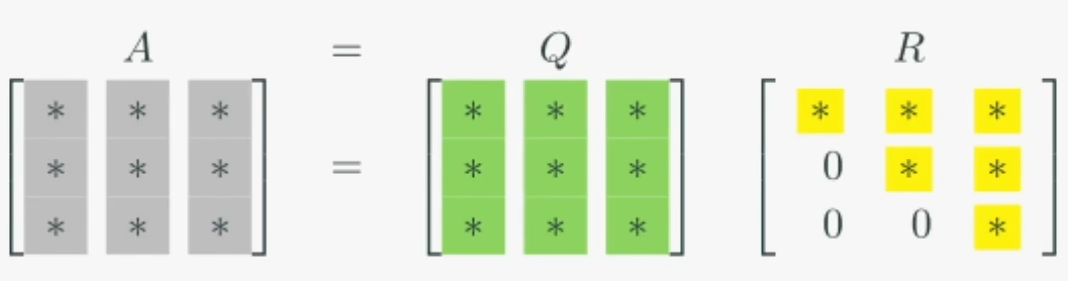
행렬 $Q$와 $R$은 그 특성에 따라 다음과 같이 불립니다

• $Q$ : 정규직교행렬(orthonormal matrix)
• $R$ : 상삼각행렬(upper traingular matrix)
  
  
  

주어진 행렬 $A$가 $QR$분해되어 있으면 무엇이 장점일까요?

$QR$분해를 이용해 $A \bf x = b$ 문제를 아래와 같이 나타내면,

선형시스템을 다음과 같이 두 단계로 간단히 해결할 수 있음을 알 수 있습니다

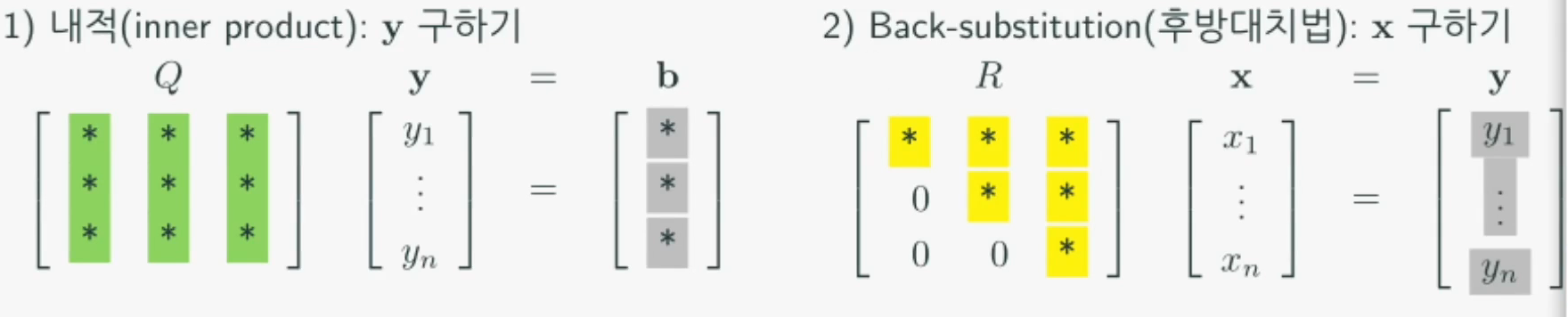
QR분해 (QR decomposition)의 의미

$QR$분해는 그람-슈미트 과정(Gram-Schmidt process)을 행렬로 코드화 한 것입니다

엄밀하게 말하자면,

• $Q$ : 행렬 $A$에서 정규직교성을 추출한 행렬
• $R$ : 행렬 $A$에서 정규직교성 추출 후 남은(residual) 상삼각행렬(upper traingular matrix)
  
  

여기서는 $QR$분해를 유도하는 수학적인 내용, 즉 그람-슈미트 과정(Gram-Schmidt process)은 다루지 않겠습니다. 다만, $QR$분해가 주어진 행렬에서 정규직교성을 추출하여 계산의 편의를 도모한다는 점을 기억하기 바랍니다.

• 그람-슈미트 과정(Gram-Schmidt process) 참고자료

  그람-슈미트 과정 - 위키백과, 우리 모두의 백과사전

  [선형대수] Gram-Schmidt Process, QR Decomposition

QR분해 (QR decomposition)의 활용

$QR$분해는 다음의 이유로 활용됩니다.

• 빠른 계산

  • 선형시스템 $A\bf x = b$의 해를 구할 때, 정규직교행렬(orthonormal matrix) $Q$를 이용한 계산 부분은 병렬처리로 빨리 계산할 수 있습니다.
  • 그러나, $R$을 이용한 계산 부분은 병렬처리 할 수 없습니다

• $\bf b$가 자주 업데이트 되는 경우

  • 선형시스템 $A\bf x = b$에서 행렬 $A$는 고정되어 있고 $\bf b$가 자주 변하는 문제가 종종 있습니다.

    이런 경우, 행렬 $A$를 미리 $QR$로 분해해 둔다면, $\bf b$가 업데이트 될 때마다 선형시스템의 해 $\bf x$를 실시간으로 구할 수 있습니다

$QR$ 분해 vs. $LU$ 분해

• $LU$ 분해의 경우, 선형시스템을 풀 때 병렬처리 할 수 없습니다
• $QR$ 분해의 경우, $Q$ 행렬이 꽉찬 구조를 가진 행렬이므로 메모리 사용량이 많습니다