집합(set)과 공간(space):
중등 교과과정부터 시작하기
집합(set)은 임의의 원소(element)를 수집하여 만든 모듬입니다
어떤 방식으로 모아도 되니, 다음과 같은 집합도 생각할 수 있습니다
연산에 닫혀 있는 집합(set)
집합이 연산에 닫혀있다 는 개념이 있습니다.
어떤 연산을 생각한 다음, 집합에서 임의의 원소를 뽑아 연산을 수행한 결과가 여전히 집합의 원소로 있다면, 해당 집합은 연산에 닫혀있다고 합니다
다음 집합은 덧셈 연산에 닫혀 있습니다. 곱셈 연산에도 닫혀 있습니다.
다음 집합은 덧셈 연산에 닫혀 있지 않습니다. 하지만 곱셈 연산에는 닫혀 있습니다.
공간(Space)
공간(space)은 다음의 두 연산에 닫혀있는 집합입니다
- 덧셈 연산에 닫혀있다
- 집합에서 임의의 두 원소 를 뽑아 더해도 그 결과 는 집합의 원소입니다
- 스칼라 곱 연산에 닫혀있다
- 집합에서 임의의 한 원소 를 뽑아 임의의 스칼라 배 한 결과 는 집합의 원소입니다
다음과 같이 -벡터의 집합은 모두 공간입니다
앞으로 모든 -벡터 집합 은 차원 벡터 공간(vector space)이라 부를 수 있습니다
열공간(Column Space)
행렬 의 열벡터들에 대한 가능한 모든 선형조합의 결과를 모아 집합으로 구성할 수 있을 것이다
이들 집합을 열공간(column space)이라 하고 다음과 같이 표기한다
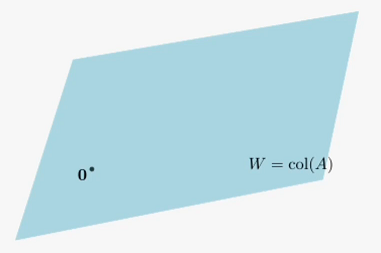
해가 있는 선형 시스템 (Consistent Linear System)
선형시스템 가 해를 가지면(consistent), 다음을 만족한다
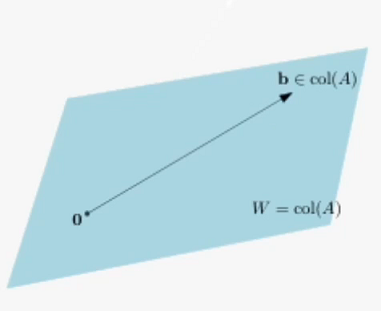
해가 없는 선형 시스템 (Inconsistent Linear System)
선형시스템 의 해가 없으면(inconsistent), 다음을 만족한다

최소제곱법(least squares method)
열공간(column space)으로 투영
선형시스템 에 대한 해가 없음에도 불구하고, 우리가 할 수 있는 최선이 무엇인가를 생각해보자
행렬 가 정의하는 열공간에서 우리의 목표 와 가장 가까운 지점은 를 열공간에 투영(projection)한 지점일 것이다.
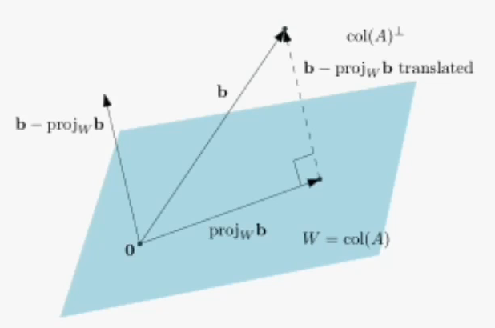
즉, 달성가능한 최선의 목표 를 생각할 수 있다.
를 구하지는 못하지만 내가 구할 수 있는 답 중 랑 가장 가까운 애까지는 찾아보겠다!!
최소제곱법(least squares method)?
최소제곱법은 선형시스템 에 대한 해 가 없음에도 불구하고, 할 수 있는 최선의 대안 를 내놓는 기법이다
최소제곱법은 원래의 선형시스템 가 아닌 다음의 선형시스템을 해결한다
이 방법은 목표 와 달성가능한 목표 의 차이를 나타내는 벡터 의 제곱길이를 최소화시키는 의미를 가지기 때문에 최소제곱법(least squares method)이라 불리운다
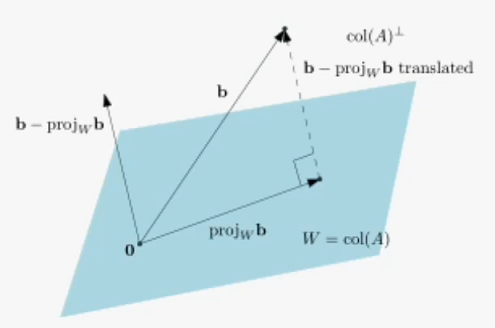
주어진 선형시스템의 양변에 전치행렬 를 곱하면 최소제곱법의 해를 구할 수 있다
최소제곱법으로 구한 해 는 원래의 선형시스템을 만족하는 해는 아니다
최소제곱법으로 구한 해 는 다음을 만족하는 근사해(approximate solution)이다.
최소제곱법의 응용: 선형회귀(Linear Regression)
2차원 공간에 개의 정점 이 그림과 같이 있을 때,
이를 잘 설명할 수 있는 직선 를 구하는 문제를 생각해보자.
이를 선형회귀(linear regression) 문제라 한다.
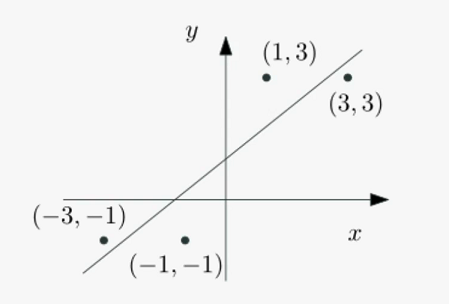
선형회귀 문제는 다음과 같이 최소제곱법으로 풀 수 있다
- 선형시스템 구성
- 직선이 각 정점을 모두 지나간다고 가정하고 선형시스템 구성
(단, 주어진 모든 정점을 지나가는 직선은 존재하지 않으므로 선형시스템의 해는 존재하지 않음)
- 직선이 각 정점을 모두 지나간다고 가정하고 선형시스템 구성
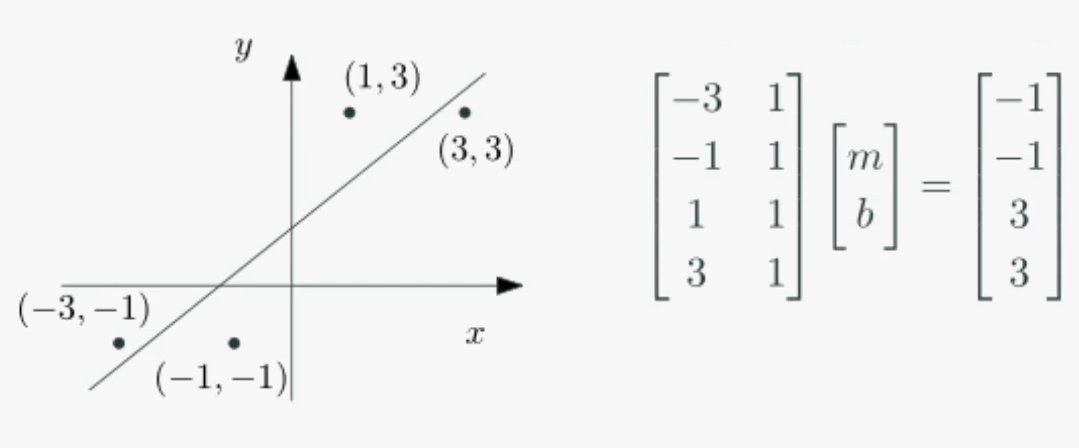
- 최소제곱법 적용
- 를 생각하고, 를 구한다
