통계학(Statistics)
데이터의 수집(collection), 구성(organization), 분석(analysis), 해석(interpretation), 표현(presentation)에 관한 학문
통계학은 두 가지로 구분될 수 있다:
-
기술통계학 (descriptive statistics)
- 수집된 데이터를 표현하고, 설명하는 통계학
-
추측통계학 (inferential statistics)
- 수집된 데이터를 분석하고 추측, 추론하는 통계학
기본 용어 정리
-
모집단(population)
-
어떤 질문이나 실험을 위해 관심의 대상이 되는 개체나 사건의 집합
-
ex. 전교생의 키, ...
그러나, 모집단 전체의 데이터로 뭔가를 파악하기에는 너무 양이 많고 어려움!
따라서, 모집단의 수치적인 특성(=모수)을 사용하여 데이터를 파악함
-
-
모수(parameter)
-
모집단의 수치적인 특성
-
ex. 키의 평균, 분산, 표준편차, ...
또한, 모집단 자체가 너무 큰 경우도 있음(예: 전국민의 키)
이 경우 데이터의 수집 자체에 비용과 시간이 너무 많이 들어감!
따라서, 우리가 알고싶은 모집단의 특성(=모수)를 추론하기 위하여 모집단의 일부(=표본)를 선택함!
-
-
표본(sample)
- 모집단에서 선택된 개체나 사건의 집합
- ex. 교내 30명 학생의 키, ...
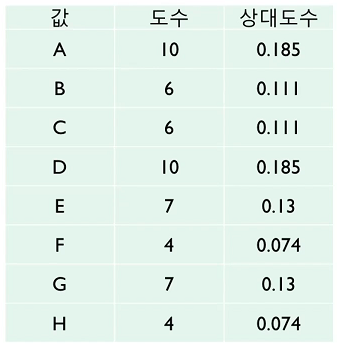
도수(Frequency)
-
정의
- 어떤 사건이 실험이나 관찰로부터 발생한 횟수
- ex. 키가 160~170cm인 학생이 몇 명인지, ...
-
표현방법
- 도수분포표(Frequency Distribution Table)
- 막대그래프(Bar graph)
- 질적 자료
- 수치적인 자료가 아니라 범주로 구분된 자료
- ex. (남, 여), (소설, 시, 에세이, ...)
- 히스토그램(Histogram)
- 양적 자료
- 수치적인 자료
- ex. 학생들의 키, ...
예
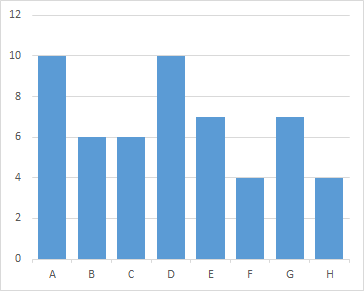
**<질적 데이터>** 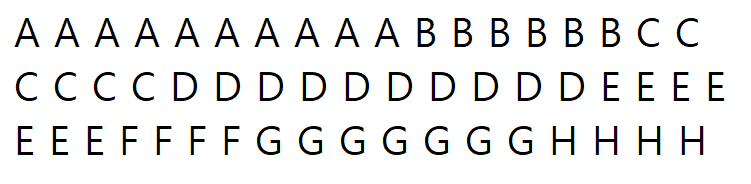각 데이터는 범주로 구성되어 있음
→ 도수분포표, 막대그래프
도수분포표
막대그래프
도수분포표에서도 데이터의 분포를 알 수 있지만, 막대그래프의 경우 한눈에 데이터의 분포(어느 알파벳이 많은지, 적은지)를 알 수 있는 장점이 있음
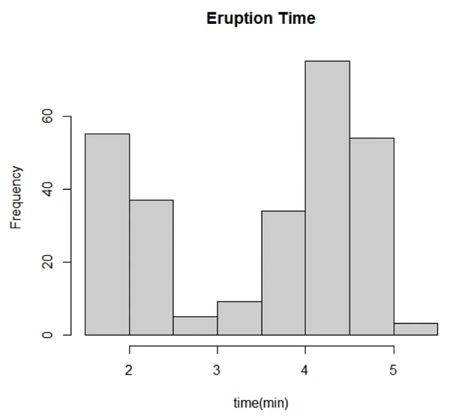
<양적 데이터>
각 데이터는 같은 값을 가질 확률이 매우 적음, 구간을 정해서 도수를 파악
→ 도수분포표, 히스토그램
히스토그램
막대그래프와 히스토그램은 유사하게 생겼지만,
막대그래프의 경우 막대의 순서가 상관없고 이산적(경계가 떨어져 있음)이지만
히스토그램의 경우 막대의 순서가 중요하고 연속적임(경계가 붙어있음)
줄기 - 잎 그림(Stem and Leaf Diagram)
양적 자료를 줄기와 잎으로 구분
자료들을 정렬한 다음 숫자들을 잘라(예: 앞에 두개 숫자) 범주를 만든다(=줄기)
나머지 부분들은 나열한다(=잎)
데이터의 분포를 시각적으로 알 수 있고, 어떤 값들이 있는지 파악할 수 있다

16.0 16.7 17.0 17.3 17.5 17.5 ... 17.8
18.0 18.0 18.0 18.0 18.2 18.2 ...
... 51.0상대도수(Relative Frequency)
도수를 전체 원소의 수로 나눈 것
Python 모듈 설치
통계에 필요한 파이썬 모듈
pip install numpy scipy matplotlib pandas sympy nose평균(Mean)

- 모평균
- 모집단 전체 자료일 경우
- 표본 평균
- 모집단에서 추출한 표본일 경우
중앙값 (Median)
평균의 경우 극단 값(outlier)의 영향을 많이 받음!!

중앙값(Median)이란?
주어진 자료를 높은 쪽 절반과 낮은 쪽 절반으로 나누는 값을 의미
자료를 순서대로 나열했을 때 가운데 있는 값
자료의 수 = 일 때,
-
이 홀수 : 번째 자료값
-
이 짝수 : 번째와 번째 자료값의 평균

분산(Variance)
편차의 제곱의 합을 자료의 수로 나눈 값
-
편차 : 값과 평균의 차이
-
값들이 평균을 기준으로 얼마나 퍼져 있는지? (산포 정도)를 알고 싶을 때 사용
-
모분산
-
자료가 모집단일 경우
-
-
표본 분산
-
자료가 표본일 경우
-
이 때, 자료의 개수 이 아닌 로 나누는 것에 주의!
-

b의 분산이 매우 큰 이유는 극단값 때문! (제곱까지 했기 때문에 더 심함)
표준편차(Standard Deviation)
분산의 양의 제곱근
-
모표준편차(population standard deviation)
-
표본표준편차(sample standard deviation)
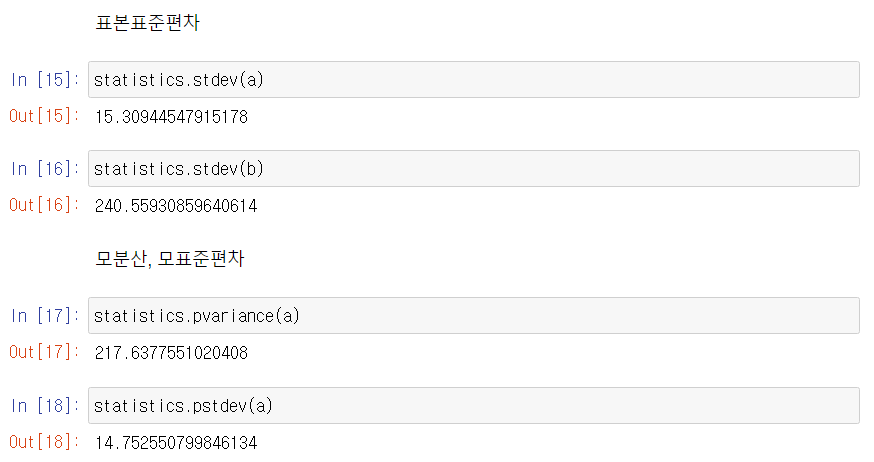
numpy 모듈로도 계산 가능
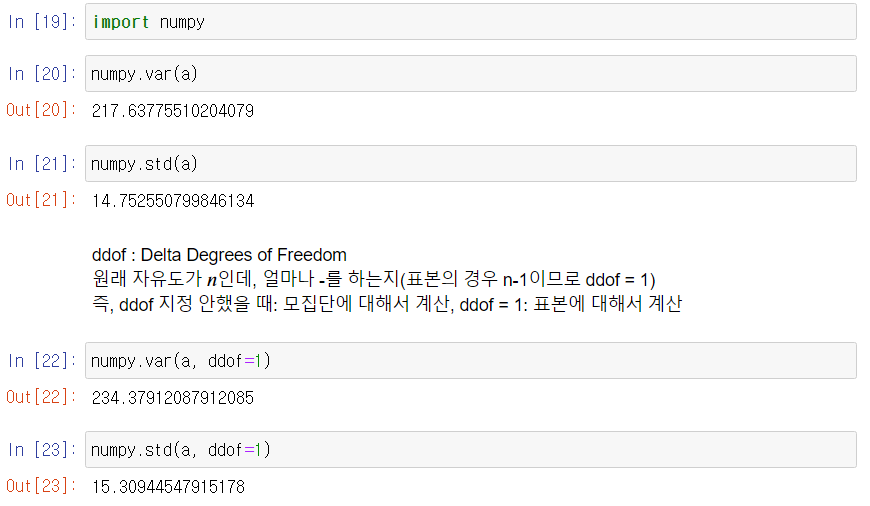
범위(Range)
자료를 정렬하였을 때 가장 큰 값과 가장 작은 값의 차이

범위로 이상값(=극단값)을 발견하기는 힘듦
자료의 범주별로 값의 범위가 크게 차이날 때(예: 키와 눈동자 크기) 각 자료의 값을 범위로 나눠 스케일을 맞춤!
사분위수(Quartile)
전체 자료를 정렬했을 때 위치에 있는 숫자
- Q1 : 제 1사분위수
- 지점 ? → 중앙값(Median)
- Q3 : 제 3사분위수
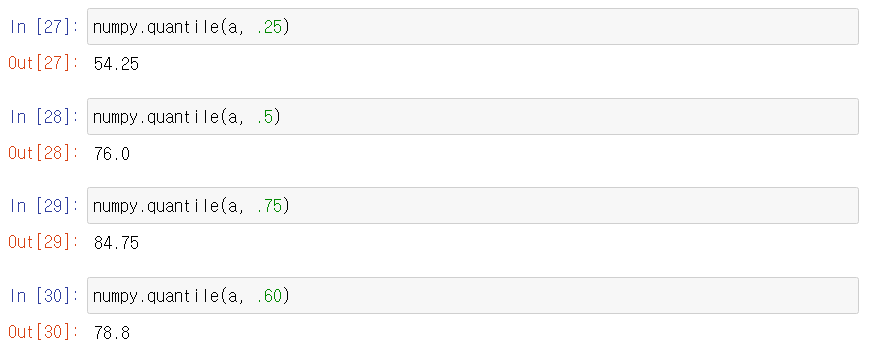
quantile은 백분위수를 의미한다.
numpy.quantile() 함수는 두 번째 인자로 꼭 사분위수만 들어가야 하는 것은 아님!
quantile의 특별한 경우를 quartile, 사분위수라고 말함
사분위범위 (IQR, interquartile range)
Q3 - Q1을 의미

z-score
어떤 값이 평균으로부터 몇 표준편차 떨어져 있는지를 의미하는 값
수집된 데이터의 종류에 따라 값의 절대차가 많이 차이나기 때문에 절대차는 의미가 없음
- 모집단의 경우
- 표본의 경우

각각의 값들에 대해 z-score를 구할 수 있음