Fine Grained Visual Classification - (1)

Learning Class Unique Features in Fine-Grained Visual Classification

Objectives

• 본 논문은 Fine-Grained Visual Claissification에서 높은 inter-clsdd similarity를 갖는 다양한 category를 구분짓는 결정적인 detailed feature을 학습 하기 위한 새로운 loss function을 제시한다.
• 각 category의 feature들의 uniqueness를 CNN이 학습할 수 있도록 정보 이론의 관점에서 접근한다.

1. MiniMax Loss based on a game theoretic framework
2. Feature Redundancy Loss
   • MiniMax Loss를 통해서 redundant feature을 배울 수 있기 때문에 각각의 설정된 feature map사이의 normalized inner product 또한 줄이도록 정규화 항을 사용한다.
   • 즉, 다른 category임에도 동일한 channel이 activate되어서 각 category마다 동일한 spatial domain에 집중하게 되는 상황이 있을 수 있기 때문에 이를 막기 위함이다.

Related Works and Propopsed Method

• FGVC와 관련된 연구들에 대해 알아보자.

1. Attention Mechanism and part localization

   → 모델이 inter-class variation을 포함하는 feature이나 region에 집중할 수 있도록 모델을 학습한다.

   • One-Squeeze Multi-Excitation을 사용해서 다수의 attention map이 discriminative part를 효과적으로 얻을 수 있도록 한다.
   • Sparse attention for feature sampling으로 context information을 잃지 않으면서 visual detail을 잡으려 했다.

2. High order statistics

   → max-pooling이나 average-pooling같은 first-order statistics로는 다양한 카테고리간의 feature의 diversity를 잡기가 어려워서 bilinear pooling, 또는 두개의 CNN feature extractor branch의 output에 외적을 해서 local pairwise feature interaction을 계산하는 방법을 사용하였다.

3. Regularization based methods

   → Overfitting을 방지하기 위한 노력의 일환이다.

   • 흔히 아는 wight의 Frobenuius norm을 minimize해서 weight가 너무 커지는 것을 방지하는 방법이 있다.
   • 또는 Random한 pair의 output probability distribution간의 L2 distance를 최소화하여서 모델에 혼선을 주어 과적합을 방지한다.

   ⇒ 본 논문 또한 output distribution의 regularization에 기반을 하기 때문에 유사한 task에 대한 lightweight solution이 될 수 있다.

MI (Mutual Information)

→ 정보이론에서 정보량을 계산하기 위해서 사용된다.

MI는 joint distribution P(X,Y)가 P(X)P(Y)와 얼마나 비슷한지를 측정하는 척도이다.

만약에 위의 식에서 X와 Y가 독립이라고 한다면 P(X, Y) == P(X)P(Y)이기 때문에 log1=0이 되어서 I(X;Y)도 0이 된다. 따라서 두 변수가 독립에 가까울수록 MI도 작아지는 상황이다.

이를 conditional entropy로 다시 표현하면 아래와 같이 나타낼 수 있다.

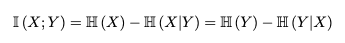
즉, Mutual Information은 X에 대한 불확실성에서 Y를 알고 난 후에 X에 대한 불확실성 (=엔트로피)를 삔 값이다. 결국 Y의 정보를 알게 됨으로서 X에 대한 엔트로피의 감소량이라고도 해석 할 수 있다.

⇒ 위의 식에서 $H(X|Y) = H(X,Y)-H(Y)$이다.

또, 엔트로피에서 중요하게 알고 가야 하는 성질은 균등(Uniform) probability distribution을 갖는 경우에 불확실성, 즉 엔트로피가 제일 작은 값을 갖는다는 것이다. 같은 맥락에서 볼 때 하나의 클래스가 무조건 결정적이다 라고 할 때 1의 확률을 갖게 되기 때문에 $\sum p(x_{i})log_{2}(p(x_{i}))$의 값이 0으로 최소의 엔트로피의 값을 갖게 된다.

• 실제로 정보 이론의 개념은 GAN 모델을 학습 할 때에도 사용이 된다. GAN은 latent vector Z를 입력으로 받아서 최대한 원래 이미지와 같은 데이터를 만들도록 한다. 여기에 adversarial loss까지 추가해서 discriminator이 generator에 의해서 생성되는 데이터의 진위 여부를 구분하게 한다.
• 하지만 generator과 discriminator 둘 중 하나가 너무 학습이 잘 돼서 다른 하나의 학습이 잘 진행되지 않는 mode-collapse라는 한계가 존재하기는 한다.
• 기본적인 GAN모델에서는 discriminator은 Cross Entropy Loss로, generator은 L2 loss를 많이 사용하기는 한다. 또, discriminator이 generator에 의해 만들어진 데이터에 대한 진위 여부의 점수가 1에 가깝게 (REAL이라고 예측하도록) 진짜와 같이 생성하도록 하는 것이 generator의 objective function이다.

Proposed Method

→ 저자들이 이루고자 했던 것은 non-target class의 information을 포함하지 않는 feature을 extract하는 것이었다. 이는 extracted feature과 non-target output distribution 간의 MI를 최소화 하기 위해서 구현이 될것이라 판단 하였다.

→ 그래서 아래의 식을 최소화 하는 것을 목표로 둔다.

위의 식에서 $\theta$는 모델의 파라미터이고, $\phi(X)$는 입력 X에 대한 feature map이며, 정답이 t인 것이다. 한편, $\hat{Y}_{Ct}$는 정답 t가 아닌 class에 대한 예측 확률 분포이다. 이 둘의 MI를 최소화 하기 위해서는 마지막 식의 첫번째 항이 모든 probability가 동일한 균등 분포일때 최대임을 사용해서 X^t에 대한 non-target class의 확률도 모두 균등한 경우에 최솟값인 0이 될 수 있음을 보인다.

→ 결과적으로 학습의 목표는 정답 class $t$가 아닌 class에 대한 probability estimation의 값을 모두 균등하게 예측하도록 하는 것이다.

→ 이렇게 학습을 하기 위해서는 게임 이론에서 영감을 얻어서 method를 설계하였는데, 모델이 예측한 각 class에 대한 probability 중에서 정답이 아닌 class에서 제일 적은 probability로 예측한 class를 일부러 모델이 정답에 대해 예측한 probabiliry를 1에서 뺀 값으로 adversary target을 지정해 준다.

→ 이 방법을 사용하면 모델이 수렴함에 따라서 정답 class가 아닌 나머지 class는 모두 균등하게 예측할 수 있을 것이다.

→ 그리고 여기서 멈추지 않고 feature redundancy loss를 추가하는데, 이는 feature redundancy 를 줄이기 위한 목적으로 적용이 된다.

→ 그래서 model이 class uniqueness는 유지하면서 더 diverse feature을 고를 수 있도록 feature map중에서 top K activation score을 갖는 feature mapd르 선택해서 normalized inner product를 계산하여 이를 정규화 항으로서 앞선 MM Loss에 더해주어 LOSS FUNCTION으로 사용한다.