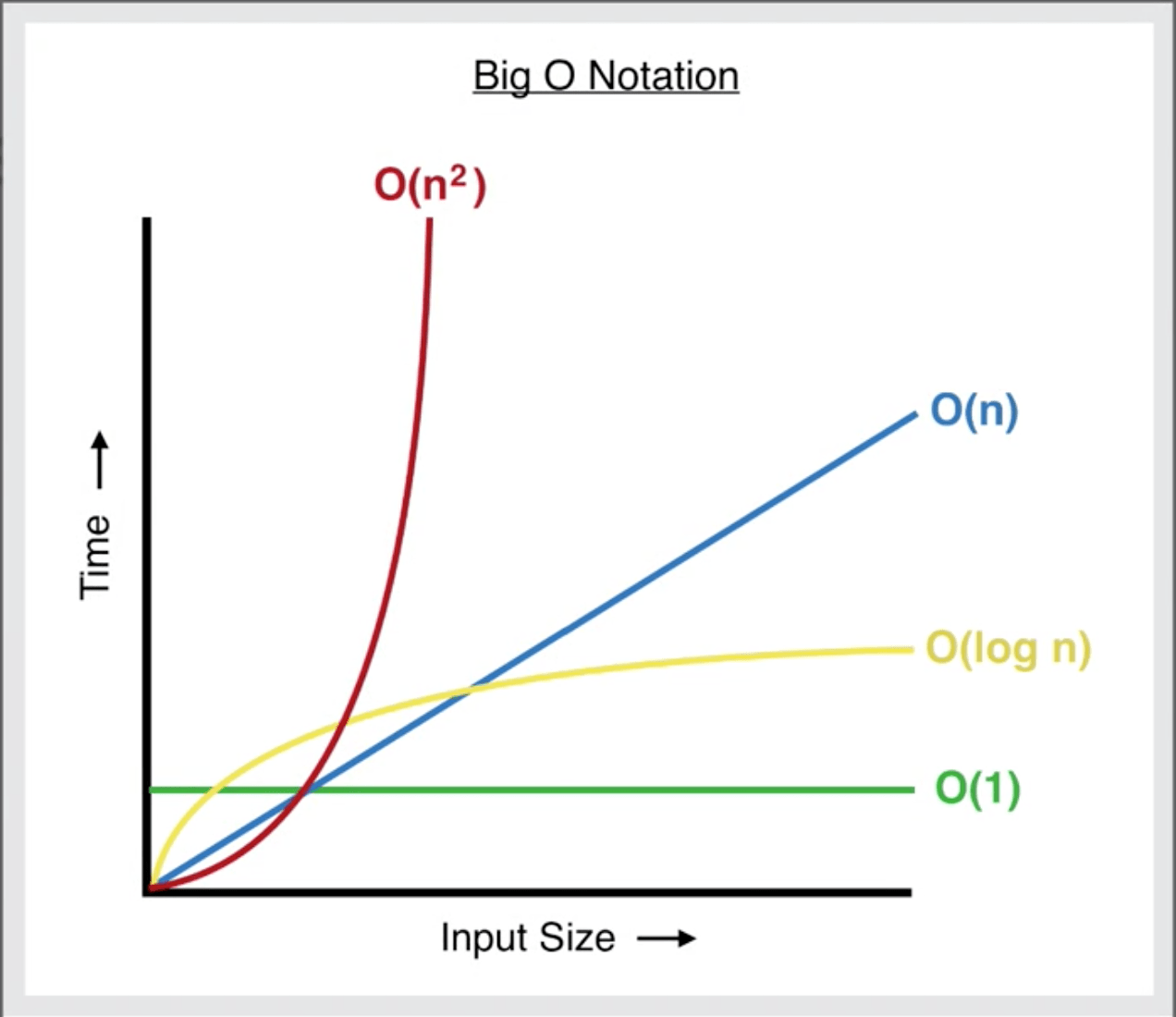
오늘 이야기할 주제는 알고리즘을 하면 빼놓을 수 없는 주제 Big O이다.
알고리즘을 공부하다보면 한번 쯤 O(log n)으로 구현하라 O(n)으로 구현하라는 이야기를 본 적이 있을 것이다.
학창시절에 수학책에서 log를 본 경험이 있으니, 대충 이해는 하고 있었지만, 오늘 궁금증을 풀기위해 검색해 보았다.
주 내용은 노마드 코더 Big O를 참고했다.
O(1)
가장 작은 복잡도를 가진 알고리즘이다.
function print(arr) {
console.log(arr[0]);
}만약 arr의 length가 얼마이건 간에 한 번의 step으로 함수가 끝난다.
그럼
function print(arr) {
console.log(arr[0]);
console.log(arr[1]);
}이 함수는 2번의 step으로 이루어져 있으니 O(2)라고 할까?
정답은 아니다 이 함수도 동일하게 O(1)이다.
Big O는 전체적인 원리를 표현하는 방식이지 작은 디테일까지 표현하지는 않는다.
O(n)
O(n)을 가장 쉽게 이해하는 것을 우리에게 익숙한 for문을 보면 된다.
let arr1 = [0, 1, 2, 3, 4];
let arr2 = [0, 1, 2, 3, 4, 5, 6, 7, 8];arr1 이라는 배열에서 for문으로 element 4를 찾으려면 arr1 배열의 길이와 동일한 5번을 searching해야 한다.
그리고 arr2 라는 배열에서 for문으로 element 8을 찾으려면 arr2 배열의 길이와 동일한 9번을 searching해야 한다.
그러면 arr3이라는 배열이 있고 arr3.length가 n일때, 마지막 index를 찾으려고 하면 n번 만큼 searching해야 할 것이다.
이런 알고리즘을 O(n)이라고 표현한다.
O(n2)
보통 복잡도가 O(n2) 별로 좋지않은 알고리즘이다.
가장 좋은 예시는 버블정렬이다.
버블정렬이란?
버블정렬에 대한 설명을 하면 너무 길어져서 위의 링크로 대체하겠다.
O(log n)
보통 알고리즘에서 복잡도를 O(log n)으로 하라고 하면, Binaray Search Tree(이진 탐색 트리)를 구현해야 하나.
이진 탐색 트리는 쉽게 설명하면 sorted되어있는 (오름차순 or 내림차순) 자료를 반씩 쪼개가면서 탐색하는 것이다.
let sortedArr1 = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];위의 정렬된 배열에서 5을 찾는다고 생각해 보자.
그럼 처음 반으로 쪼개서 4와 5을 비교한다. 6은 4보다 크니까 배열에서 4보다 작은 요소들은 더 이상 살펴 볼 필요가 없다.
그래서 4보다 큰 요소를 반으로 쪼개서 7을 검색한다. 7은 5보다 크니까, 7이상의 요소들은 더이상 살펴볼 필요가 없다.
마지막으로 5와 6이 남았을때 5을 살펴보고 찾던 숫자와 일치함으로 탐색을 그만둔다.
let sortedArr2 = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]만약 배열의 요소가 두 배가 되어도 처음 반으로 쪼깨면 sortedArr1의 요소의 개수와 동일해져서 step이 한번만 증가할 뿐이다.
그래서 이진 탐색 트리의 복잡도를 O(log n)이라고 표현하는 것이다.