
동적 계획법(DP, Dynamic Programming)
개념
- 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용한다.
- 주어진 문제를 여러 개의 소문제로 분할하여 각 소문제의 해결안을 바탕으로 주어진 문제를 해결, 이때 각 소문제는 다시 또 여러 개의 소문제로 분할 가능하다. 각 소문제는 원래 주어진 문제와 동일한 문제이지만 입력의 크기가 작다.
일반적인 재귀 방식(Native Recursion)과 DP는 매우 유사하다.
큰 차이점으로는 일반적인 재귀를 단순히 사용 시 동일한 작은 문제들이 여러 번 반복되어 비효율적인 계산이 될 수 있다는 것이다. 출처
ex) 피보나치 수열
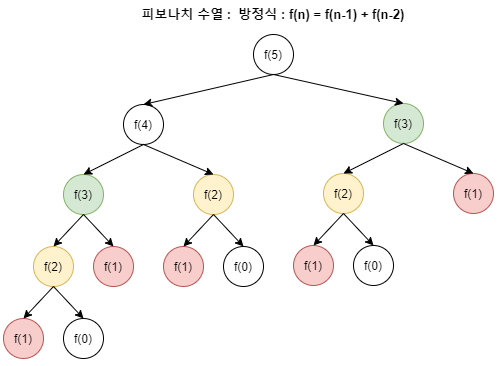
: 소문제의 결과가 상위 문제의 결과를 찾는 데 사용됨으로 각각의 소문제는 중복된다. 같은 소문제를 여러 번 반복해 계산하다 보니 자원 낭비가 심하고, 시간이 더 걸린다.
=> 그래서 동적 계획법은 소문제의 해를 따로 저장해놓고 이를 더 큰 문제를 푸는데 이용 (한 번 푼 문제는 다시 풀지 않고 저장 해둔 값을 사용함으로써 자원 및 시간을 절약함)
- 시간 복잡도 개선 O(n^2) => O(f(n)) (다항식의 경우 해당)
DP 사용 조건 (어떤 문제에 적용해야 할까?)
1. 겹치는 부분 문제 (Overlapping Subproblems)
- 문제를 나누고, 그 문제의 결과 값을 재활용해서 전체 답을 구한다. 그래서 동일한 작은 문제들이 반복하여 나타나는 경우에 사용이 가능하다.
- 부분 문제가 반복적으로 나타나지 않는다면 재사용이 불가능하니 부분 문제가 중복되지 않는 경우에는 사용할 수 없다.
2. 최적 부분 구조 (Optimal Substructure)
특정한 경우에 사용하는 알고리즘이 아니라 하나의 방법론이므로 다양한 문제해결에 쓰일 수 있다.
1) DP로 풀 수 있는 문제인지 확인
: 작은 문제들로 이루어진 하나의 함수로 표현될 수 있는지 판단 ( 보통 특정 데이터 내 최대화/최소화 계산을 하거나 특정 조건 내 데이터를 세야 한다거나 확률 등의 계산의 경우 DP로 풀 수 있는 경우가 많다)
2) 문제의 변수 파악
: ex) 피보나치 수열에서 n번째 숫자를 구하는 것이므로 n이 변수다.
3) 변수 간 관계식 만들기 (점화식)
: ex) 피보나치 수열에서의 점화식 f(n) = f(n-1) + f(n-2)
4) 메모하기(memoization or tabulation)
: 변수의 값에 따른 결과를 저장한다. 결과를 저장할 배열 등을 미리 만들고 그 결과를 나올 때마다 배열 내에 저장하고 그 저장된 값을 재사용하는 방식으로 문제를 해결
5) 기저 상태 파악하기
: 가장 작은 문제의 상태를 알아야한다. ex) 피보나치 수열에서는 f(0)=0, f(1)=1
6) 구현하기
: 1. Bottom-Up (Tabulation 방식) - 반복문 사용
: 2. Top-Down (Memoization 방식) - 재귀 사용
=> 최적성의 원리를 만족하는가?
최적성의 원리란 주어진 문제의 부분해가 전체 문제의 해를 구하는데 사용되는지를 의미한다.
코드
ex) 피보나치 수열
Bottom-Up (Tabulation 방식/상향식) - 반복문 사용
: 아래에서부터 계산을 수행하고 누적시켜서 전체 큰 문제를 해결하는 방식
: 메모를 위해서 dp라는 배열을 만들었고 이것이 1차원이라 가정했을 때, dp[0]가 기저 상태이고 dp[n]을 목표 상태라고 하자.
: Bottom-up은 dp[0]부터 시작하여 반복문을 통해 점화식으로 결과를 내서 dp[n]까지 그 값을 전이시켜 재활용하는 방식이다.
# DP
# 타뷸레이션 (상향식)
def fib(n):
dp = [0]*(n+1)
dp[0] = 1
dp[1] = 1
# 작은 값(소문제)부터 직접 계산하며 진행
for i in range(2,n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
fib(10)
[출처](https://lsh424.tistory.com/76)Top-Down (Memoization 방식/하향식) - 재귀 사용
: dp[0]의 기저 상태에서 출발하는 대신 dp[n]의 값을 찾기 위해 위에서 부터 바로 호출을 시작하여 dp[0]의 상태까지 내려간 다음 해당 결과 값을 재귀를 통해 전이시켜 재활용하는 방식이다.
# DP
# memoization (하향식)
dp = [0]*100 # 소문제 결과를 저장할 리스트
dp[0] = 1
dp[1] = 1
def fib(n):
# 만약 계산한 적이 없다면 재귀로 계산
if dp[n] == 0:
dp[n] = fib(n-1) + fib(n-2)
# 있다면 그대로 반환
return dp[n]
fib(10)
[출처](https://lsh424.tistory.com/76)계단은 1칸이나 2칸씩 오를 수 있다. 꼭대기까지 계단을 오르는 방법의 총 경우의 수는?
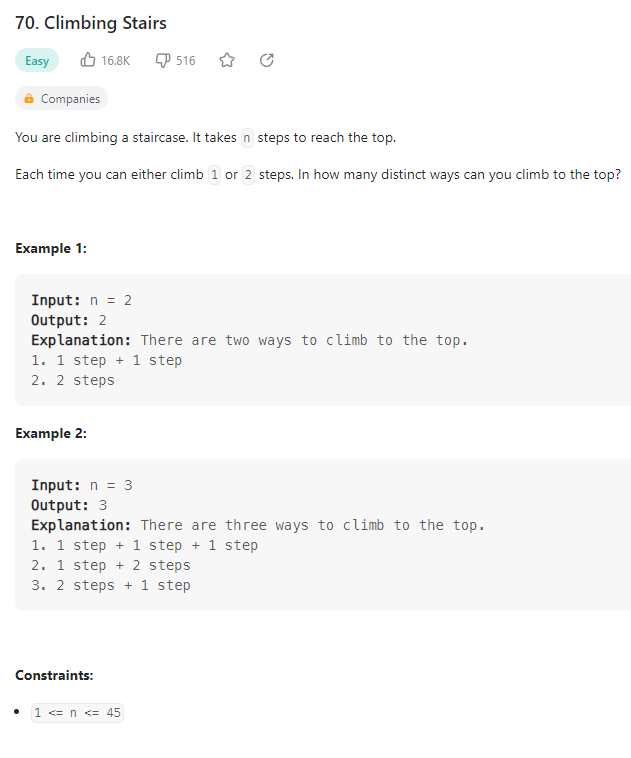
1) DP로 풀 수 있는 문제인지 확인 => Yes
2) 문제의 변수 파악 => n층에서의 오르는 방법의 수를 구하는 것
3) 변수 간 관계식 만들기 (점화식) => n>2일 때, C(n) > C(n-1) + C(n-2)
- 1 계단 : 1
- 2 계단 : 1+1 / 2
- 3 계단 : 1+1+1 / 1+2 / 2+1 (2계단을 오른 후 1계단을 오르거나 1계단을 오르고 2계단을 오르는 경우를 더해주면 됨)
- 4 계단 : 1+1+1+1 / 2+2 / 2+1+1 / 1+1+2 / 1+2+1
...
이전에 구했던 부분해를 전체 문제의 해를 구하는데 사용함. => 최적성의 원리 만족
4) 메모하기(memoization or tabulation) => Yes
5) 기저 상태 파악하기 => c[0] = 1, c[1]=2
6) 구현하기 =>
def climbStairs(n: int) -> int:
c = [0]*(n+1)
c[0] = 1
c[1] = 2
if n < 3:
return c[n-1]
for i in range(2,n):
c[i] = c[i-1] + c[i-2]
return c[n-1]
climbStairs(5)
[출처](https://lsh424.tistory.com/76)