BPTT(backpropagation through time)

RNN과 DMLP의 유사성

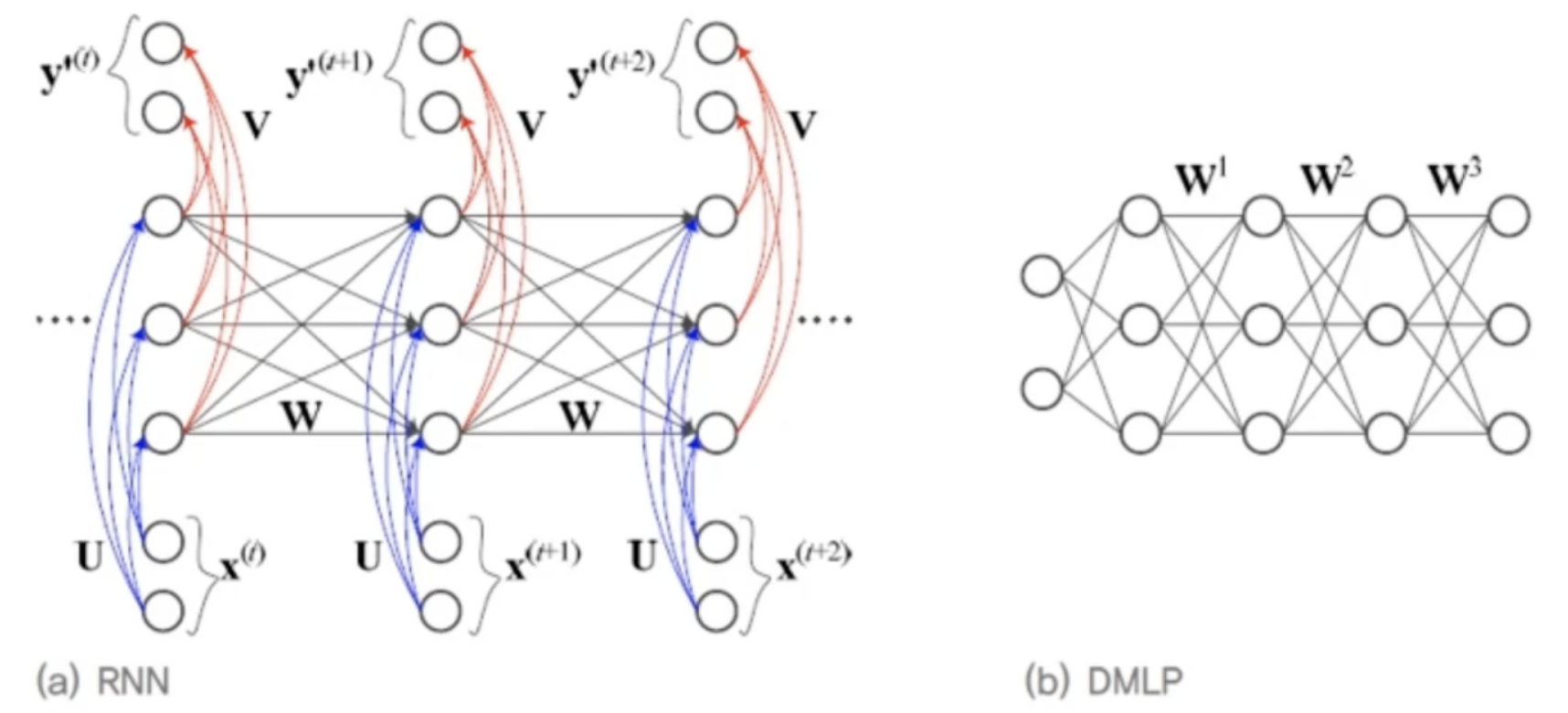
• 둘 다 입력층, 은닉층, 출력층을 가짐
• 왼쪽 그림은 노드를 DMLP와 비교하기 쉽게하기 위해 수직으로 배치한것!

RNN과 DMLP의 차별성

• RNN은 샘플마다 은닉층의 수가 다름
• DMLP는 왼쪽에 입력, 오른쪽에 출력이 있지만, RNN은 매 순간 입력과 출력이 있음
• RNN은 가중치를 공유함
• DMLP의 가중치는 각 은닉층별 벡터 W^1, W^2, W^3
• RNN은 행렬 W로 표기

목적함수 선정

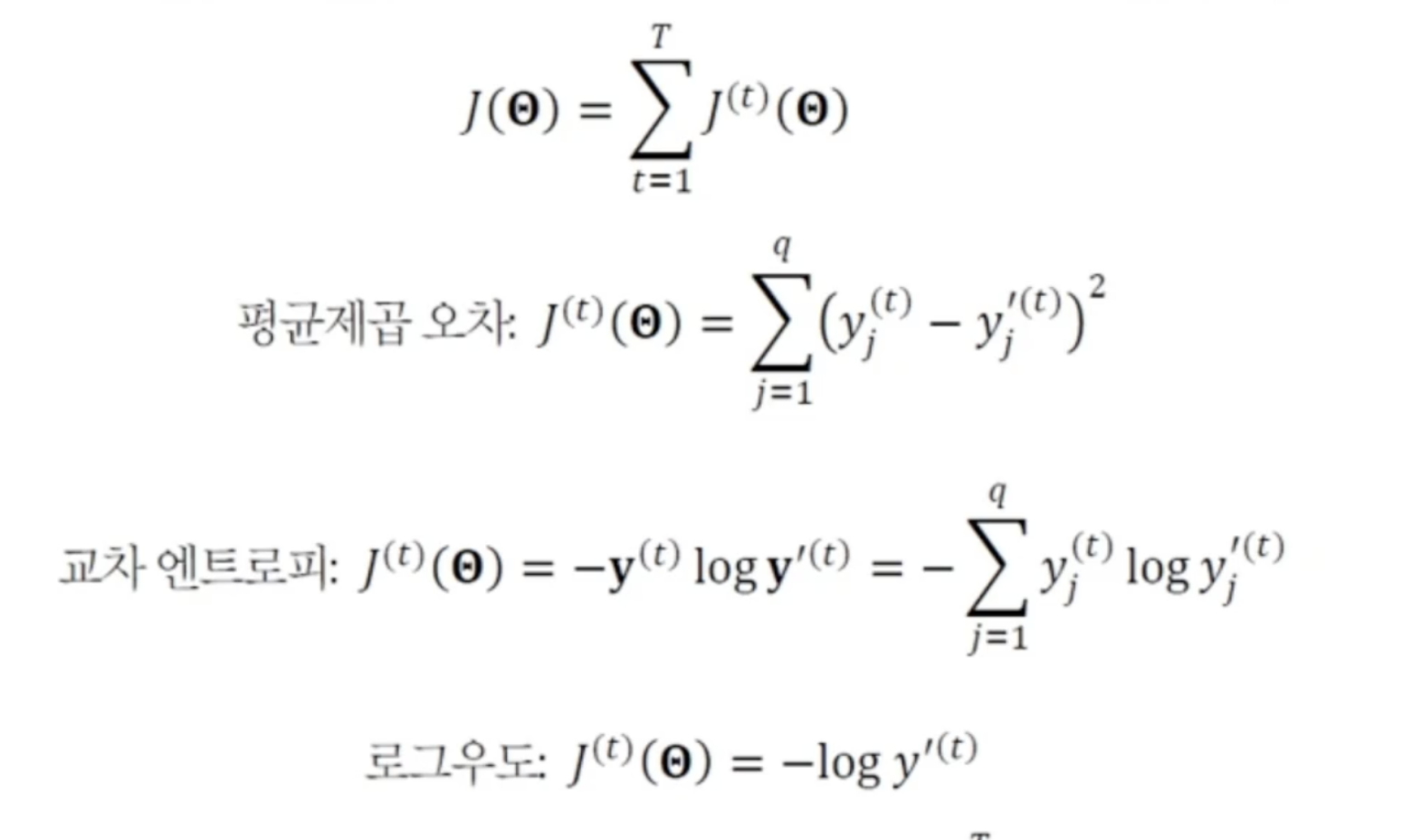
• 평균제곱 오차, 교차 엔트로피, 로그우도 중에 선택해서 사용

경사도 계산

V값으로 미분

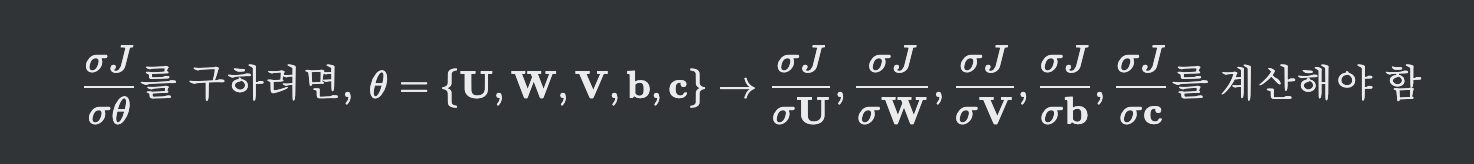
• 각 매개변수 별 경사도를 구해야함

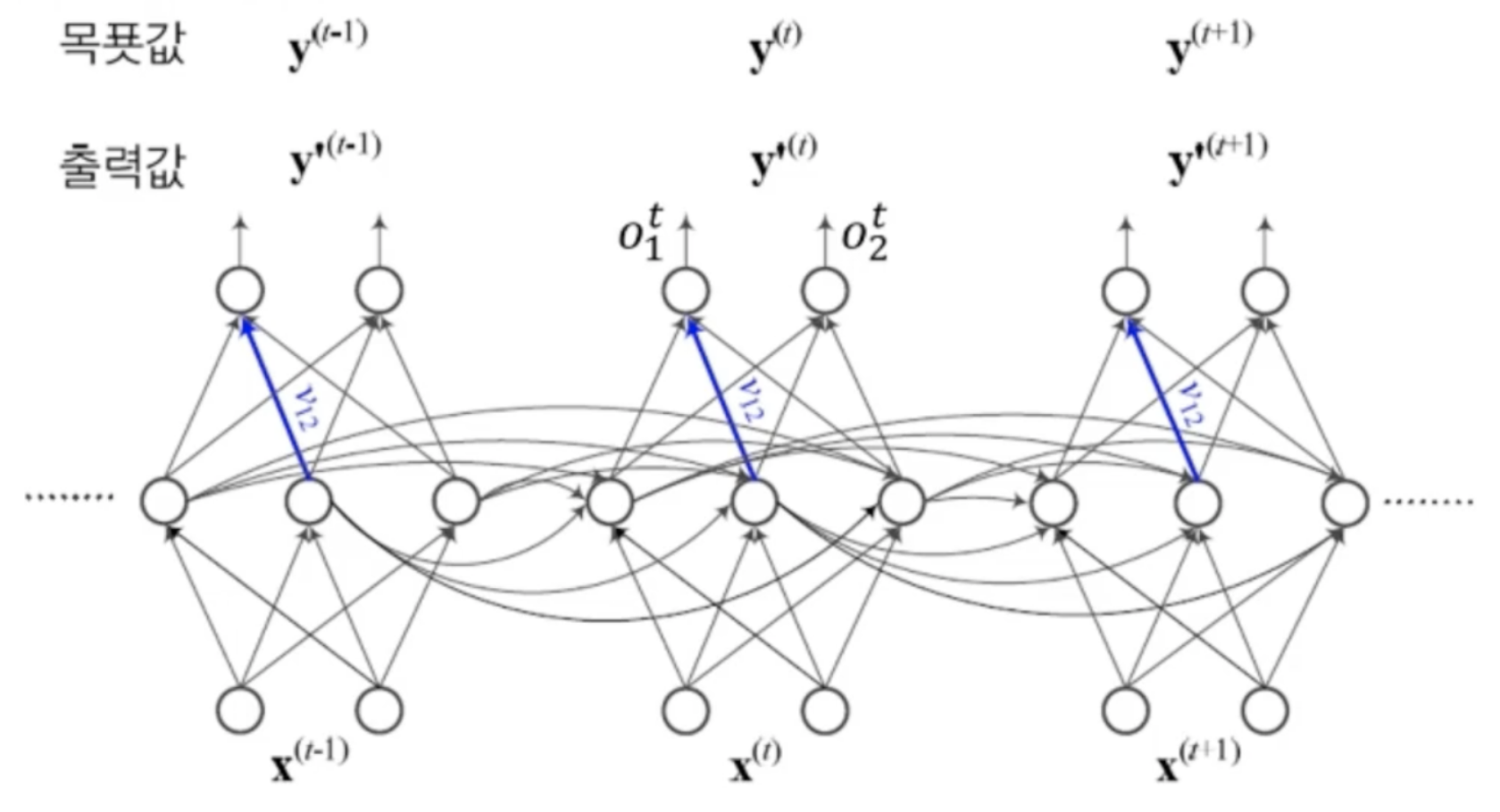
• 그 중에서 V값에 대한 경사도 계산이 제일 간단함

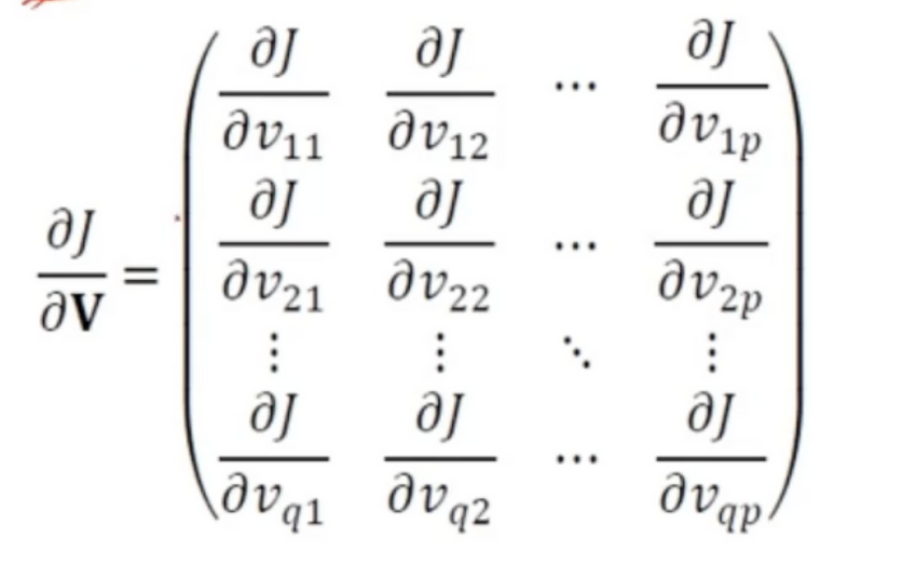
• J에 대한 V의 편미분값은 행렬 형태를 띄고 있음

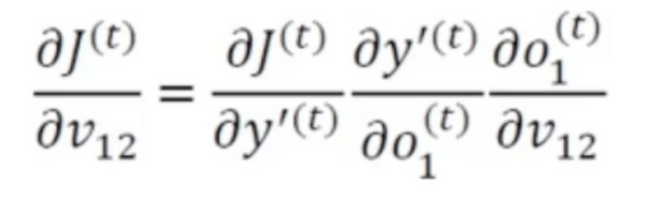
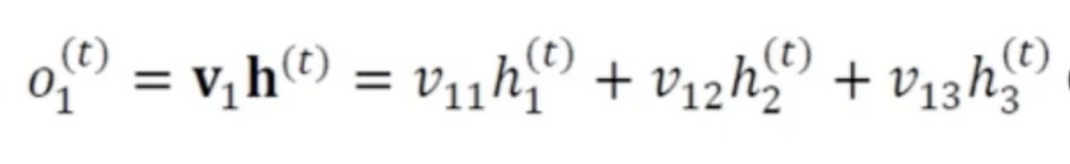
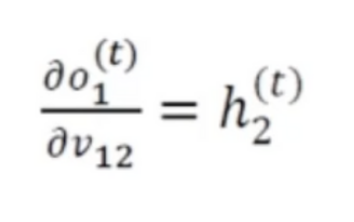
• 로그우도를 사용하기로 하고 v_12로 미분하기 위해 연쇄법칙을 적용
• o1은 3가지의 은닉층*가중치 결과를 종합한 결과므로 v_12항만 남기고 사라지는 편미분

• 로그우도를 사용하기에 y = (1,0), y = (0,1)인 경우로 나눠서 생각해야하는데
• 위 식은 (1,0)인 상황
• 로그 우도를 사용해서 계산해보면 -1+y 결과가 나옴

• 두 가지 유도를 합쳐보면 위처럼 식이 정리가 됨

• v_12를 v_ji로 일반화하고, 2부류를 q개 부류로 일반화 한 위 식

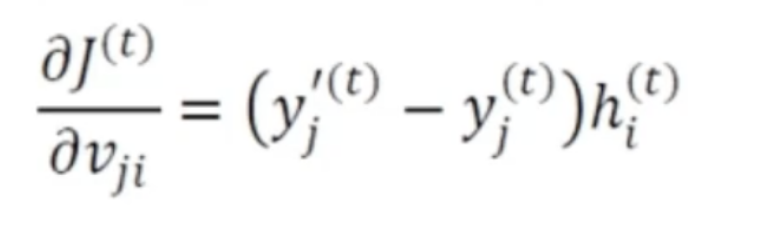
• 좀 더 간결한 표현

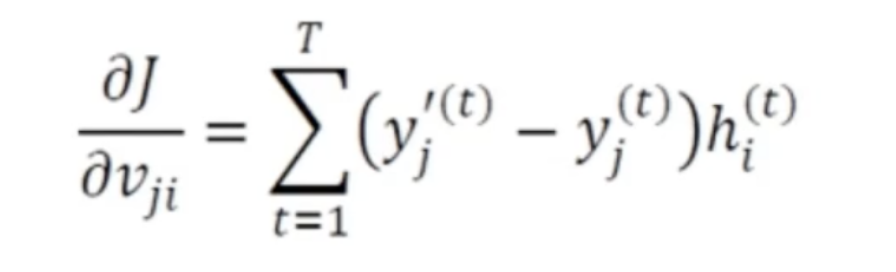
• 모든 예측값에 대한 식으로 정리

• 이 식을 v 행렬 전체를 위한 식으로 확장하고 목적함수에 대한U, W, b, c 미분까지 유도하면 BPTT가 완성!
  

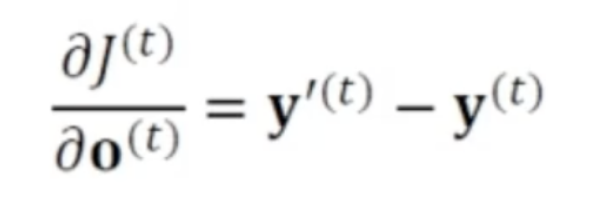
• 매개변수에 대한 작업에 필요한 식을 벡터 형태로 일반화

은닉층에서의 미분

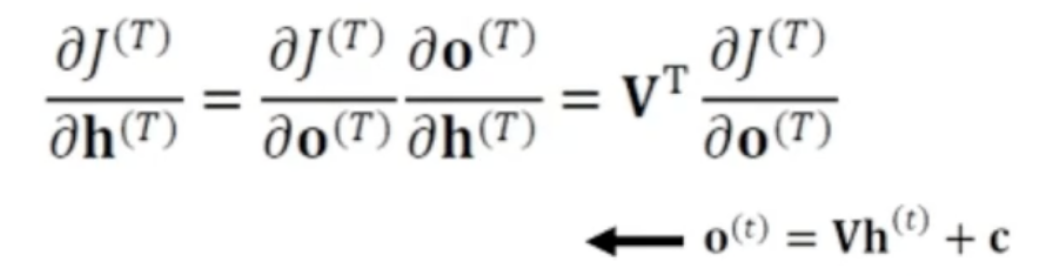
• 은닉층값의 미분은 이후 은닉층과 출력층에 영향을 주므로 V로 미분하는 것보다 복잡함
• 위 식은 추가 은닉층이 없는 마지막 순간에 대한 미분식

• T-1 순간의 경사도를 유도한 식

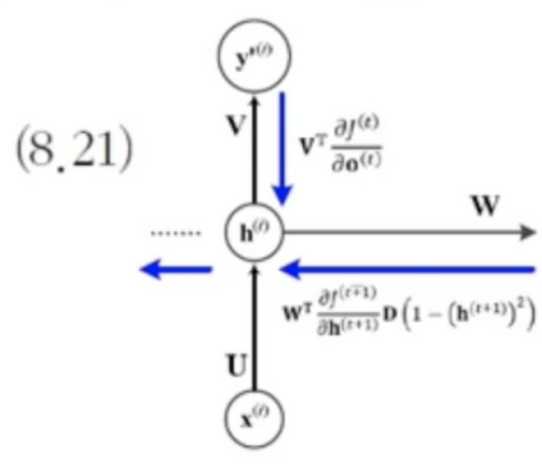
• t 순간으로 일반화 하면, 경사도를 역전파하는 위 순환식을 얻음

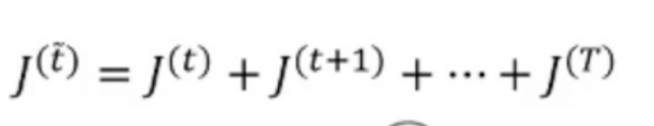
-t를 포함해 이후 목적함수의 값을 모두 더한 값 정의

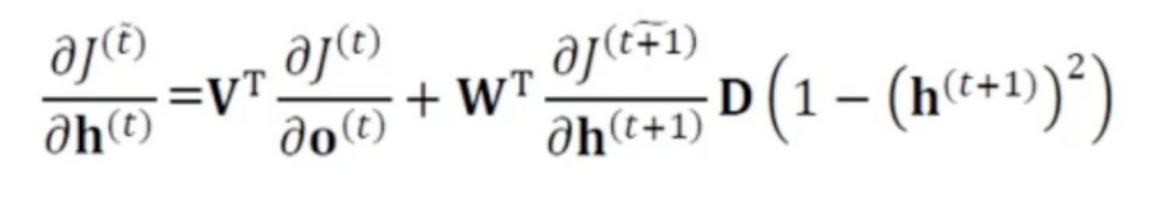
• 목적함수 값을 다 더한값에서 t 은닉층값에 대한 미분식은 위처럼 정리

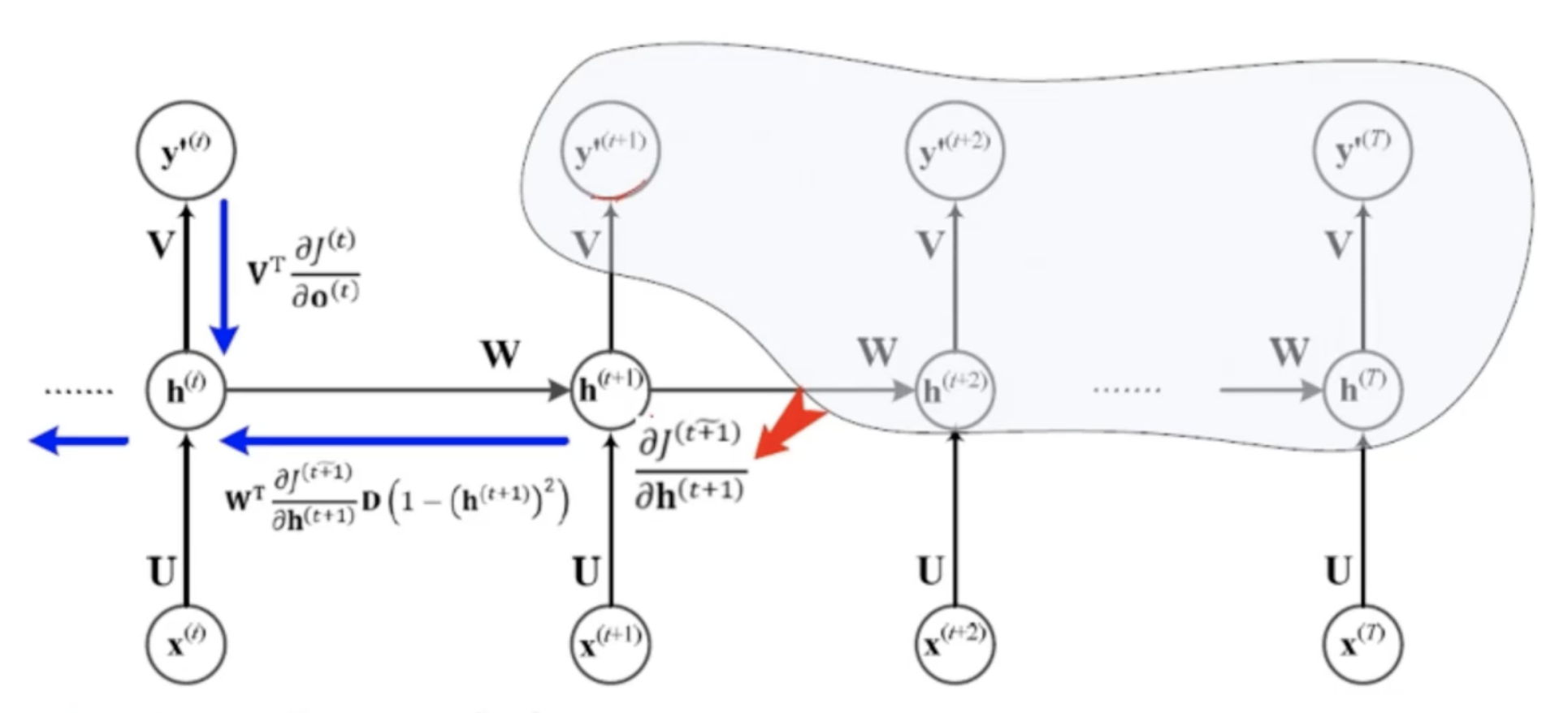
• RNN 가중치 갱신은 직접적인 결과로부터 오는 미분값+넘겨준 h에 의한 W로 발생한 결과값으로부터 오는 미분값도 고려해야함
• 시간 순서로 영향을 받음

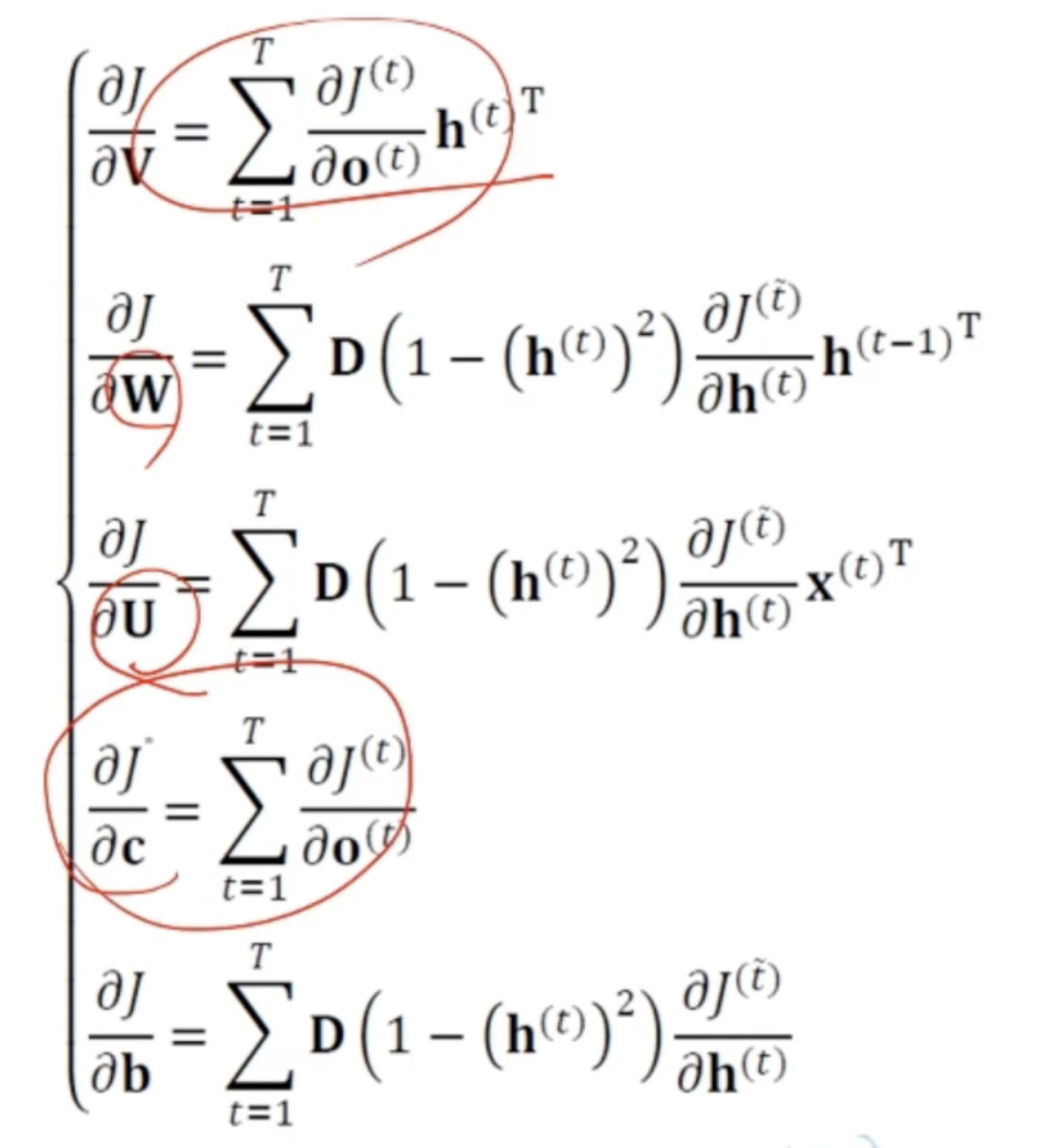
• 각 매개변수별 경사도 식을 정리하면 위처럼 정리가 됨

• 오류 역전파 수행 진행도