뉴턴 방법
테일러 급수 적용
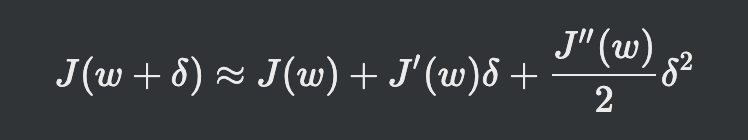
- 테일러 급수
- 주어진 함수를 정의역에서 특정 정의 미분계수들을 계수로 가지는 다항식의 극한(멱급수)으로 표현함

- 변수가 여러개일때 (H는 헤시언Hessian행렬)
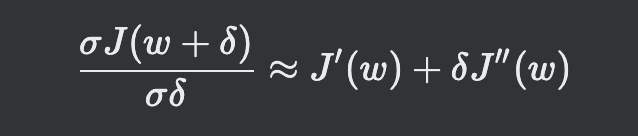
- 델타로 미분하면 이런 식이 나오게 되고

- w + 델타 값을 최소점이라고 가정한다면
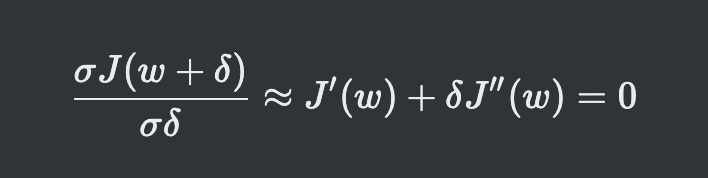
- 기울기는 0값으로 판단
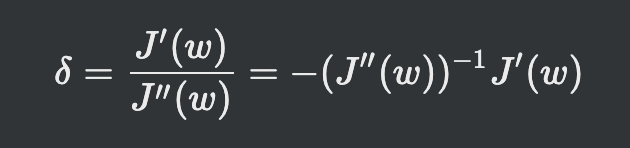
- 식을 델타에 대한 식으로 정리하고

- 변수가 여러 개인 경우로 확장하면 위의 식으로 정리됨
뉴턴 방법 실제 계산
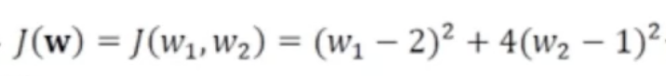
- 주어진 함수의 그래디언트와 헤시언 행렬을 구하면
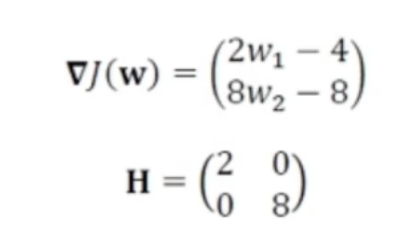
- 이런 식으로 정리됨

-
(4,2)^T 를 현재점 w1이라고 하면 w1에서 그래디언트는 (4,8)^T 이다
-
이걸 식에 대입하면 이런식으로 나옴
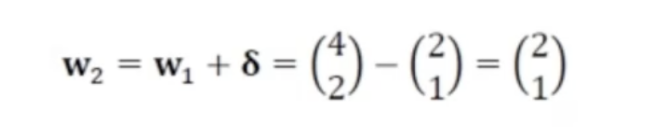
- w2는 위의 식으로 정리될 수 있고 이 점은 최저점임을 알 수 있다
뉴턴 방법의 적용
- 실제 사용하는 목적함수는 2차 함수보다 복잡한 함수라 한번에 최적해에 도달 불가능
- 반복하는 뉴턴 방법을 사용해야함
- H 헤시언을 구하는 과정에서 O(n^3) 시간복잡도가 걸림
- 결레 경사도 방법이 대안 제시
