Convolutional Neural Networks

Hyunsoo Lee·2022년 12월 29일

Basics of ML & DL

목록 보기

5/5

이 자료는 인공지능 교육 비영리단체 OUTTA 에서 출판한 《인공지능 교육단체 OUTTA 와 함께 하는! 머신러닝 첫 단추 끼우기》 를 바탕으로 제작되었습니다.

Remnote 자료는 링크를 통해 확인하실 수 있습니다.

Made by Hyunsoo Lee (SNU Dept. of Electrical and Computer Engineering, Leader of Mentor Team for 2022 Spring Semester)

5.1. 컴퓨터가 이미지를 인식하는 방식

5.1.1. 비트맵 이미지

각 위치의 픽셀들이 어떤 색상 정보를 담고 있는지 저장
흑백 이미지의 경우?
- 검은색 0, 흰색 255를 기준으로 정도를 표현
이미지가 흑백이 아닌 경우?
- 빛의 3원색 (R, G, B) 이용
- 이미지가 흑백이 아닌 경우, 색을 만들어내는 데 빛의 삼원색(빨강, 초록, 파랑)을 얼마나 합성시켜야 하는지를 나타내면 된다. 각각의 색이 합성되는 정도를 표현할 때, 합성되지 않음을 0으로, 최대한으로 합성됨을 255로 나타낸다.
채널
- 이미지를 구성하는 요소, 색상과 같은 의미 (R/G/B 채널)
- 이미지 픽셀을 입력으로 받아, 출력으로 픽셀을 내보내는 사상 (Mapping)
- 이미지로부터 추출할 수 있는 어떠한 정보를 격자 형태로 배열해둔 것

5.1.2. 벡터 이미지

점들을 연결하여 선을 만들고, 선들을 연결하여 면을 형성되는 정보 자체를 저장하는 방식

5.2. 밀집 신경망에서 CNN으로

이미지 처리 분야에 밀집 신경망 (FC Layer)이 사용 불가능한 이유?
- 밀집 신경망의 경우 1차원으로 입력을 받음
  - 2차원 데이터의 경우 Flatten 된 형태로 입력됨
- 즉, 이미지의 공간적 정보를 나타내지 못함!
- CNN : 공간적 정보를 유지하며 학습하는 신경망

5.3. CNN의 구조

Convolutional Neural Networks 를 소개한 'An Introduction to Convolutional Neural Networks' 라는 논문에서는 아래와 같은 구조를 제시하였다.

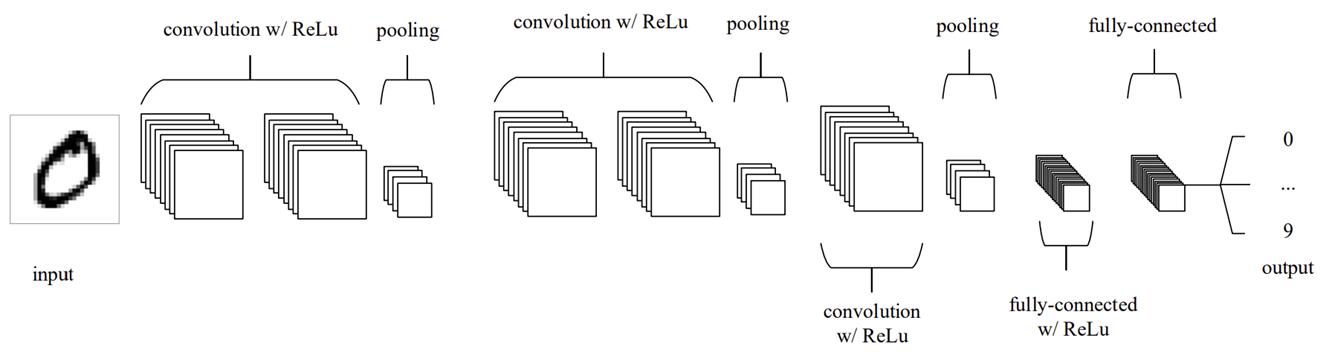
Figure source : O'Shea, K. & Nash, R. (2015).

Convolution + ReLU + Pooling 이 총 3번 이루어진 후, 출력층으로 FC Layer 를 사용하고 있다.
이 외에도, 다양한 논문에서 Convolution Layer 를 이용한 모델 구조를 제시하였다.
1. AlexNet
  
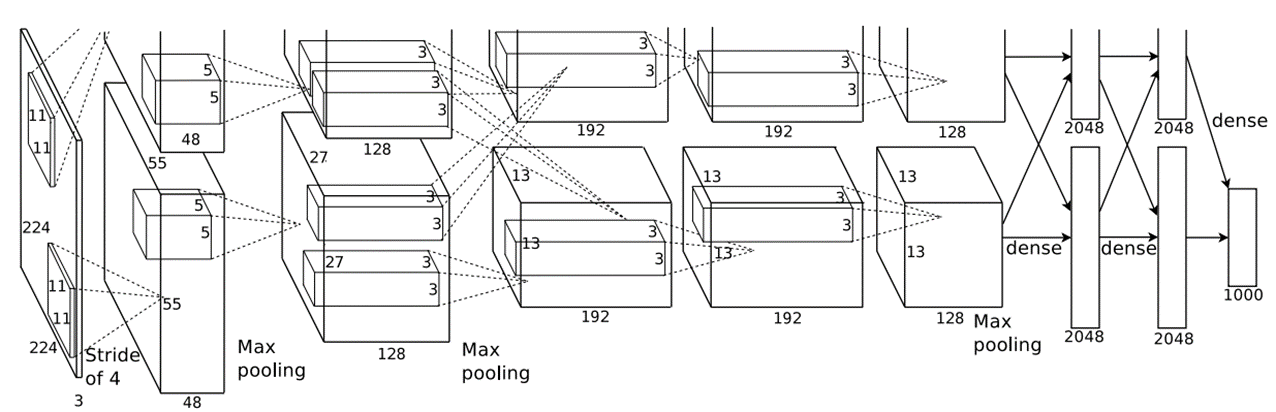
  Figure source : Krizhevsky, A., Sutskever, I. & Hinton, G. E. (2012).
2. GoogleNet
  
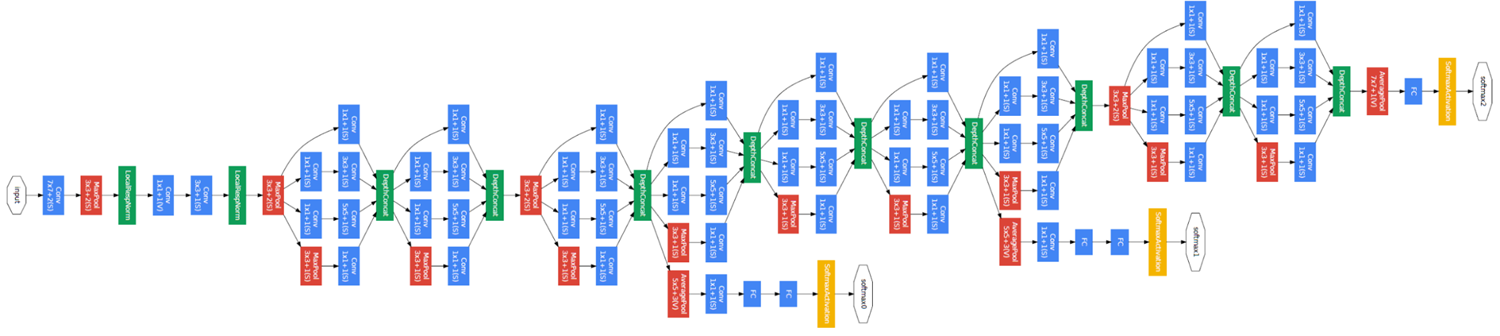
  Figure source : Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V. & Rabinovich, A. (2015)

5.4. 합성곱 신경망

5.4.1. 1개 채널에 대한 Convolution

필터 (Filter) = Kernel
- "합성곱 연산을 수행시킬 필터" 를 의미한다. 필터의 채널이 1개임을 확인하자.
- Filter Size : Hyperparameter
Convolution 연산
- 수학적 정의
  $(f*g)(x) = \int_{-\infin} ^{\infin} f(t)g(x-t)dt$
- 신경망에서의 정의
  
  입력값 A, 필터 B 에 대해 Convolution 연산 A ◎ B 를 수행해보자. Stride = 1 로 가정하자 (Stride 는 필터 연산을 적용할 위치의 간격으로, 자세한 내용은 잠시 후에 설명한다).
  
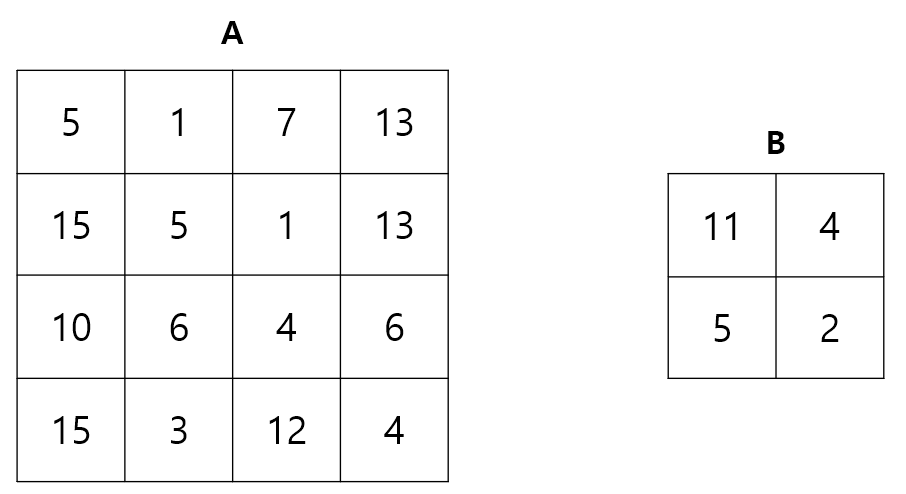
  입력값 A의 왼쪽 상단부터, B를 포개고 원소별 곱을 계산한 후 이를 모두 더한 값을 계산한다. 이후, 행렬 B를 오른쪽으로 1칸씩 이동시키고, 더 이상 오른쪽으로 이동할 수 없다면 한 줄 아래의 맨 왼쪽위치로 이동시킨 뒤 동일한 작업을 반복한다. 처음 3단계를 나타내면 아래 그림과 같다.
  
  Step 1.
  
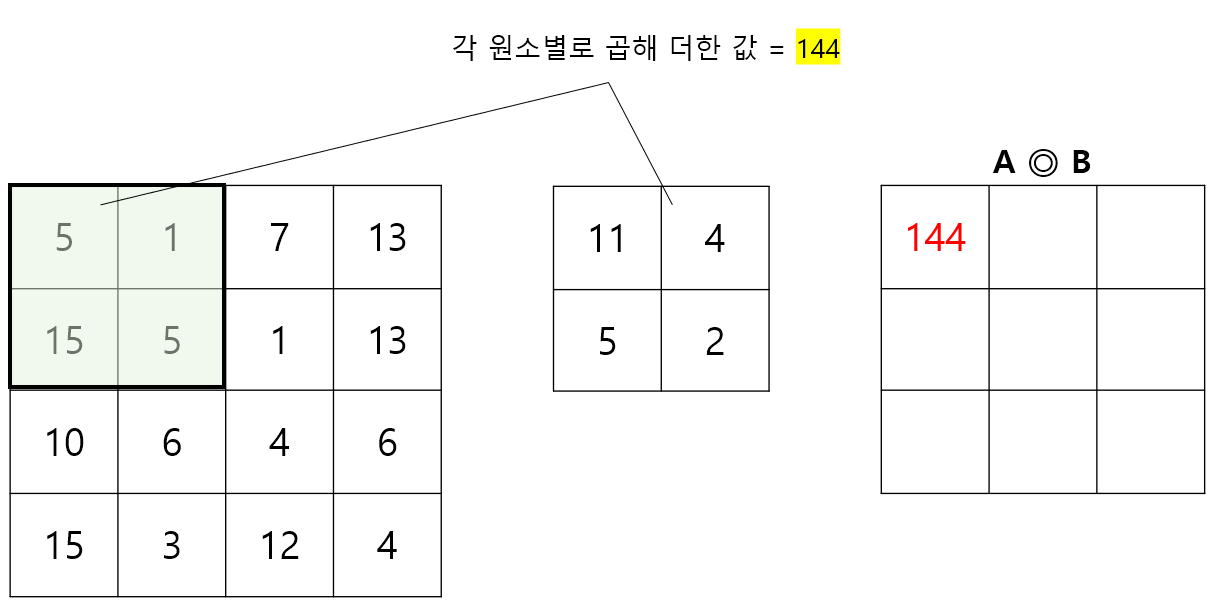
  Step 2.
  
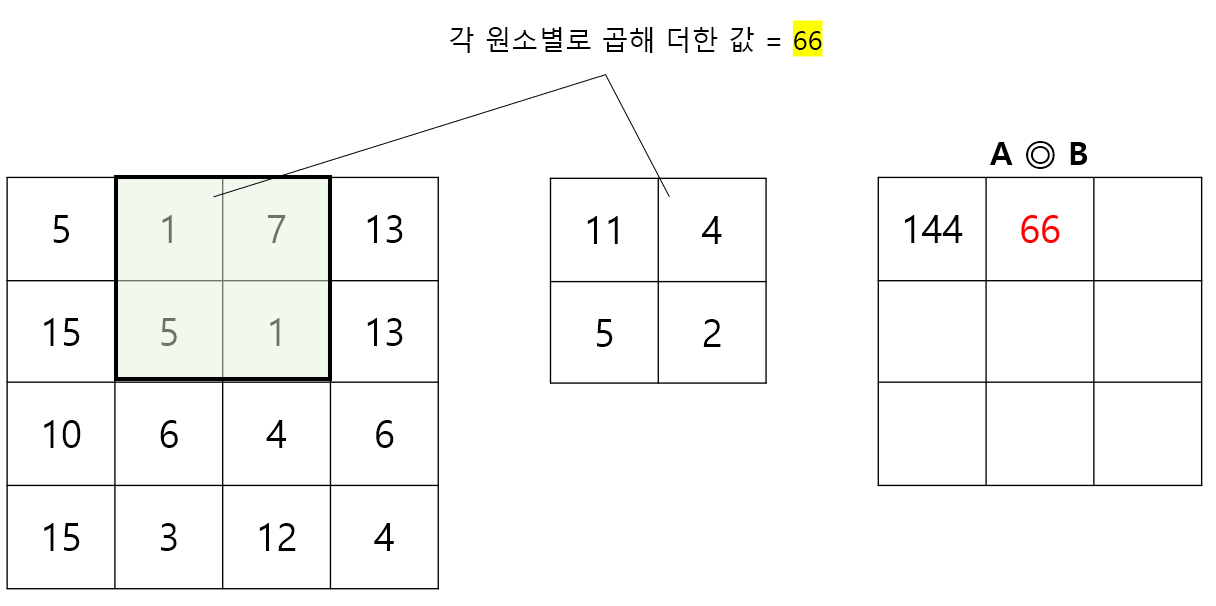
  Step 3.
  
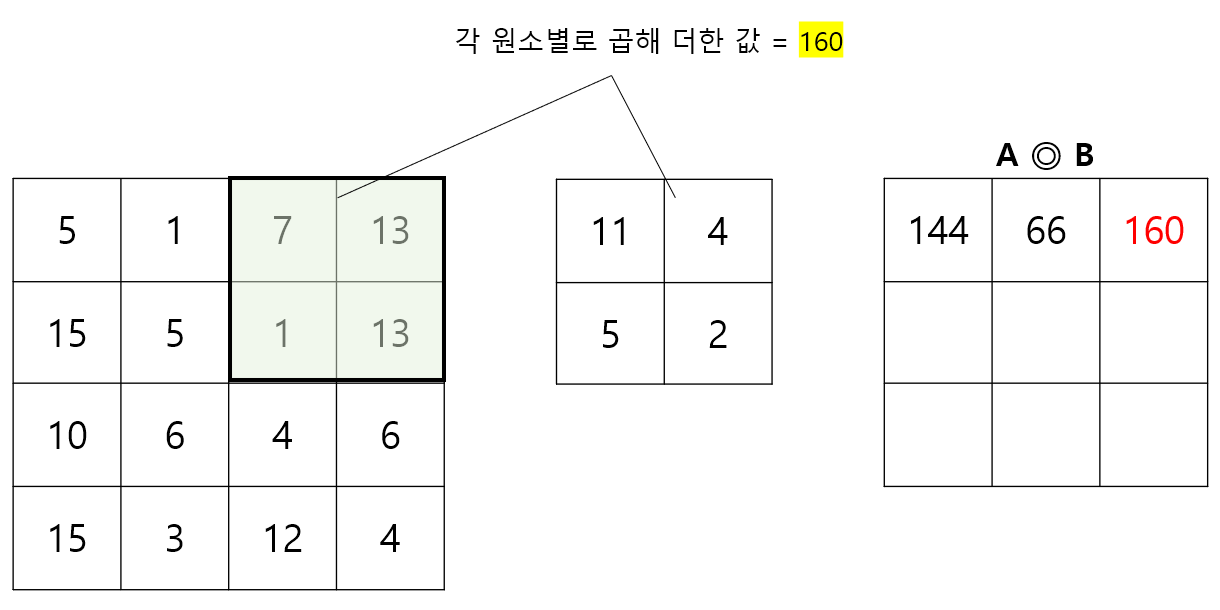
  위 과정을 반복하면 최종적으로 다음과 같은 결과를 얻을 수 있다.
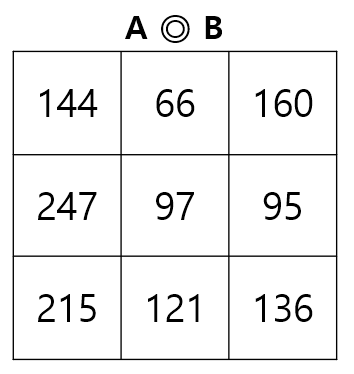
  - 편향 (bias)이 존재하는 경우 : 편향이 더해지는 방식에 유의하며 아래 그림을 살펴보자.
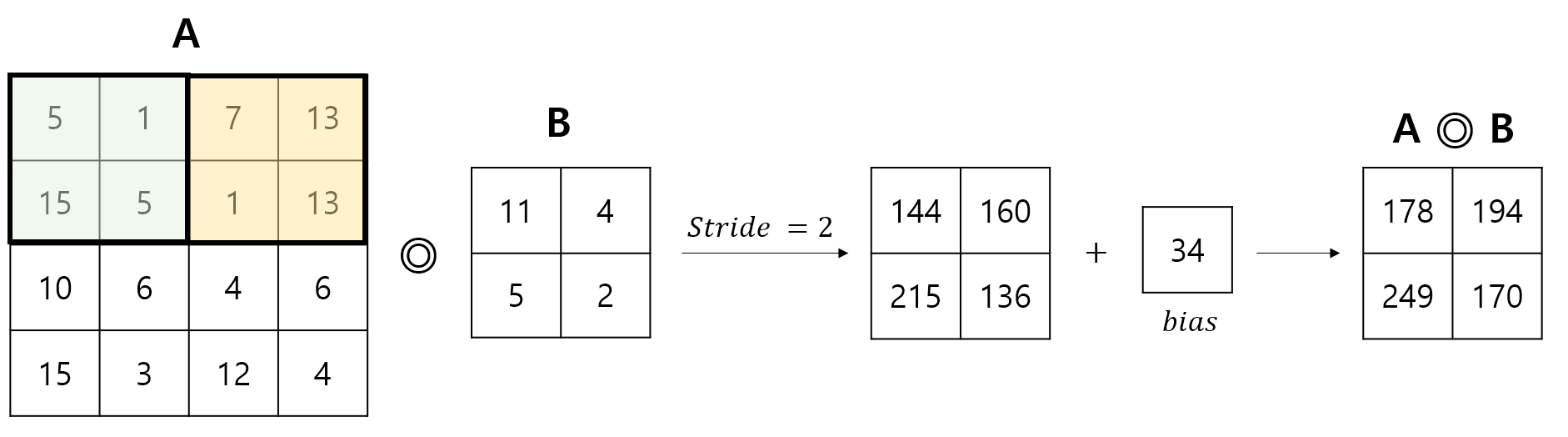
  - 지금까지 2차원 행렬 A, B 에 대한 Convolution 연산이 어떻게 이루어지는지 살표보았다. 이 과정을 Python 으로 구현하면 아래와 같다. 아래 구현은 Numpy 를 이용해 scratch 부터 구현한 것으로, 가장 효율적인 구현 방식은 아니다.
```
def calculate(arrayA, arrayB, bias):
  arrayC = np.zeros((arrayA.shape[0] - arrayB.shape[0] + 1, arrayA.shape[1] - arrayB.shape[1] + 1))
  for i in range(arrayA.shape[0] - arrayB.shape[0] + 1):
      for j in range(arrayA.shape[1] - arrayB.shape[1] + 1):
          for k1 in range(arrayB.shape[0]):
              for k2 in range(arrayB.shape[1]):
                  arrayC[i][j] += arrayA[i+k1][j+k2] * arrayB[k1][k2]
  arrayC += bias
  return arrayC
```
Stride
- Filter 가 이동하는 칸 수 (필터 연산을 적용할 위치의 간격)
- Stride = $1$ 의 경우
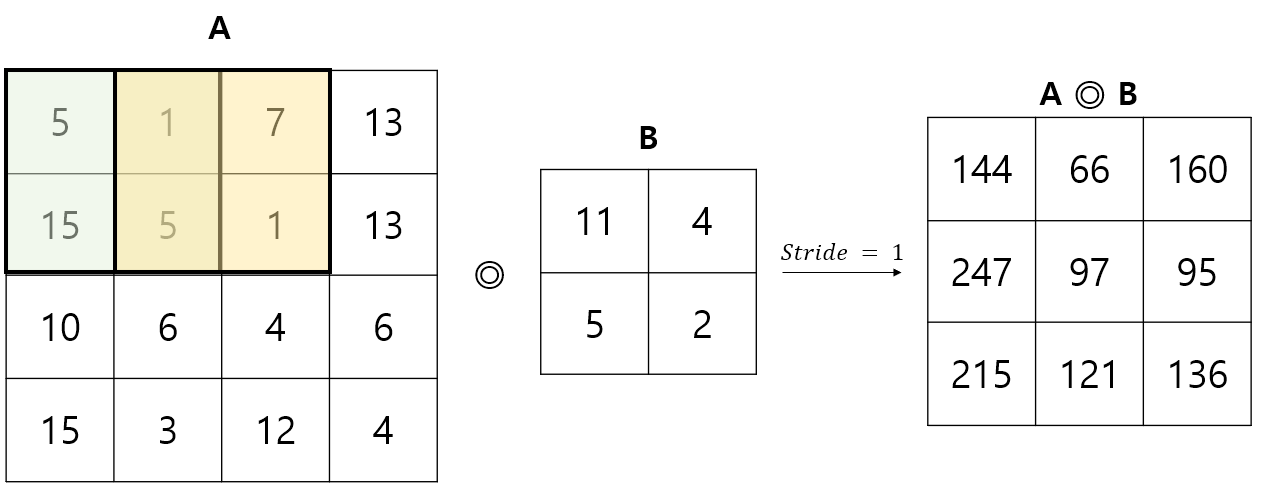
- Stride = $2$ 의 경우
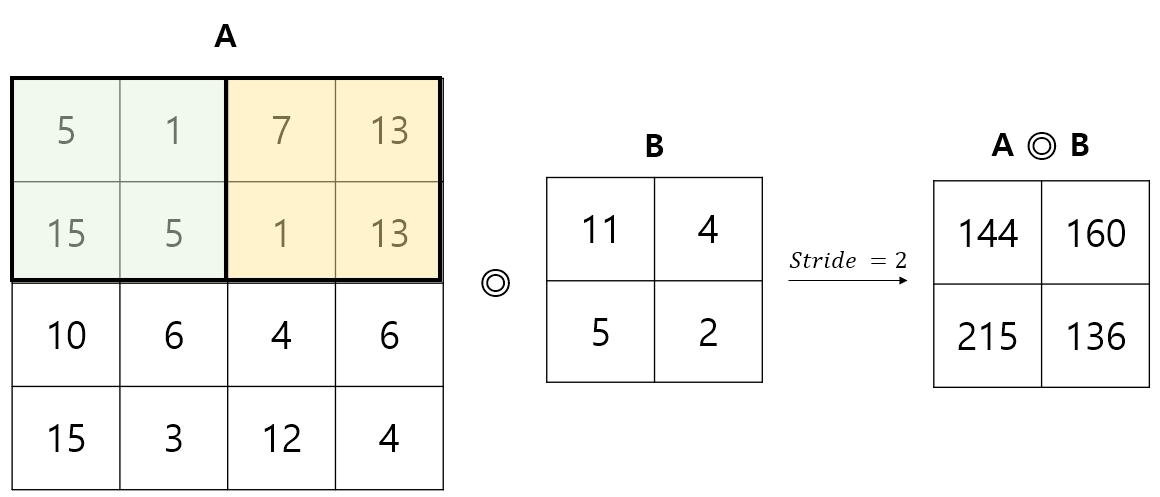
Padding
- 가장자리쪽의 픽셀은 이미지 안쪽의 픽셀보다 Filter가 거쳐 가는 횟수가 적음
- 따라서 가장자리 데이터는 합성곱 신경망의 순전파를 진행할 때 약하게 전달될 것이며, 가장자리에 중요한 데이터가 포함되는 경우 학습 효율에 악영향을 미침
- 패딩 : 합성곱 연산을 거치기 전, 입력 데이터 주변을 특정 값 (0)으로 적절히 채워 넣는 기법
- 패딩을 사용한 후, 동일한 필터 연산을 수행하면 입력 데이터의 가장자리와 내부 픽셀은 동일한 횟수의 필터 연산을 거치게 됨
- 패딩의 이점 (2가지)
  1) 가장자리 정보 소실 방지
  
  2) 입력 이미지의 크기를 증가시키는 효과 ⇒ 출력값의 Size가 너무 작아지는 문제 방지
출력값의 Shape 계산하기
- 입력값의 (채널 1개 당) Shape : $(H_{in}, W_{in})$
- Filter Shape : $(f_1, f_2)$
- Padding : $P$
- Stride : $S$
- 출력값의 Shape : $(H_{out}, W_{out})$
  
  $H_{out} = \frac{H_{in} + 2P - f_1}{S} + 1$
  
  $W_{out} = \frac{W_{in} + 2P - f_2}{S} + 1$
  - cf) Stride 역시 가로/세로 방향에 대해 다르게 설정할 수 있다. 여기서는 각 방향으로 움직이는 정도가 같다고 가정하고 공식을 유도하였다.

5.4.2. 2개 이상의 채널로 표현되는 이미지에 대한 Convolution

입력받는 데이터 채널 수와 필터 채널 수를 동일하게 설정
- ex) RGB : 입력 데이터 채널 3개 $\rightarrow$ 필터 채널 3개
필터 개수는 1개 / 채널 수 3개 (두 개는 다른 개념이므로 주의할 것!)
- Tensor 형태로 나타낸다면 Filter 의 Shape 는
  $1 \times 3 \times f_1 \times f_2$
예를 들어, 아래와 같은 연산을 생각해보자. 필터의 개수는 1개이고 (B), 입력값과 필터 모두 3개의 채널을 가진다.

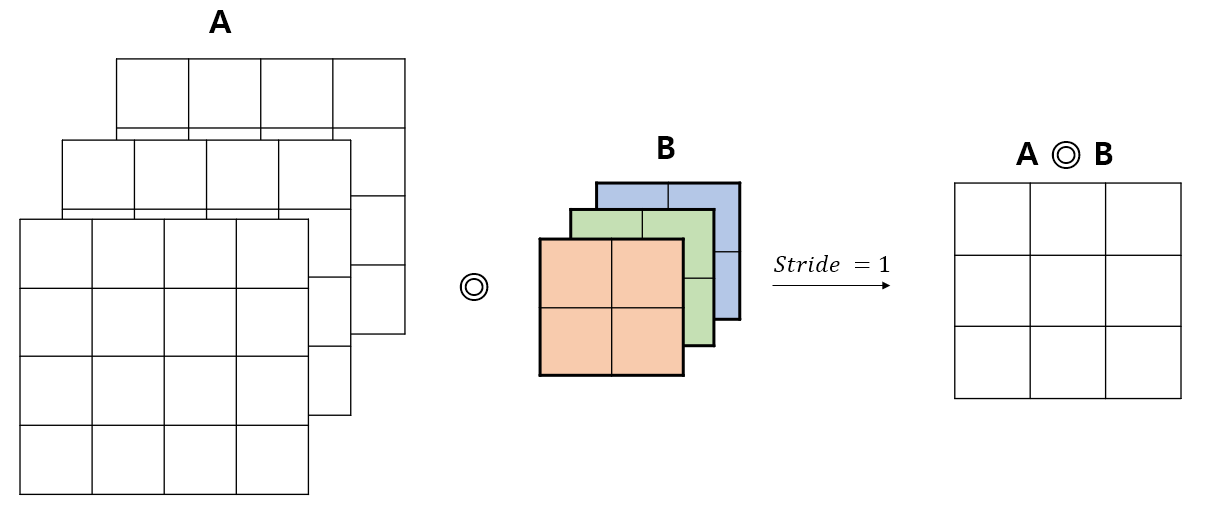
이 때 연산은 다음과 같이 수행된다. 컨볼루션 연산이 각 채널별로 이루어진 후, 동일한 위치 (이미지의 경우 픽셀) 에 대응되는 값들이 모두 더해져 채널이 1개인 결과값을 산출한다. 아래 그림을 통해 이해해보자.

Step 1.

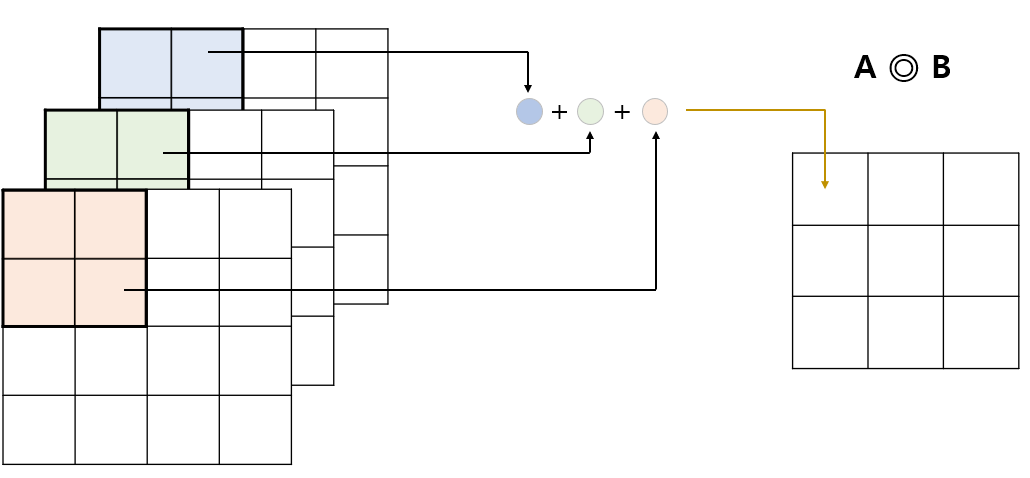
Step 2.

$\vdots$
Step 9.
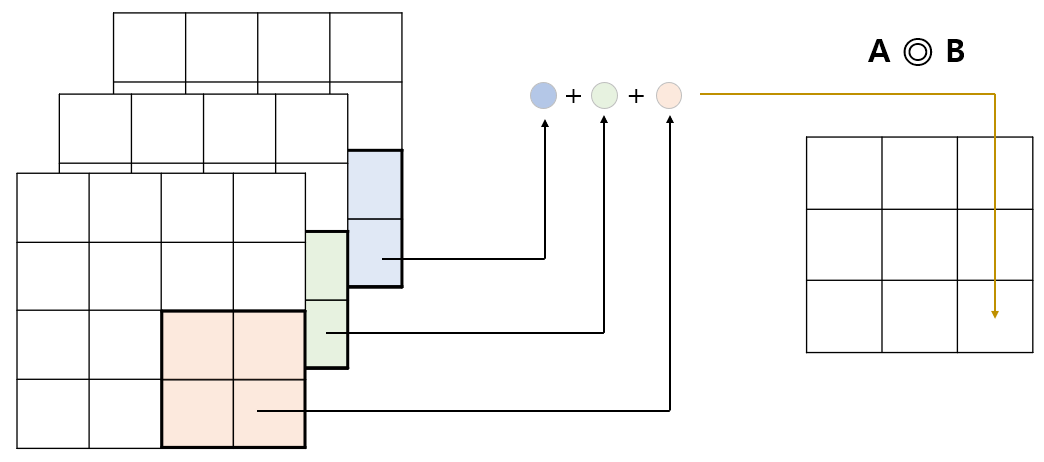
편향이 존재하는 경우 : 이 경우에도 편향은 스칼라이다. 필터 1개마다 고유한 편향 값을 가지게 되며, 필터의 채널 수에는 의존하지 않는다. 마지막에 편향 (스칼라) 값이 A ◎ B 값에 더해진다. 즉, 편향이 더해지는 방식은 필터의 채널이 1개인 경우와 동일하다.

5.4.3. 여러 개의 필터를 사용하는 Convolution

필터 하나에 대해 합성곱 연산을 적용한다면 채널이 1인 출력값을 얻음
- 입력값의 Shape 가 $(C_{in}, H, W)$ 이고 Filter 1개의 Shape 가 $(C_{in}, H, W)$ 이라면, 각 채널별로 컨볼루션 연산을 진행한 뒤 같은 위치(픽셀)의 값들을 모두 더하게 됨. $\rightarrow$ 이게 채널이 1인 출력값이 되는 것이다.
- Filter 의 개수가 여러개일 경우, 이러한 작업이 Filter 의 개수만큼 일어나고 각각의 결과들이 모아지게(Concat) 된다. 아래의 '필터 뱅크' 설명을 참고하자.
필터 뱅크 (Filter Bank) : 여러 개의 필터를 모아 놓은 것
- 입력값의 Shape 가
  $(C_{in}, H, W)$
  이고 이 입력값들에 대한 필터 1개의 Shape가 $(C_{in}, f_1, f_2)$ 일 때, 필터가 $N$ 개 있다면 Filter Bank 의 Shape 는
  $(N, C_{in}, f_1, f_2)$
  가 된다. 이 때 출력값의 채널 수는 $N$ 이 되므로, $N=C_{out}$ 이다. 결과적으로 Filter Bank 의 Shape 는 아래와 같이 표현할 수 있다.
  $(C_{out}, C_{in}, f_1, f_2)$
  이 때 출력값의 Shape는
  $(C_{out}, H_{out}, W_{out})$
  이 되며 $(H_{out}, W_{out})$ 의 값은 위에서 정의한 것과 같이
  $H_{out} = \frac{H_{in} + 2P - f_1}{S} + 1$ $W_{out} = \frac{W_{in} + 2P - f_2}{S} + 1$
  이다.
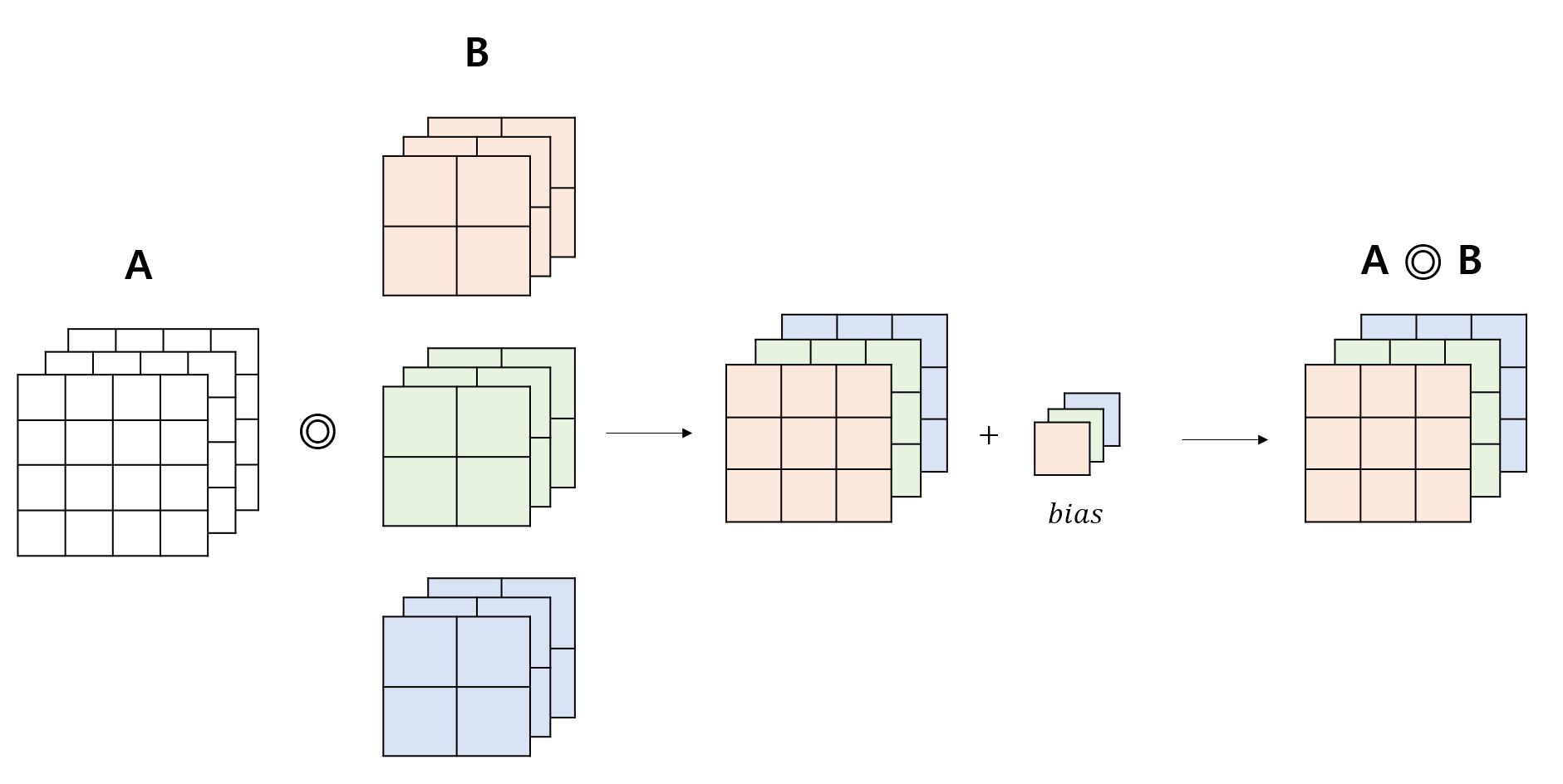
예를 들어 아래와 같이 3개의 필터를 사용하는 Convolution 연산을 생각해 보자. 각 필터는 3개의 채널로 이루어져 있다. 출력값의 채널 수는 필터 수와 동일하게 3개가 된다.
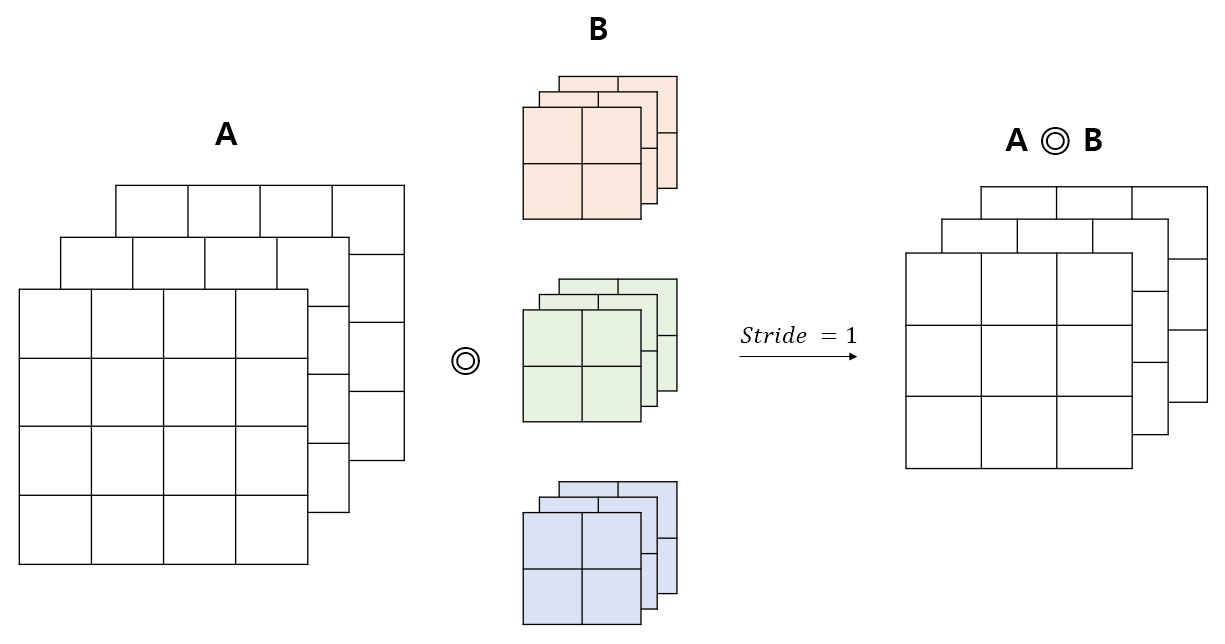
- 연산의 결과는 아래와 같다. 각각의 필터를 적용한 결과를 모아주면 (Concat) 된다.
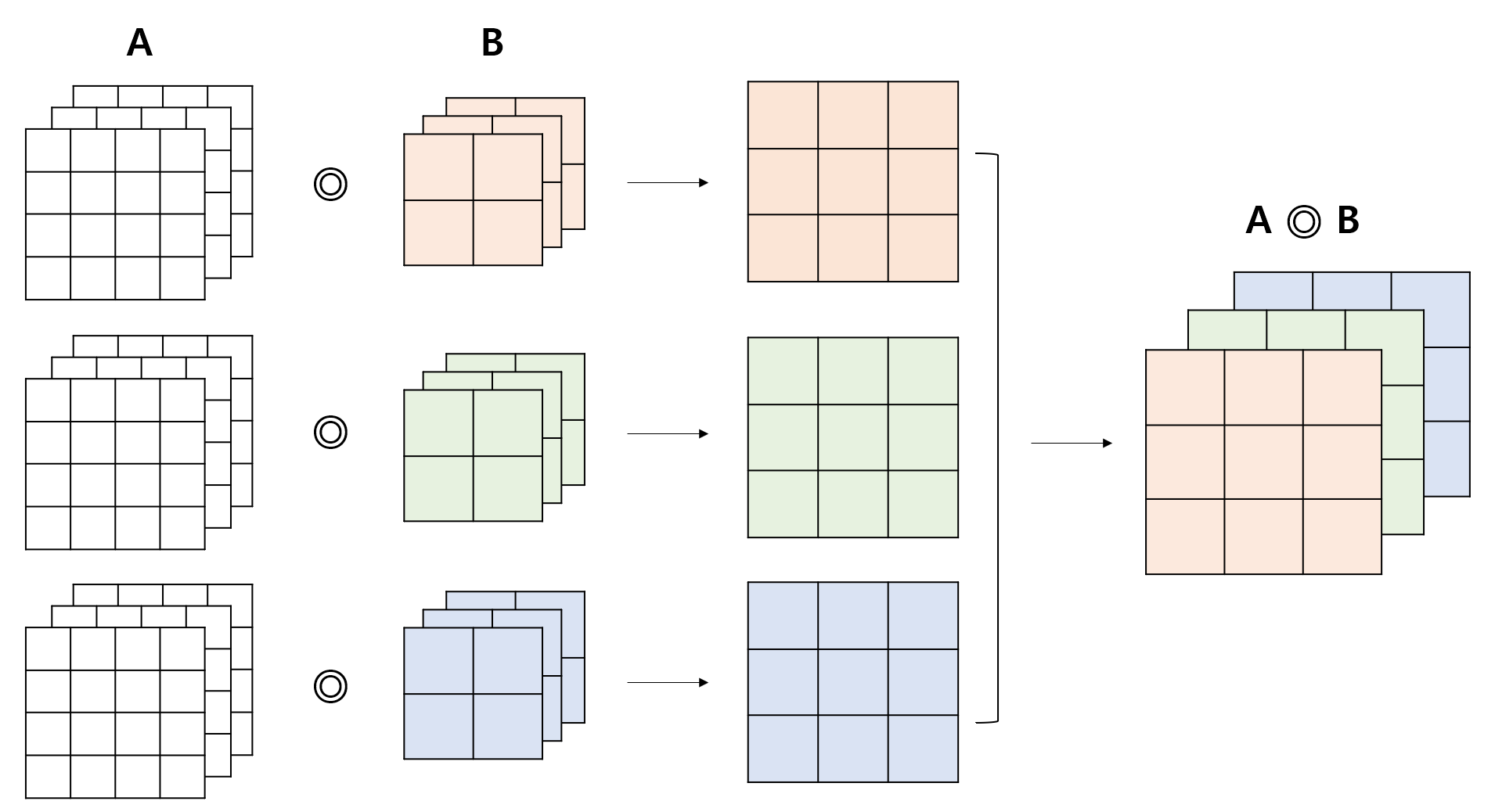
  - 편향(bias) 을 적용할 경우 그 결과는 아래와 같다. 편향의 개수가 필터의 개수와 같음에 유의하자.
  - 정리하자면, 입력층에 대해 사용한 필터 수 $(N_{filter}) =$ 출력층의 채널 수 $(C_{out})$ 가 성립한다. 모델을 구현할 때 이 점을 유의하여 설계해야 한다.

합성곱 신경망의 가중치가 Update 되는 방식 : 필터와 편향값의 가중치가 갱신됨

지금까지 5.4. 절에서는 신경망에서 일어나는 2D Convolution 에 대해 알아보았다.

5.5. 풀링 계층(Pooling Layer)

데이터의 크기 (Size)를 줄이기 위해 사용하는 층
- 단, 채널 수는 변하지 않음.
별도의 학습이 일어나지 않음
- 풀링 계층의 경우 학습 가능한 (Trainable) 파라미터가 없음.
$n \times m$ 풀링 : $n \times m$ 영역을 그 영역을 대표하는 원소 하나로 축소하여 나타내는 연산
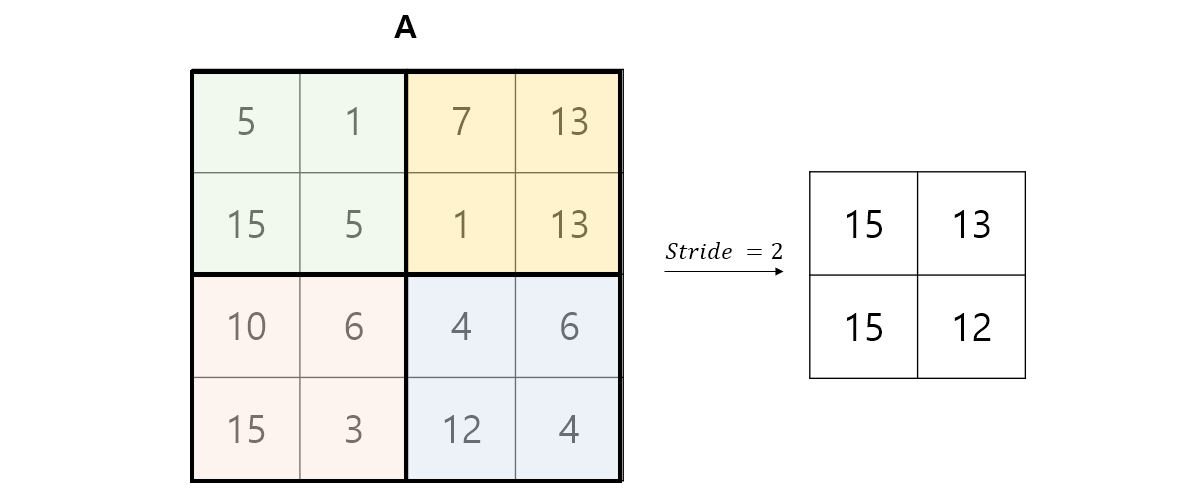
- Max Pooling
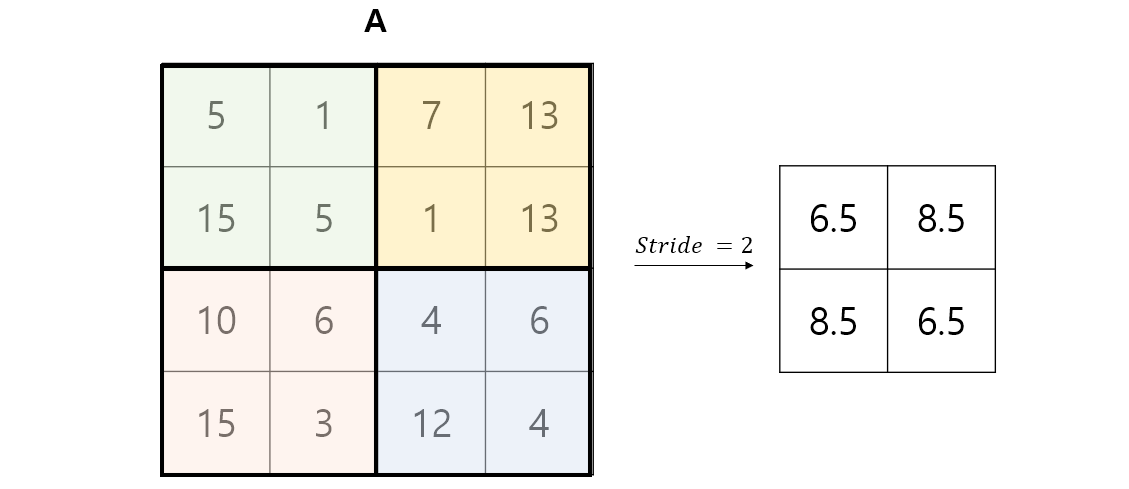
- Average Pooling

입력 데이터의 변화에 민감하지 않다. 이유는,
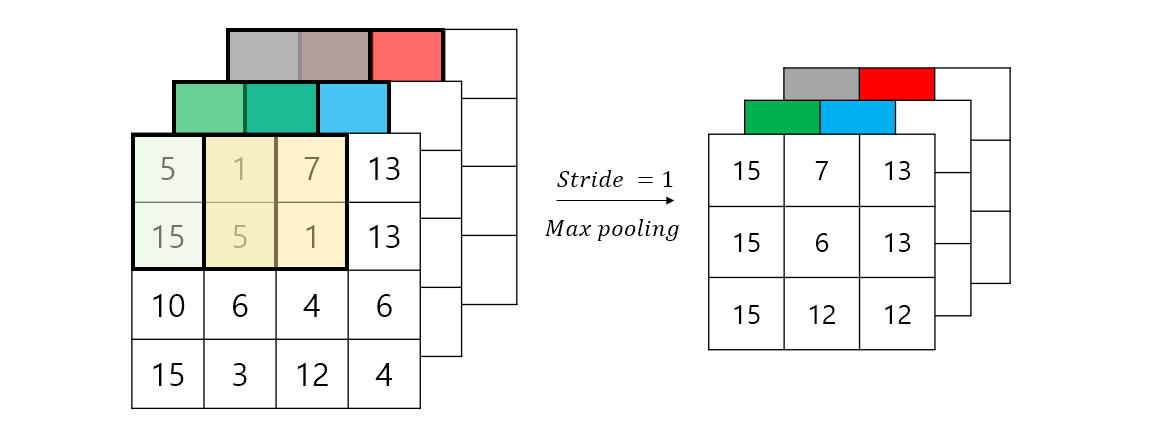
- Max pooling 을 수행하는 경우 최댓값이 변화하지 않는 이상 결과값은 그대로일 것이며, Average pooling 을 수행하는 경우에도 값의 변화가 평균에 반영되며 작게 나타날 것이다.
여러 채널의 데이터의 경우 : 각 채널에 대해 Pooling 연산이 진행된다.

5.6. CNN 학습시키기

순전파 과정 : 입력 ⇒ 합성곱 계층 ⇒ 활성화 함수 ⇒ 풀링 계측 ⇒ (반복)
벡터화 (Vectorization, Flatten)
- 이미지 분류 작업을 진행하기 위해, 밀집층에 입력하기 위한 형태인 일렬 데이터로 나타내는 과정
- Flatten 이후 사용하는 활성화 함수? : 소프트맥스 함수
손실함수를 통해 모델을 평가하면서, 모델 파라미터인 필터, 그리고 밀집층의 가중치와 편향을 갱신
최종적으로, 합성곱 계층에서 연산에 사용되는 필터 = 이미지의 특징을 추출해주는 필터
층 깊이에 따른 추출 정보

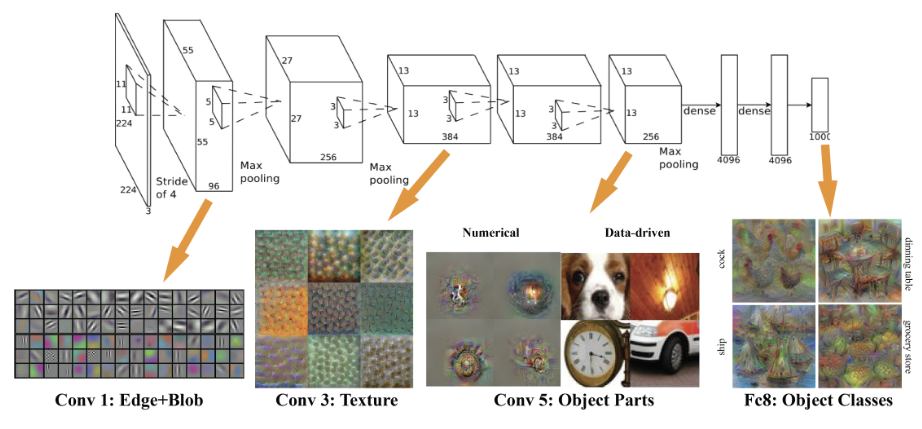
Figure source : Donglai Wei, Bolei Zhou, Antonio Torralba, William T. Freeman. (2015).
- 합성곱 계층을 더 많이 구성할수록 더 추상적인 정보를 얻을 수 있음

References

별도의 출처가 표기되지 않은 Figure의 경우 《인공지능 교육단체 OUTTA 와 함께 하는! 머신러닝 첫 단추 끼우기》에서 가져왔거나 원본을 기반으로 직접 그린 Figure 입니다.

OUTTA, 《인공지능 교육단체 OUTTA 와 함께 하는! 머신러닝 첫 단추 끼우기》
O'Shea, K. & Nash, R. (2015). An Introduction to Convolutional Neural Networks.. CoRR, abs/1511.08458.
Krizhevsky, A., Sutskever, I. & Hinton, G. E. (2012). ImageNet Classification with Deep Convolutional Neural Networks. In F. Pereira, C. J. C. Burges, L. Bottou & K. Q. Weinberger (ed.), Advances in Neural Information Processing Systems 25 (pp. 1097--1105) . Curran Associates, Inc. .
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V. & Rabinovich, A. (2015). Going deeper with convolutions. , .
Donglai, W., Bolei, Z., Antonio, T., William T, Freeman. (2015) mNeuron:A Matlab Plugin to Visualize Neurons from Deep Models, Massachusetts Institute of Technology.

Hyunsoo Lee

이전 포스트