Gradient Descent

이 자료는 인공지능 교육 비영리단체 OUTTA 에서 출판한 《인공지능 교육단체 OUTTA 와 함께 하는! 머신러닝 첫 단추 끼우기》 를 바탕으로 제작되었습니다.

Remnote 자료의 경우 링크를 통해 확인하실 수 있습니다.

Made by Hyunsoo Lee (SNU Dept. of Electrical and Computer Engineering, Leader of Mentor Team for 2022 Spring Semester)

3.1. 일반적인 상황에서의 손실함수 표기

• Model Parameters : $w_1, w_2, \cdots , w_M$
• Data points : $(x_n, y_n)_{n=0} ^{N-1}$
• Loss function : $\mathcal{L}(w_1, w_2, \cdots, w_M ; (x_n, y_n)_{n=0} ^{N-1})$

3.2. 경사하강법에 대한 정성적 설명

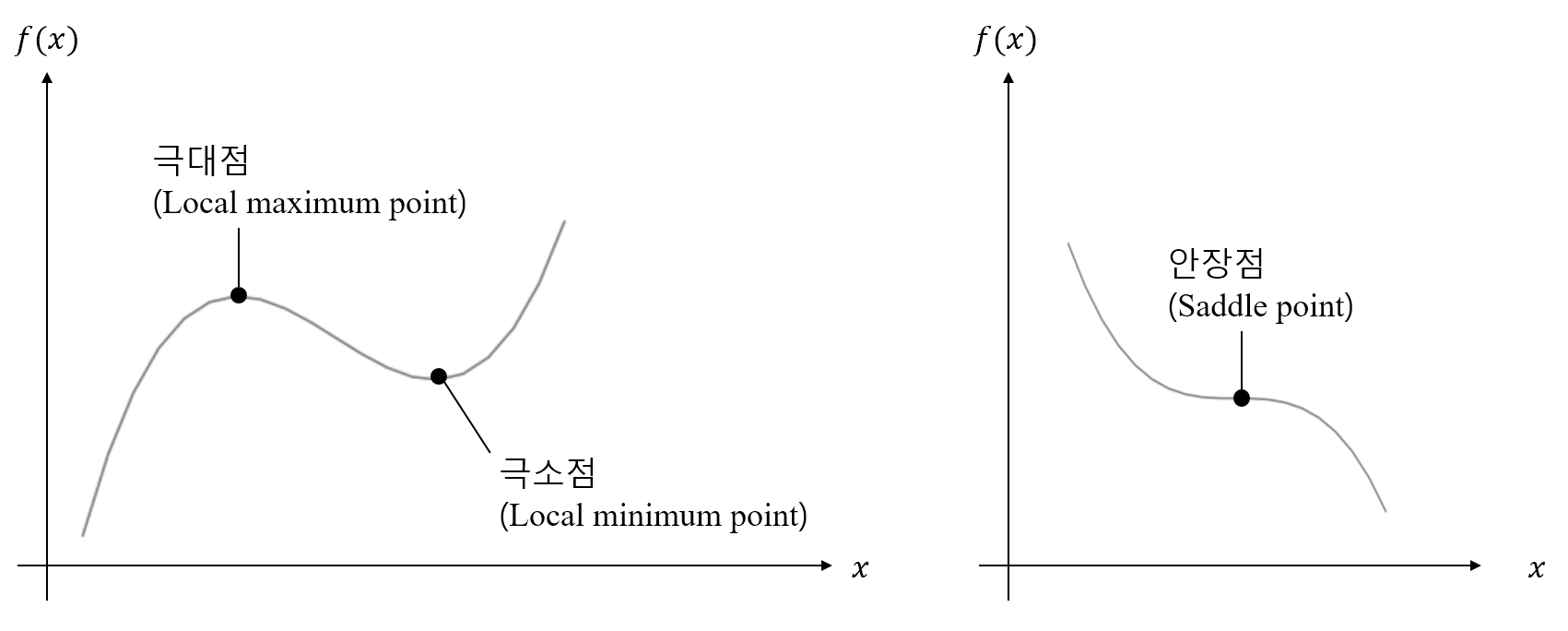
• 극소점, 극대점, 안장점

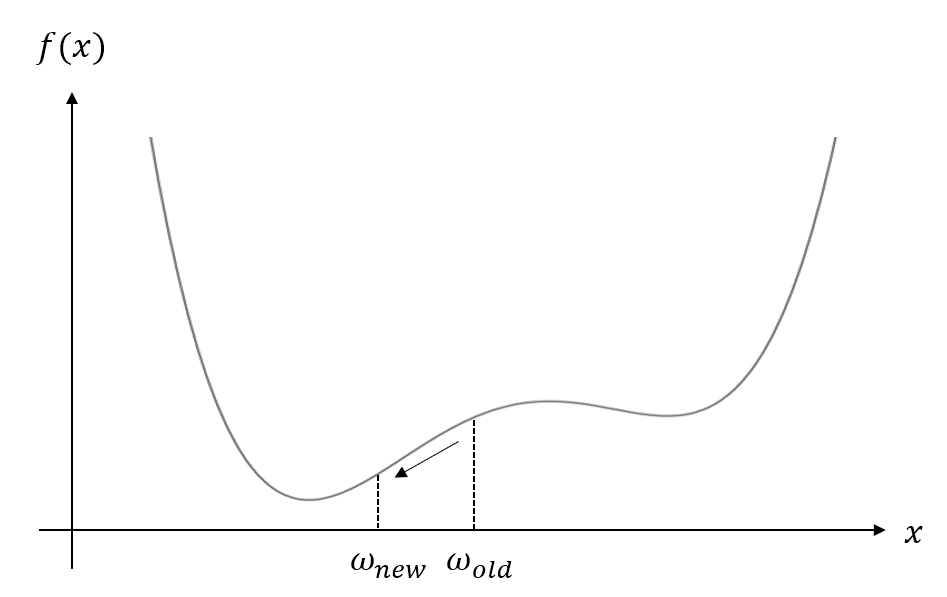
• 경사하강법의 과정 (그림)

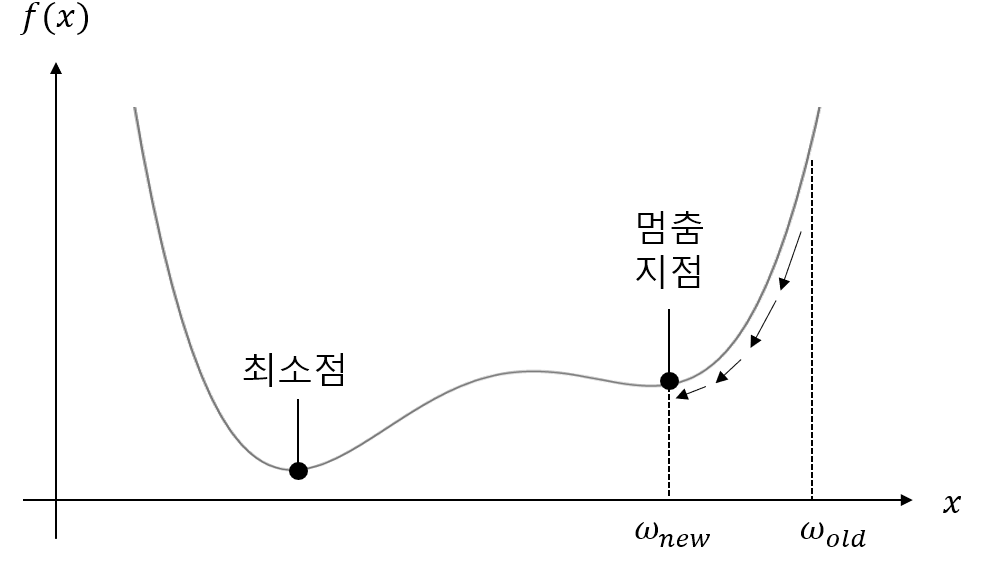
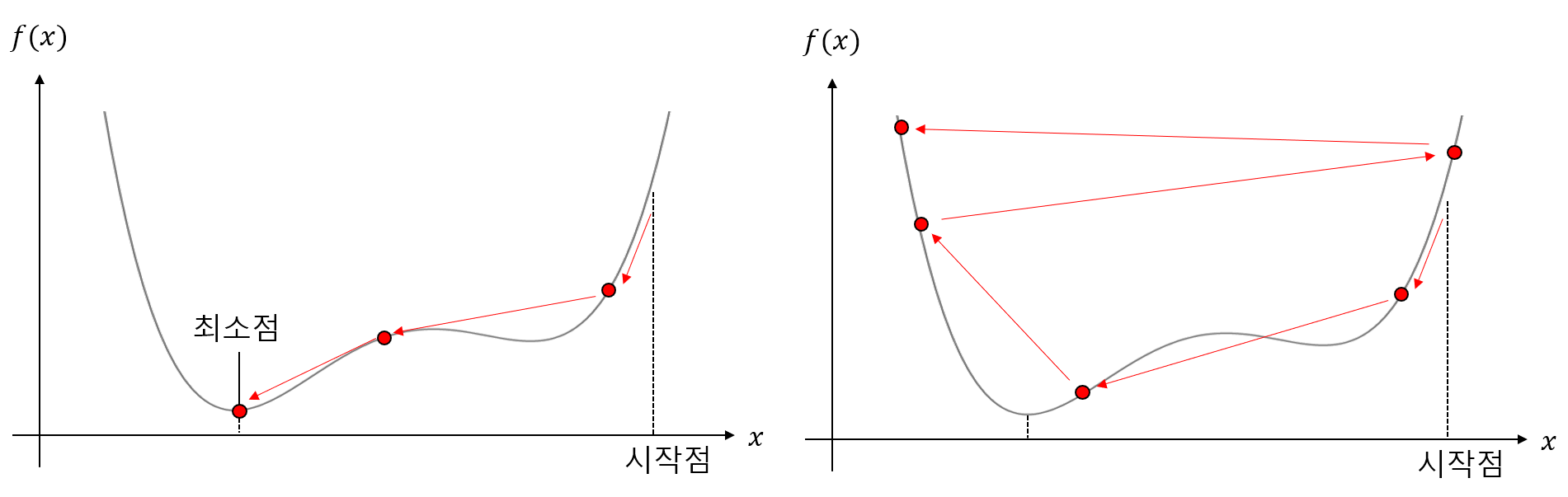
• 경사하강법에서 최소점 찾기에 실패한 경우 (그림)

3.3. 일변수함수에 대한 경사하강법

• 원리 : $\mathcal{L}(w)$ 에서 순간변화율이 음수인 경우 $w$ 증가, 양수인 경우 $w$ 감소

• One Step (Equation) :

  $w_{k+1} = w_{k} - \delta \cdot \left. \frac{d\mathcal{L}}{dw} \right|_{w = w_k}$

  • 학습률 (Learning rate, $\delta$) : 한 번의 Step 에서 가중치$(w)$ 값을 얼마나 변화 시킬지에 대한 척도

    • 적절한 학습률 값을 설정해야 한다.

      

    • 각각 적절한 학습률의 경우 (좌), 학습률이 너무 큰 경우 (우)

  • 종료 조건 : $w=w_{old}$ 일 떄 $\frac{d \mathcal{L}}{dw} \approxeq 0$

  • $w$의 출발점 (Initial Value) 역시 영향을 줌

• Example

    import numpy as np
    def descent_down_parabola(w_start, learning_rate, num_steps):
        w_values = [w_start] 
        for _ in range(num_steps):
            w_old = w_values[-1] 
            w_new = w_old - learning_rate * (2 * w_old)
            w_values.append(w_new)
        return np.array(w_values)

3.4. 다변수함수에 대한 경사하강법

• Model Parameter가 $M$개라고 가정 $(w_1, w_2, \cdots , w_M)$

• Equation for GD :

  $\textbf w_{k+1} = \textbf w_{k} - \delta \cdot \left. \nabla \mathcal{L}(\textbf w) \right|_{\textbf w = \textbf w_k}$
  $\textbf w_k= \begin{pmatrix} w_1 \\\ w_2 \\\ \vdots \\\ w_M \end{pmatrix}_k, \left. \nabla \mathcal{L}(\textbf w) \right| _{\textbf w = \textbf w_k} = \begin{pmatrix} \frac{\partial \mathcal{L}}{\partial w_1} \\\\ \frac{\partial \mathcal{L}}{\partial w_2} \\\ \vdots \\\ \frac{\partial \mathcal{L}}{\partial w_M}\end{pmatrix}_k$

• Example : $L(w_1, w_2) = 2 w_1^ 2 + 3 w_2^2$ 에 대한 GD

  import numpy as np
  def descent_down_2d_parabola(w_start, learning_rate, num_steps):
      xy_values = [w_start] for _ in range(num_steps):
      xy_old = xy_values[-1] 
      xy_new = xy_old - learning_rate * (np.array([4., 6.]) * xy_old) 
      xy_values.append(xy_new) 
      return np.array(xy_values)

  
  

3.5. 경사하강법의 하이퍼파라미터

• 경사하강법의 Hyperparameter : 1) $\textbf w_{old_0},$ 2) $\delta$, 3) Criteria for stopping 'step'

1. $\textbf w_{old_0}$

   • Gaussian Random Distribution (정규분포)으로 Randomly choose

   • 이 외에도 Xavier 초기화, He Normal 초기화 등 사용

2. $\delta$

   • Gaussian Random Distribution (정규분포)으로 Randomly choose

   • 10의 거듭제곱을 학습률로 사용해 경향 살펴보기, 이후 성능이 좋았던 값 근방의 값들에 대해 다시 성능 평가를 진행해 적절한 학습률 값 구하기

   • Example)

   

   • 위 Graph에서 Optimal 한 Learning rate $\approxeq 10^{-1}$

     • $10^{-1}$ 근방의 값 조사

       

     • Optimal Learning rate value $\approxeq 0.52$

3. 종료 조건 (Criteria for stopping 'step')

   • Gradient 의 값을 그래프에 나타낸 뒤 사용자가 판단

   • Auto-stopping option : $n$번 반복할 때 값이 변화하지 않으면 학습 종료

   • Thresholding : 특정 값 이하로 Gradient가 감소하면 종료

Reference

• OUTTA, 《인공지능 교육단체 OUTTA 와 함께 하는! 머신러닝 첫 단추 끼우기》