시계열이란?
시계열이란 일정 시간 간격으로 배치된 데이터들의 수열을 말합니다. 즉, 시간의 흐름이 포함되어 있는 데이터라고 볼 수 있겠습니다.
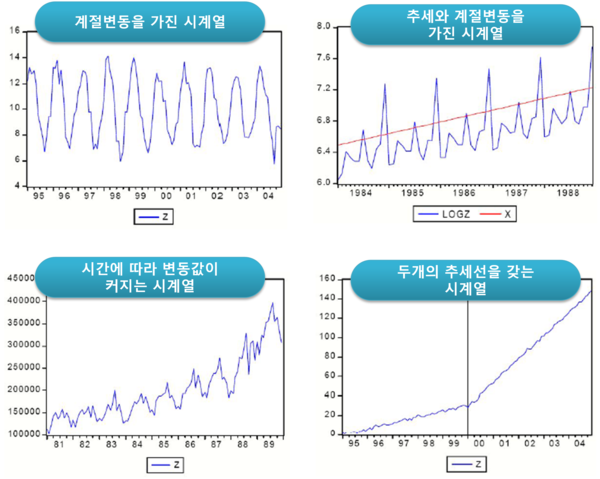
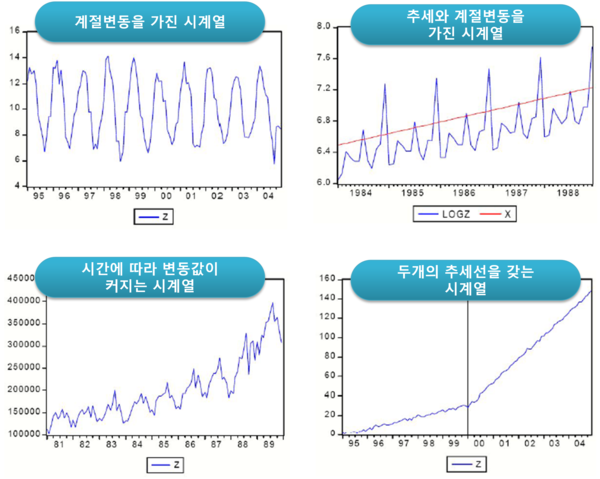
위와 같이 계절성, 추세가 있는 시계열이 있고 없는 시계열이 있습니다. 여기서 계절성과 추세가 없는 시계열을 정상성을 띠는 시계열 데이터라고 하는데 다음 글에서 더 자세히 다루겠습니다.
시계열 분석이란?
시계열 분석은 시계열 데이터와 추세 분석을 통해 쓸모 있는 정보들을 추출하는 통계 기법입니다. 시계열 데이터는 그저 시간에 따라 나열된 데이터에 불과하여 시계열 분석은 이 데이터를 이해하고 통계적인 정보들을 추출하여 미래를 예측하고 결론을 도출하는 과정 전체를 말합니다.
시계열 데이터 관련 기본 지식
1. 정상성과 비정상성
정상성이란 ARIMA 모델링을 통해 시계열 데이터를 분석할 때 필수적으로 고려해야하는 가정으로 시점에 무관하게 과저, 현재, 미래의 분포가 같을 때 정상성을 띤다 말하고 추세를 보이거나 계절성을 보이면 비정상성을 띤다고 말합니다.
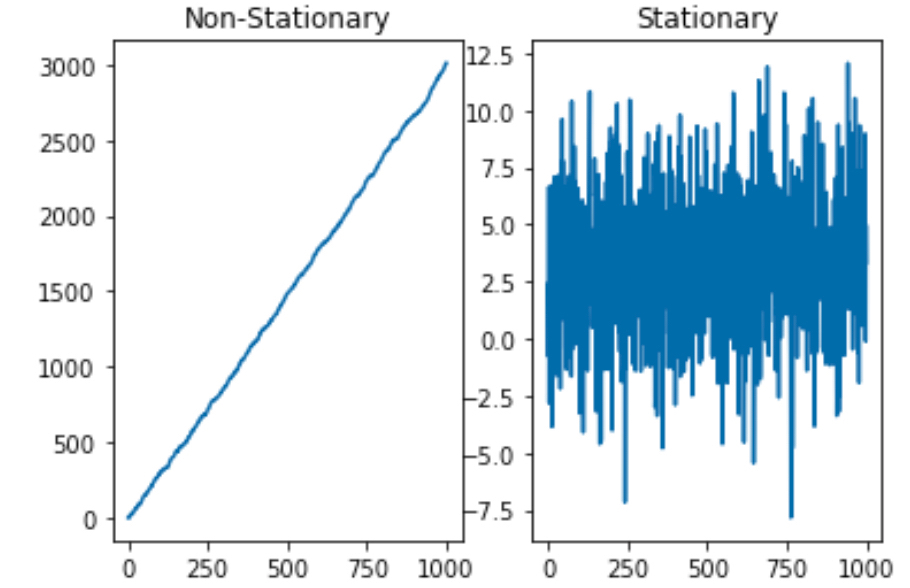
왼쪽이 비정상성을 띠는 대표적인 그래프이고 오른쪽이 정상성을 띠는 대표적인 그래프입니다.
2. 추세, 계절성, 주기성
여기서 추세란 데이터가 장기적으로 위로 올라가는지 아래로 내려가는지를 말합니다.
계절성은 해마다 어떤 특정한 때나 1주일로 봤을 때 특정 요일에 나타나는 계절성 요인을 말합니다.
주기성은 고정된 빈도가 아닌 형태로 증가나 감소하는 모습을 보일 때 '주기'라고 합니다.
계절성과 주기가 헷갈릴 수 있는데 제일 큰 차이점은 계절성은 1년 마다 같은 변화가 생기는 것이고 주기는 1년보다 길고 다양하며 변동폭이 훨씬 큽니다.
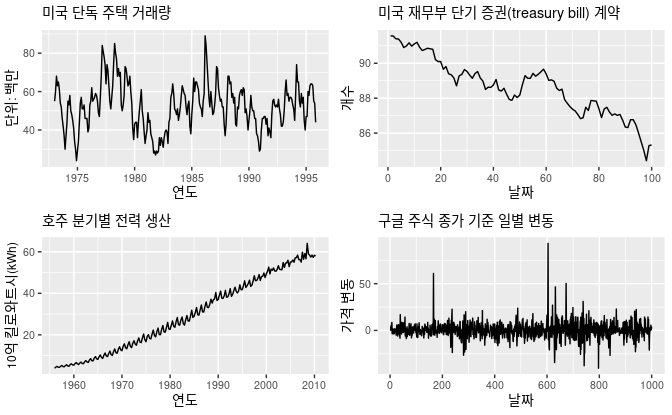
추세를 보이는 그래프: 2, 3
계절성을 보이는 그래프: 1, 3
주기성을 보이는 그래프: 1
3. 백색잡음, 확률 보행
백색잡음(white noise): 정상성을 띠는 대표적인 예로 평균이 0이고 분산이 유한한 확률분포로부터 자기상관이 없게 무작위로 추출된 시계열 데이터를 말합니다.
from random import gauss
from random import seed
from pandas import Series
import matplotlib.pyplot as plt
generator = seed(1)
series = [gauss(0.0, 1.0) for i in range(1000)] #(0,1)정규분포에서 난수 추출
series = Series(series)
print(series.describe())
series.plot()
plt.show()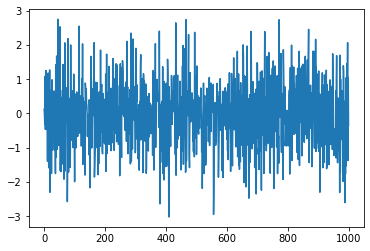
위의 백색잡음은 평균이 0이고 분산이 1인 정규분포로부터 랜덤하게 추출한 데이터로 가법 백색 가우시언 잡음이라고도 함.
확률 보행(Random Walk): 수학에서 확률보행은 어떤 수학적인 공간 (예: 정수)에서 연속적인 무작위 스텝의 이동경로를 묘사하는 수학적인 객체를 말합니다. 예시로 동전 던지기를 들자면 점수를 매길 때 앞면이 나오면 +1 뒷면이 나오면 -1로 하고 그래프를 그려보면 확률보행과정 그래프가 완성이 됩니다.
import numpy as np
probability = [0.5, 0.5] #확률
start = 0
rand_walks=[start]
rand_point = np.random.random(300)
down_probability = rand_point < probability[0]
up_probability = rand_point >= probability[1]
for down, up in zip(down_probability, up_probability):
rand_walks.append(rand_walks[-1] - down+up)#False =0 True=1인 것을 활용
plt.plot(rand_walks)
plt.show()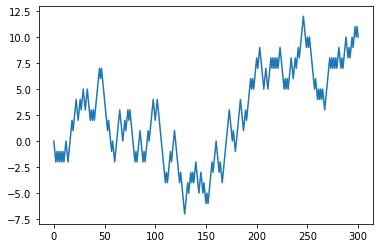
위의 사진은 확률 행보
시계열 데이터
시계열 데이터 종류: 국내총생산량(GDP), 금융데이터, 날씨 or 강수량 데이터, 소비자 물가 지수, 실업률 등이 있습니다.
또 시계열 데이터는 연속 시계열 데이터와 이산 시계열 데이터로 나누어집니다.
연속 시계열 데이터: 연속적으로 생성되는 시계열 자료로서, 관측 값들이 연속적으로 연결된 형태의 자료를 의미합니다.
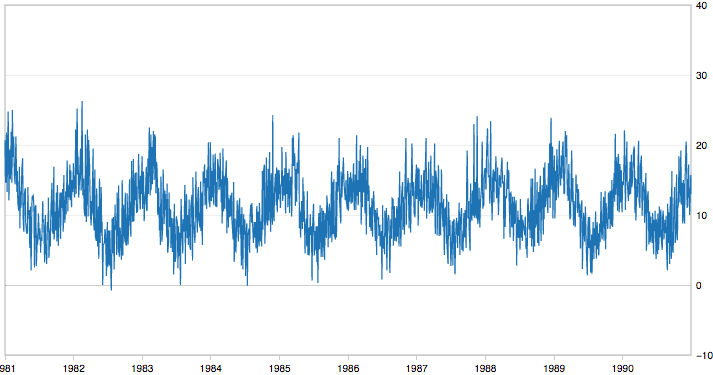
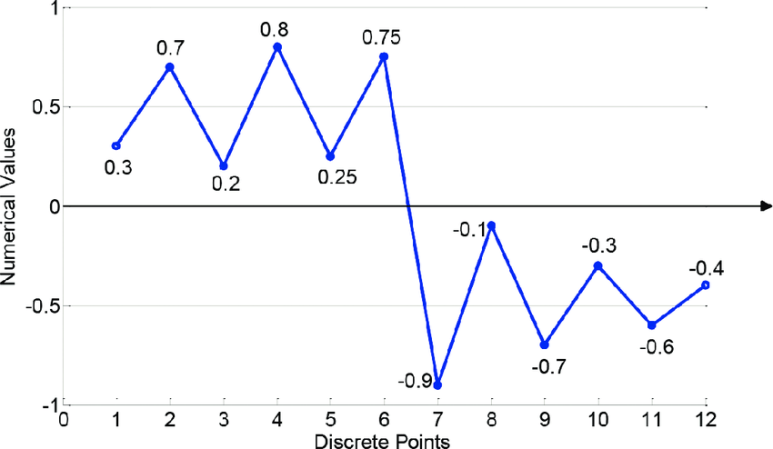
이산 시계열 데이터: 연속 시계열 데이터는 모든 시점이 연결되어 있기 때문에 분석하기 부담스러워 이산 시계열 데이터를 많이 사용한다. 이산 시계열 데이터란 특정 시점에서 측정한 관측값들의 집합을 말한다.
시계열 데이터 분석 모델 ARIMA
1. AR(Auto Regression)모델
AR은 자기회귀 모델이라고 하며 RNN과 비슷하게 이전의 값이 현재값에 영향을 미칩니다.
식은 X(t) = (X(t-1)w)+b+(e(t)u)입니다. 여기서 w=b=0이면 백샙 잡음(소음)이 됩니다.
2. MA(Moving Average)모델
MA은 이동 평균 모델로 추세(평균 또는 시계열 데이터 그래프에서 Y값)가 변하는 상황에 적합한 모델로 과거의 오차에 의존하는 모델입니다.
식은 다음과 같습니다. X(t) = (e(t-1)w)+b+(e(t)u)
AR에서의 X(t-1)이 e(t-1), 다시말해 이전 시점의 값이 아닌 이전 오차의 값이 계산에 영향을 미치는 것입니다.
3. ARMA와 ARIMA 모델
ARMA 모형은 AR과 MA를 합친 모형으로 수식 결합이 쉬운 반면 분석의 정확도와 설명력이 올라가는 장점이 있습니다.
식은 다음과 같습니다. X(t) = (X(t-1)w11) + (e(t-1)w21) + b + (e(t)*u)
ARIMA 모형은 ARMA에 Integrated(차분) 개념을 추가한 것입니다. 데이터 값이 해당 값과 이전 값 사이의 차이로 대체되었음을 나타냅니다. 보통 ARIMA(p,d,q)로 표현하는데 매개변수 값은 ACF와 PACF로 판단합니다. ARIMA에 대한 자세한 설명은 다른 글에서 다루겠습니다.
백색잡음, 확률보행 코드: https://github.com/Mujae/SGfDA/blob/main/%EB%B0%B1%EC%83%89%EC%86%8C%EC%9D%8C%2C%20%ED%99%95%EB%A5%A0%20%ED%96%89%EB%B3%B4%2C%20%EB%8B%A8%EC%9C%84%EA%B7%BC%20%EA%B2%80%EC%A0%95.ipynb
reference
http://www.sbr.ai/news/articleView.html?idxno=1608
https://blog.naver.com/kiaelf/222599060675
https://www.tibco.com/ko/reference-center/what-is-time-series-analysis
https://assaeunji.github.io/statistics/2021-08-08-stationarity/
https://otexts.com/fppkr/tspatterns.html