정상성과 비정상성
정상성은 시계열 데이터가 시점에 따라 평균이나 분산 같은 통계적 특징이 변하지 않으며 추세나 계절성이 없는 시계열 데이터일 때 해당 데이터를 말합니다. 즉, 시계열 데이터가 시점에 무관하게 과거, 현재, 미래의 분포가 같을 때 정상성을 띤다고 말합니다. 정상성의 종류로는 강한 정상성(Strict Stationarity), 약한 정상성(weak stationarity)가 있습니다.
하지만 강한 정상성은 조건이 까다롭기 때문에 정상성을 띤다는 것은 보통 약한 정상성을 말합니다. 약한 정상성 조건은 아래와 같습니다. (임의의 t, h)
- E[X(t)] = μ 평균이 변하지 않는다.
- Var[X(t)] < ∞ -> 분산이 유한하다. (분산을 표현할 수 있어야한다.)
- Cov[X(t+h), X(t)] = γ(h)
여기서 γ(h)는 자기공분산 함수(ACVF)이고 식은 공분산이 시점 t에 의존하지 않고 시차인 h에 의존함을 뜻합니다.
정상성이 왜 중요한가?
지난 글에서도 정상성을 언급하였고 이번에는 제목 자체가 정상성과 비정상성입니다. 그런데 정상성이 뭔지는 알겠는데 왜 중요한지, 어떤 역할을 하는지를 알아야 시원한 기분이 들 것 같습니다.
우선 한마디로 설명하자면 시계열 데이터가 정상성을 띠고 있어야 ARIMA 분석을 통해 미래 시계열 값을 예측할 수 있기 때문입니다.
아마 여기서 의문이 생기실 것 같습니다. 저도 처음 정상성 개념을 접했을 때 "정상성을 띠는 대표적인 백색잡음 그래프를 보니깐 모양도 이상하고 정상성의 조건이 '추세나 계절성 같은 패턴이 없는 것'이라고 봤는데 추세나 계절성이 있어야 분석이 쉬운 거 아님?" 같은 생각을 했었습니다. 그런데 만약 시계열 데이터가 비정상성을 띤다면 평균과 분산이 다르기 때문에 임의의 시점 t-1, t에서 얻은 모델은 t+1~t+n에서 사용할 수 없게 됩니다. 즉, 미래의 값을 예측할 수 없게 되는 것입니다. 또한 이는 회귀분석을 기반으로 데이터 분석을 하기 위함이지 패턴이나 다른 분석기법으로 예측할 때는 정상성을 고려하지 않아도 됩니다.
정상성 판단 방법
이렇게 중요한 정상성을 판단하는 방법은 대표적으로 2가지가 있습니다.
하나는 그래프(직관적인 방법 or ACF or PACF)로 판단하는 방법이고 다른 하나는 가설 검정(단위근 검정)입니다.
그래프
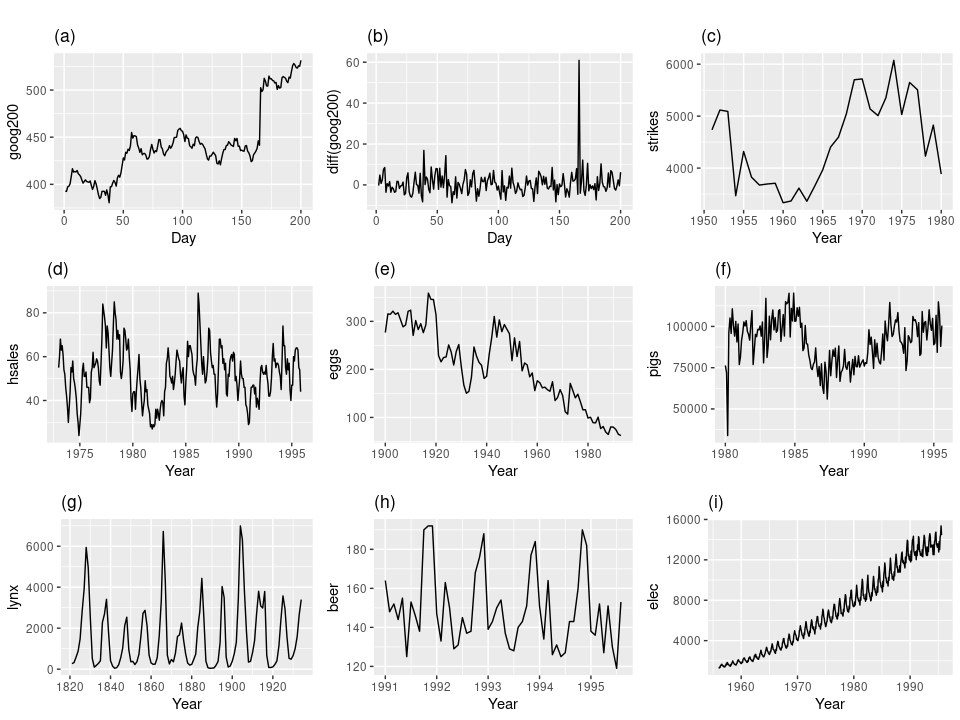
정상성의 정의에 따라
- 그래프에서 추세가 보이면 안됩니다.
- 과거의 변동폭과 현재의 변동폭이 같아야 합니다.
- 계절성이 보이면 안됩니다.
에 해당하는 그래프는 b와 g뿐입니다.
b그래프를 보면 위쪽으로 툭 튀는 부분이 있긴하나 정상성으로 간주할 수 있는 범위입니다. g는 처음에 보면 계절성을 갖고 있는 비정상 그래프인 것처럼 보이나 자세히 보면 주기의 시점이 불규칙하고 확률과정의 분산이 일정하며 추세가 보이지 않기 때문에 정상성 그래프입니다.
ACF, PACF
위처럼 눈으로 확인하는 방법도 있고 자기 상관 함수(ACF; Auto Correlation Function)을 이용하는 방법도 있습니다. 여기서 자기 상관 함수란 현재 시점의 자료와 시점의 차이(Lag)를 가진 자료의 상관성을 나타내는 측도를 말합니다. 편 자기 상관 함수(PACF)는 두 시점 내의 구간 값을 고려하지 않고 두 시점의 상관관계를 확인하는 것입니다. 정상성의 개념을 고려하면서 ACF 그래프를 보았을 때 상관 값이 빠르게 0으로 줄어들면, 즉 전의 값과 연관이 없으면 정상성을 띤다고 볼 수 있습니다.
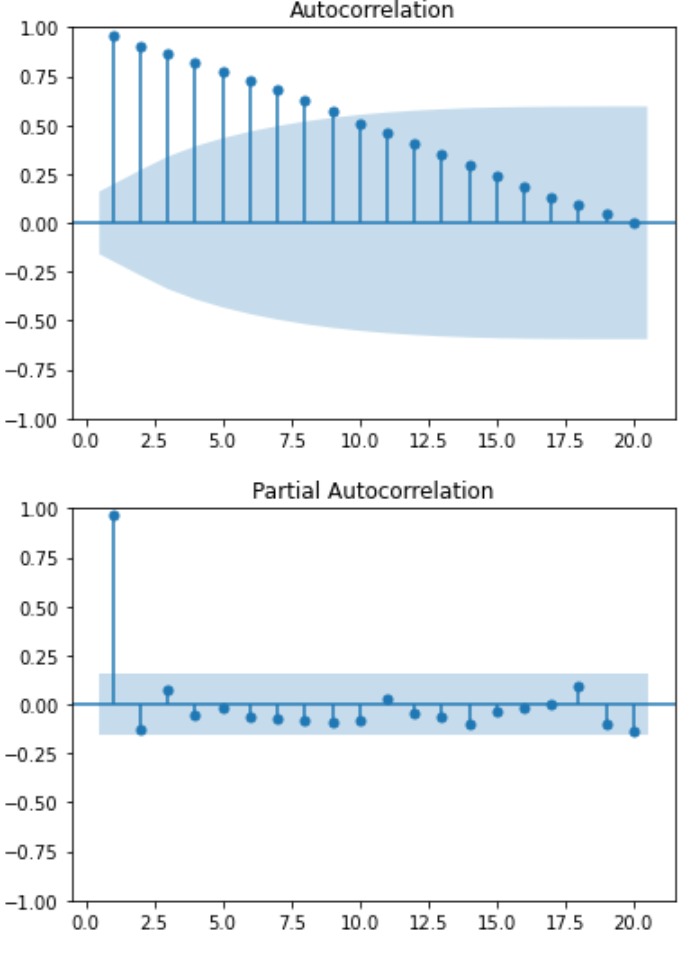
위의 ACF 그래프를 보면 correlation이 내려가는 것을 볼 수 있지만 느리게 감소하며 신뢰구간에는 전혀 들어가지 못하는 모습을 볼 수 있습니다. 고로 비정상적이라고 판단할 수 있습니다. 옆의 PACF 그래프를 보면 시차 1까지 상관이 높은 것을 확인 할 수 있습니다.
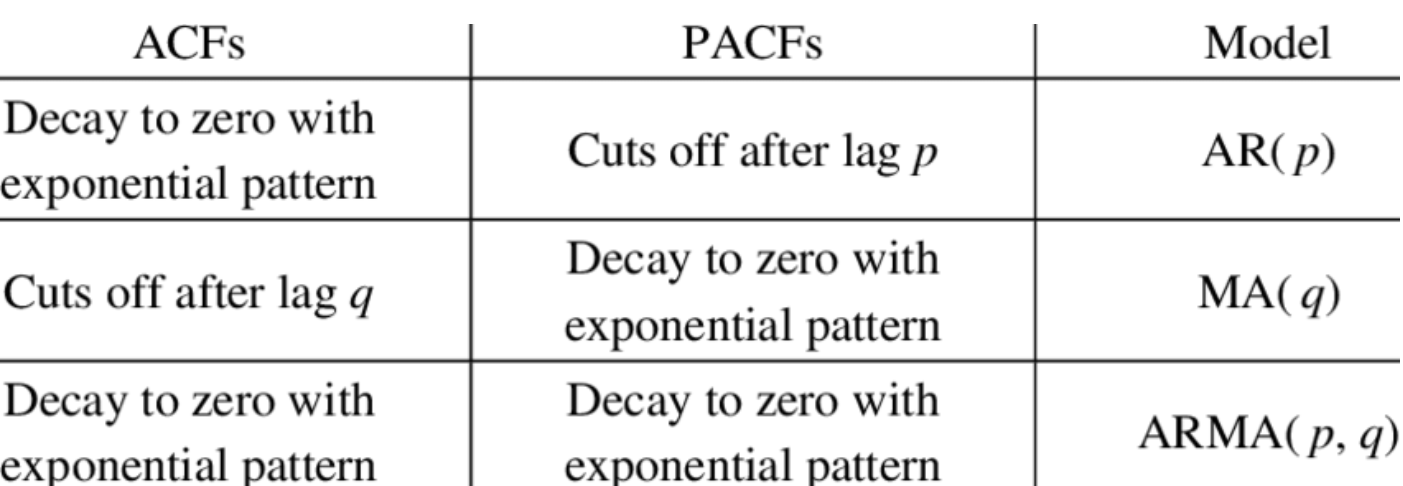
또한 위와 같이 위이 그래프들에서 확인한 값으로 ARIMA 모형을 결정할 수 있습니다. ACF가 감소하고 PACF가 p에서 그래프가 파란색 영역 안으로 들어가면 AR(p) 모형, 반대면 MA(q)모형 마지막으로 둘 다 0으로 가면 ARMA(p, q)를 선택하면 됩니다. 그리고 차분을 결정해주면 되겠죠.
import statsmodels.graphics.tsaplots as sgt
import matplotlib.pyplot as plt
import FinanceDataReader as fdr
import pyupbit
pyupbit.get_current_price(["KRW-BTC", "KRW-XRP"])
a=pyupbit.get_ohlcv("KRW-XRP", to="20210301",interval="day",count=150)
sgt.plot_acf(a['close'], lags = 20, zero = False)
sgt.plot_pacf(a['close'], lags = 20, zero = False)
plt.show()
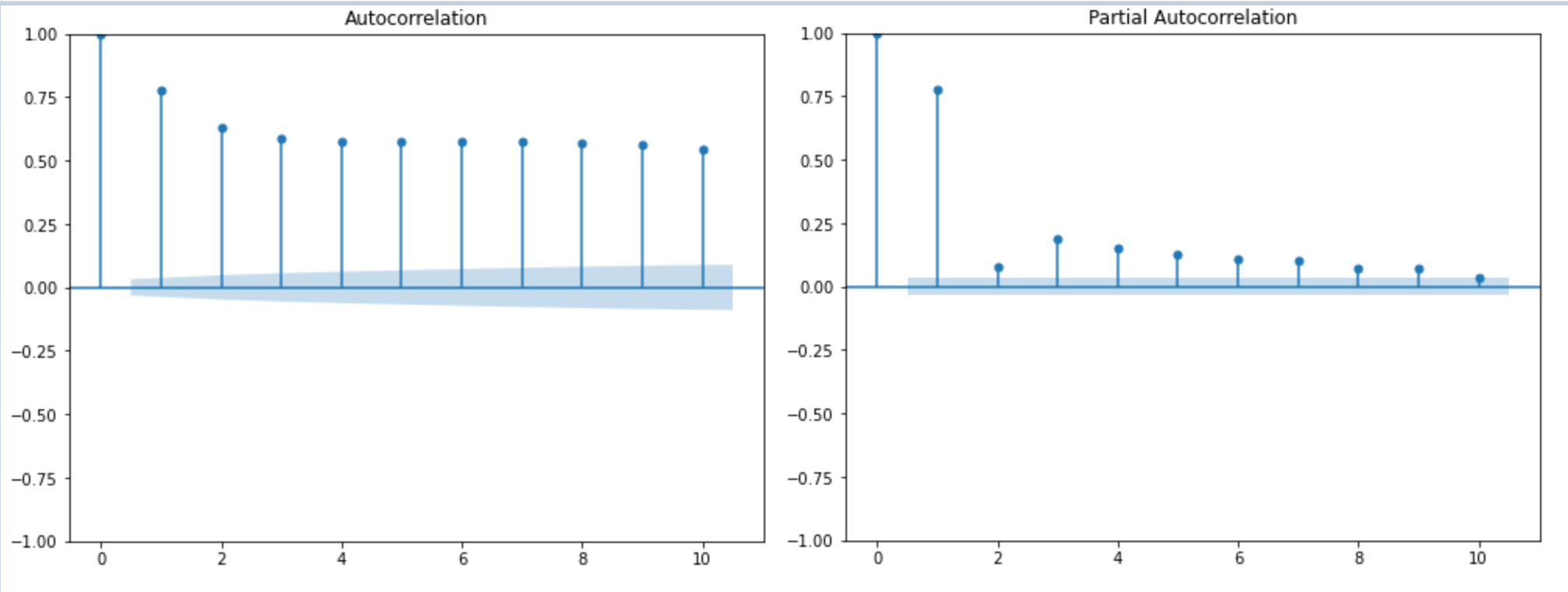
위의 그래프는 upbit 기준으로 2021년 03월 01일부터 150일간의 리플(XRP)의 종가를 ACF로 나타낸 것입니다. ACF를 보면 값이 빠른 속도로 범위 안으로 들어가고 있고 PACF는 1 이후에 범위 안으로 들어간 것을 보면 AR(1) 모델을 활용하는 것이 적합하다고 판단할 수 있습니다.
가설 검정
단측 검정이며 귀무가설은 'H0: 비정상성을 띤다. δ=0'로 p-value가 유의수준 0.05보다 작아 귀무가설을 기각하고 대립가설을 채택해야 정상성을 띠는 것입니다.
단위근 검정
- KPSS 검정
- Dicky-Fuller 검정
- ADF(Augmented Dicky-Fuller Test) 검정
저는 단위근 검정 실습을 할 때 제일 무난한 Dicky_Fuller를 사용하였습니다.
이 방법에는 3가지 종류가 있습니다.
- 상수항, 시간적 추세 둘 다 없는 경우
- 상수항은 있고, 시간적 추세가 없는 경우
- 상수항, 시간적 추세 둘 다 있는 경우
그런데 식만 다를뿐이지 사실상 p-value나 검정통계량 값으로 유의수준 또는 임계치와 비교하여 판단만 내려주면 됩니다. 귀무가설과 대립가설은 위에 써둔 설명과 같습니다.
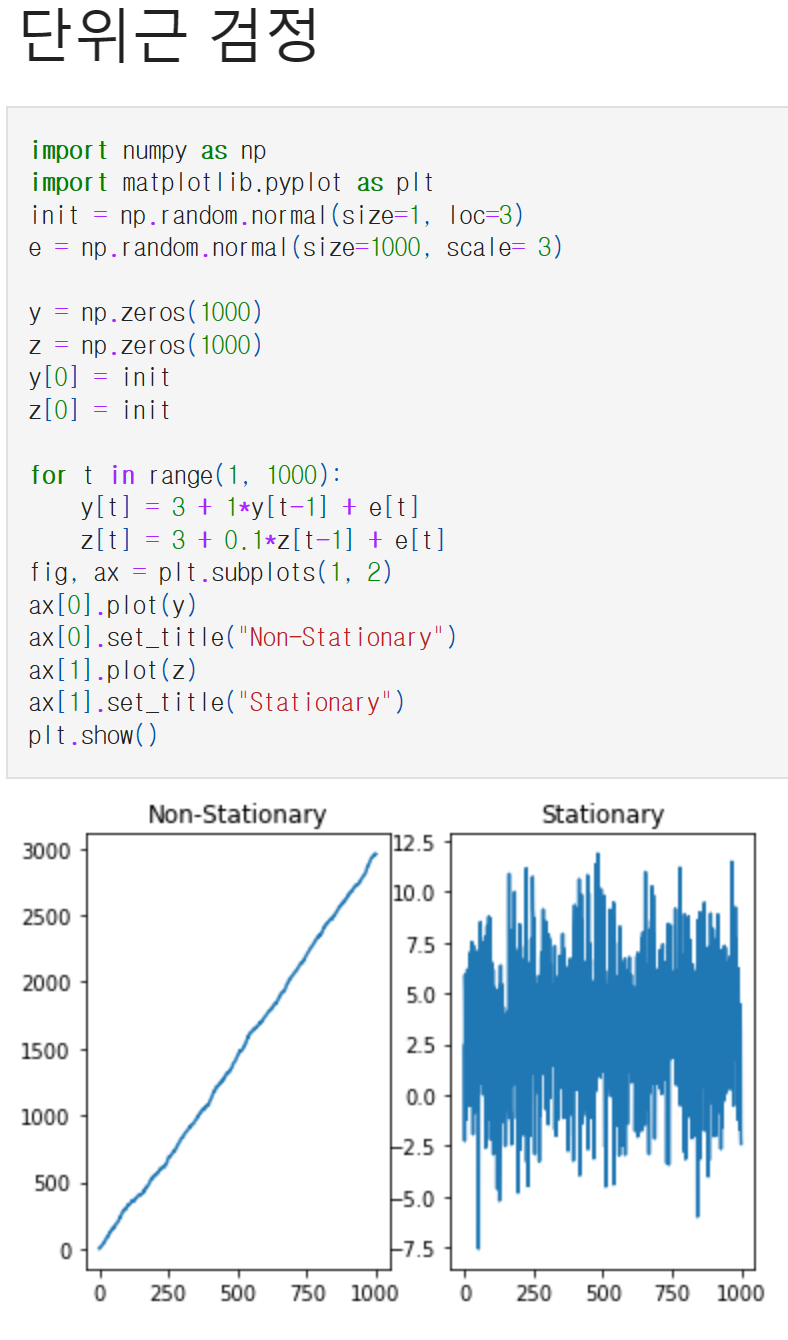
단위근 검정시 계수가 1 즉, 단위근인 경우 왼쪽 그래프처럼 비정상성을 띠고 계수의 절대값이 1보다 작으면 정상성을 띠는 식입니다. 단위근 검정 후 비정상성을 띠면 차분을 고려하면 됩니다.
정상성으로 만드는 방법
1.차분
- 차분은 t시점과 t-1시점의 값의 차이를 구하는 것을 말합니다.
위의 9가지 그래프 중에 a는 구글 주식 가격의 원본 그래프, b는 그것을 차분한 그래프입니다. 이처럼 차분을 하게 되면 값의 차이는 평균이 일정하기 때문에 정상성을 띠게 됩니다.
식은 다음과 같습니다.
Δyt=yt−yt−1
만약 1차 차분을 해도 정상성을 띠지 않는다면 2차 차분을 해주면 됩니다. 그 이상의 차분은 가능하지만 거의 모든 데이터가 2차 차분으로 정상성을 띠기 떄문에 2차 차분이 끝이라고 생각해도 됩니다.
Δyt−Δyt−1=(yt−yt−1)−(yt−1−yt−2)=yt−2yt−1+yt−2 (2차 차분)
위에서 ACF와 PACF를 통해 ARMIA 모형을 정할 때 d의 값이 차분인데 처음에 정상성을 띠지 않는다면 차분을 진행하면서 d의 값을 정해주시면 됩니다.
2.로그 변환
- 로그 변환은 말 그대로 시계열 데이터 값에 로그를 취하는 것입니다. 이를 통해 정상성을 띠지 않는 시계열 자료의 분산을 줄여 정상성을 띠게 만들 수 있습니다.
yt→log(yt)
3.로그 차분
- 이 방식은 로그 변환으로 지수적인 시계열 데이터를 선형적으로 바꿔주고 분산을 안정화 시킨 후 차분을 추가적으로 진행하여 정상성을 띠게하는 방법입니다.
또한 로그 차분 방식은 증가율의 근사값으로 알려져 있고 식과 방법이 쉬운 반면 해석 상 이점이 있습니다.
Δlog(yt)=logyt−logyt−1
리플로 보는 정상성 판단 + 정상성 만들기 코드 github
마무리: 다음시간에는 ARIMA에 대하여 딥하게 다뤄보겠습니다.
reference: https://otexts.com/fpp2/stationarity.html
https://assaeunji.github.io/statistics/2021-08-08-stationarity/
https://direction-f.tistory.com/65