AR(Auto Regressive)

AR모형은 자신의 과거의 관측값을 토대로 미래를 예측하겠다는 의미를 가진 모델입니다.
$y_t = c + \Phi_1y_{t-1} + \Phi_2y_{t-2} + \cdots + \Phi_py_{t-p} + \epsilon_t$
위의 식을 보면 yt, yt-1 이런식으로 주욱 나열되어 있습니다.
여기서 $\epsilon_t$는 백색잡음(white noise)입니다.

MA(Moving Average)

MA모형은 과거의 오차값을 이용해 미래를 예측하는 모델입니다.
$y_t = c + \epsilon_t + \theta_1\epsilon_{t-1} + \theta_2\epsilon_{t-2} + \cdots + \theta_q\epsilon_{t-q}$
MA 모형은 과거의 충격(오차)이 현재의 결과에 영향을 주는 경우에 사용합니다.

ARIMA(AR+Integrated+MA)

ARIMA 모델은 과거의 관측값과 오차를 모두 이용하는 모형입니다.
그래서 AR과 MA는 위에서 언급한 모형과 같은 뜻이고 추가된 I는 차분을 뜻합니다.
$y_t' = c + \Phi_1y_{t-1}' + \cdots + \Phi_py_{t-p}' + \theta_1\epsilon_{t-1} + \cdots + \theta_q\epsilon_{t-p} + \epsilon_t$
여기서 y프라임은 차분한 것을 뜻하고 이는 한 번 이상의 차분일 수도 있습니다.
ARIMA 모형을 만들 때 매개변수 3개를 넣는데 순서대로 p, d, q입니다.
여기서 p는 AR 부분의 차수, d는 차분의 정도, q는 MA부분의 차수를 뜻합니다.

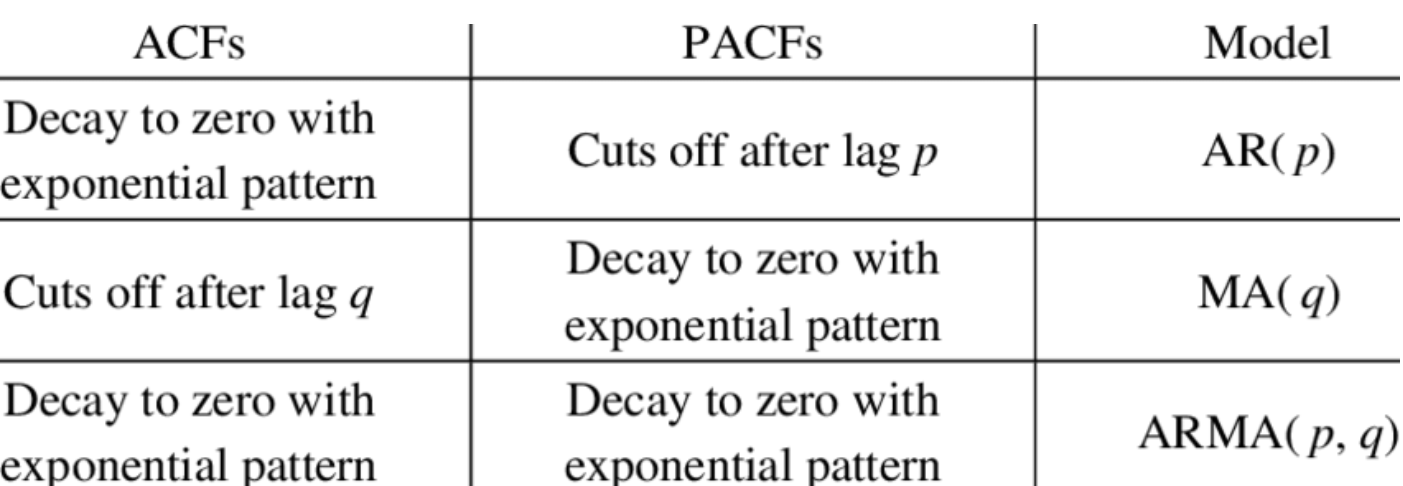
ACF, PACF와 위의 표를 참고하여 p와 q를 정하면 됩니다.

Code

ARIMA로 데이콘 대회(전력사용량 예측) 맛보기

import numpy as np
import pandas as pd
import math
import os
import matplotlib.pyplot as plt
# 넘파이와 판다스, plot은 무조건 필요하고 ARIMA를 써주기 위해서 밑에 언급
from sklearn.metrics import mean_absolute_error #에러 방지용 코드 중요x
from statsmodels.tsa.arima.model import ARIMA

#데이터 불러오기
train = pd.read_csv('eletrain.csv')
test = pd.read_csv('test.csv')
train['비전기냉방설비운영'].fillna(0, inplace=True)
train['태양광보유'].fillna(0, inplace=True)
submission = pd.read_csv('sample_submission_ARIMA.csv')
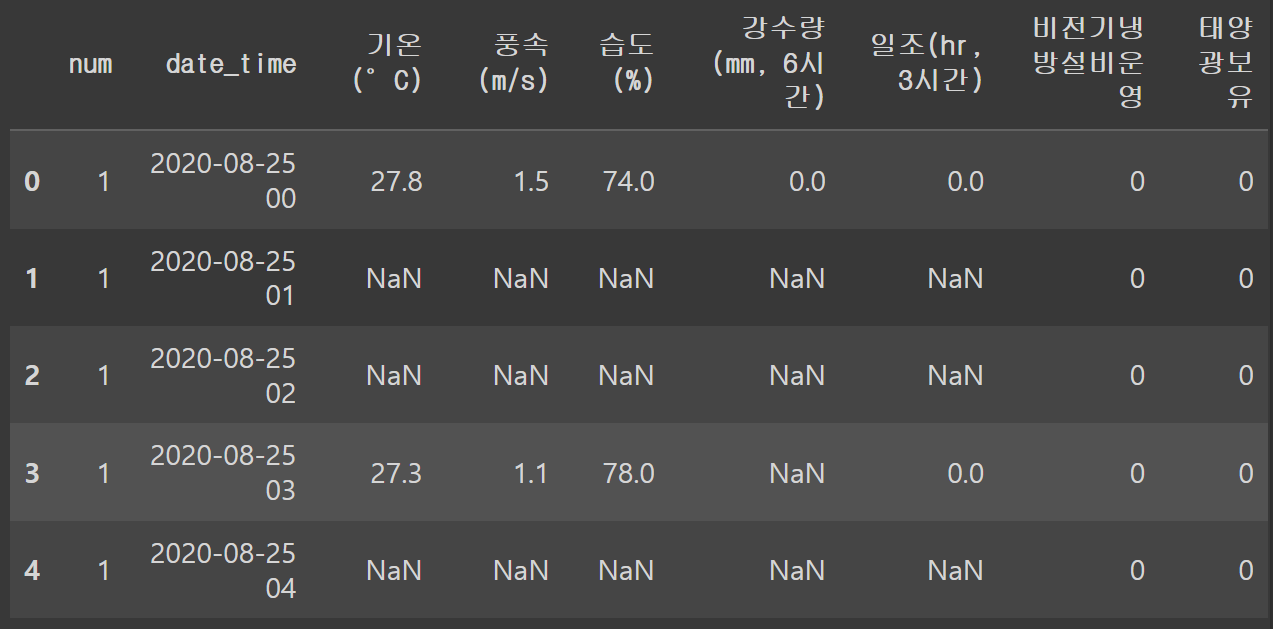
test.head()

위처럼 test.head를 해보면 test에는 3시간마다 값들이 있고 강수량은 6시간마다 값이 있습니다.
다른 방식이었으면 다 전처리 해야하지만 ARIMA는 전력량만, 즉 단변량을 사용하므로 상관X

def df2d_to_array3d(df_2d):
  feature_size = df_2d.iloc[:,2:].shape[1] #특성(전력량, 기온 등)의 개수
  time_size = len(df_2d['date_time'].value_counts()) #시간 개수
  sample_size = len(df_2d.num.value_counts()) #num의 종류? 개수? -> 즉, 건물 몇 개
  return df_2d.iloc[:,2:].values.reshape([sample_size, time_size, feature_size]) # reshape에 인자 넣어주면 알아서 모양 맞춰서 나옴

데이터 프레임을 3d 데이터로 바꿔주는 함수를 정의합니다.

train_x_array = df2d_to_array3d(train)
test_x_array = df2d_to_array3d(test)
print(train_x_array.shape)
print(test_x_array.shape)

결과는
(60, 2040, 8)
(60, 168, 7)

def plot_series(x_series, y_series):
  plt.plot(x_series, label = 'input_series')
  plt.plot(np.arange(len(x_series), len(x_series) + len(y_series)), y_series, label = 'output_series')
  plt.axhline(1, c= 'red')
  plt.legend()

위의 함수는 plot을 그려줄 함수입니다.
여기까지는 데이콘에 있는 베이스라인과 똑같으나 저는 베이스 라인을 믿지 못했고 ACF와 PACF를 그려봤습니다.

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import plotly.graph_objects as go
#아직 시각화 공부가 덜 되어서 이해부탁드립니다. ㅎㅎ
for i in range(60):
  plot_acf(train[train['num']==i+1]['전력사용량(kWh)'])
  plot_pacf(train[train['num']==i+1]['전력사용량(kWh)'])

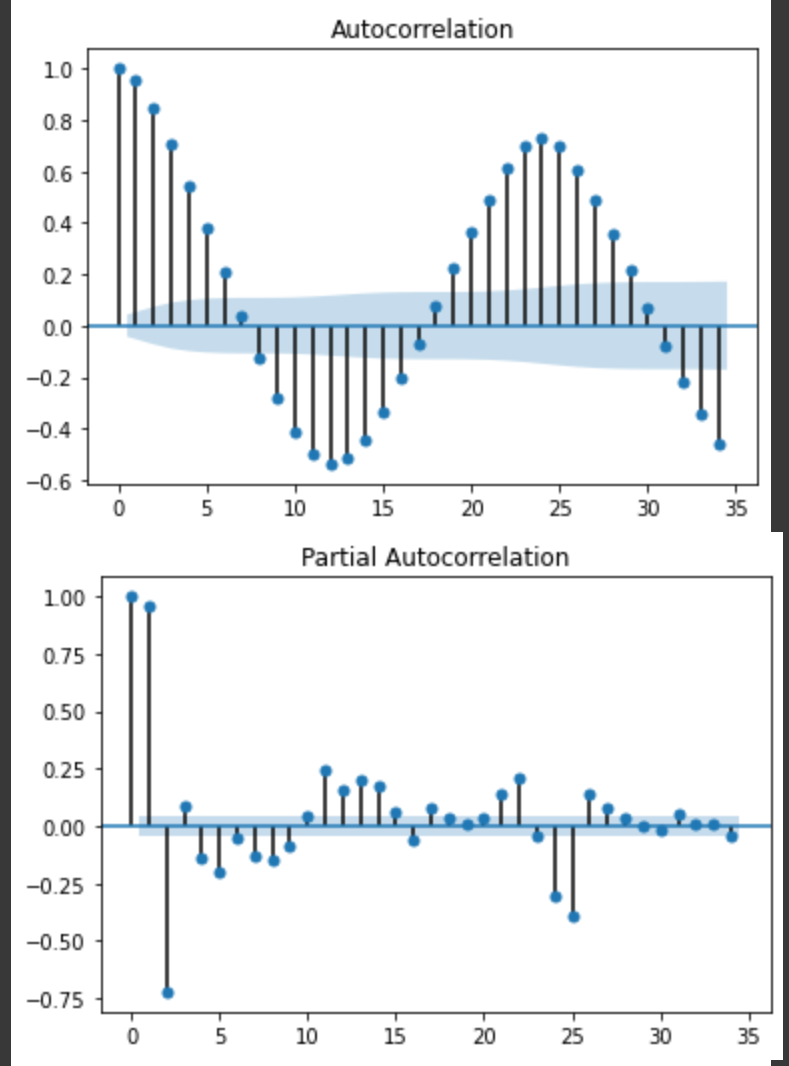
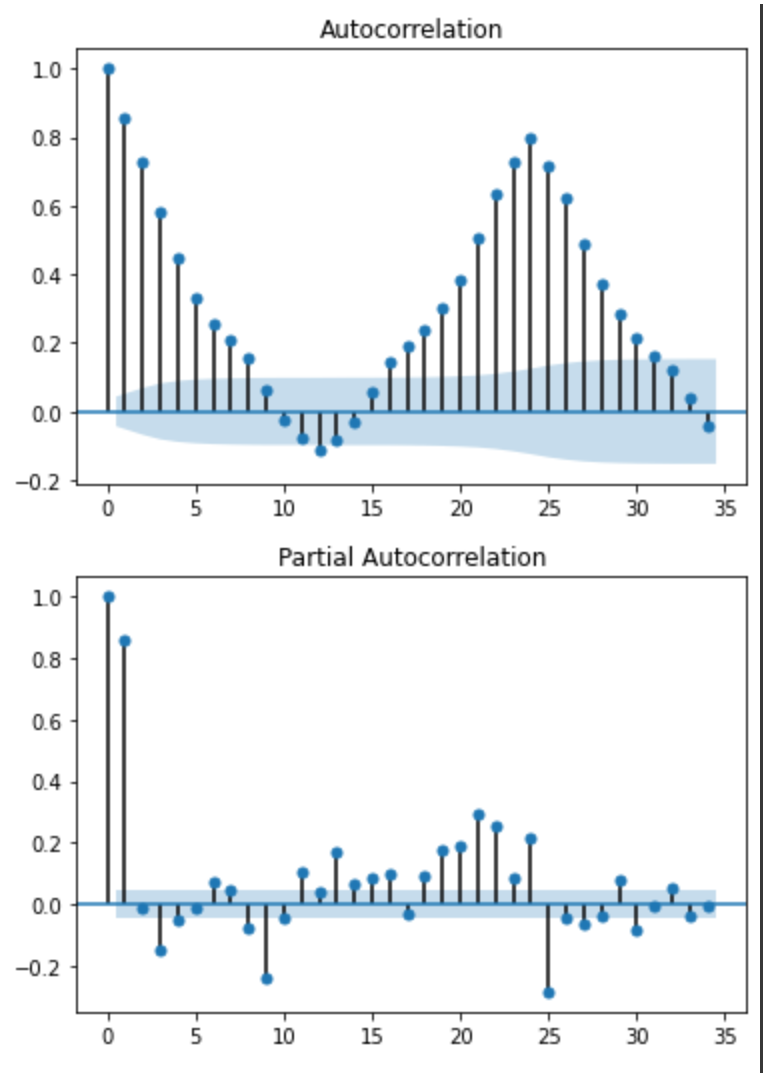
ACF를 보면 6이나 5 다음부터 0으로 수렴하는 경향이 많이 관측되고 PACF는 거의 모든 그래프가 1 다음에는 수렴구간에 들어가기 때문에 p는 6이나 5, q는 1이 적당하다고 판단하였습니다.

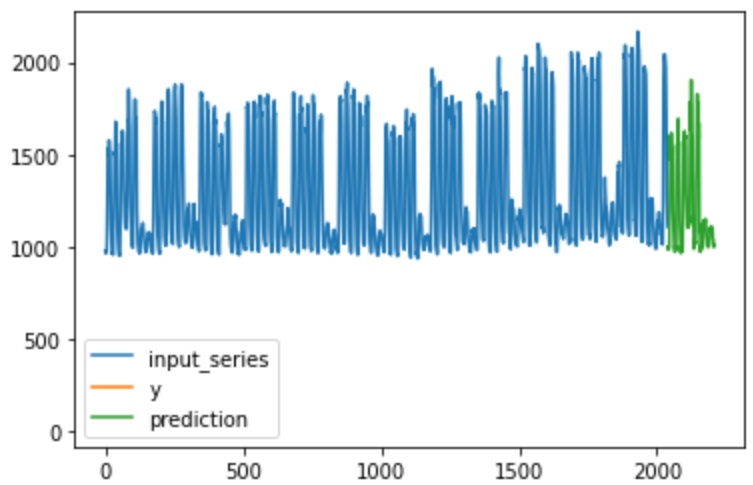
예시로 첫번째 건물을 예측한 그래프를 보겠습니다.

idx = 1
x_series = train_x_array[idx, :, 0]
model = ARIMA(x_series, order = (6, 0 , 1))
fit = model.fit()
preds = fit.predict(1, 168, typ= 'levels')

plt.plot(x_series, label = 'input_series')
plt.plot(np.arange(2040, 2040+168), test_x_array[idx, :, 0], label='y')
plt.plot(np.arange(2040, 2040+168), preds, label='prediction')
plt.legend()

베이스 라인에서는 5 1 1 또는 4 1 1로 적합시켰지만 저는 6 1 1과 5 1 1로 해보겠습니다.
참고로 비정상 시계열이기에 차분을 1회 진행하였습니다.

valid_pred_array=np.zeros([60, 168])
for idx in range(train_x_array.shape[0]):
    try:
        try:
            x_series=train_x_array[idx, :, 0]
            model=ARIMA(x_series, order=(6, 1, 1))
            fit=model.fit()
            preds=fit.predict(1, 168, typ='levels')
            valid_pred_array[idx, :]=preds
        except:
            print("order 5,1,1")
            
            x_series=train_x_array[idx, :, 0]
            model=ARIMA(x_series, order=(5, 1, 1))
            fit=model.fit()
            preds=fit.predict(1, 168, typ='levels')
            valid_pred_array[idx, :]=preds
    except:
        print(idx, "샘플은 수렴하지 않습니다.")

우선 에러는 베이스라인은 7번 제가 시도한 것은 10번으로 베이스라인이 더 적게 떴습니다.

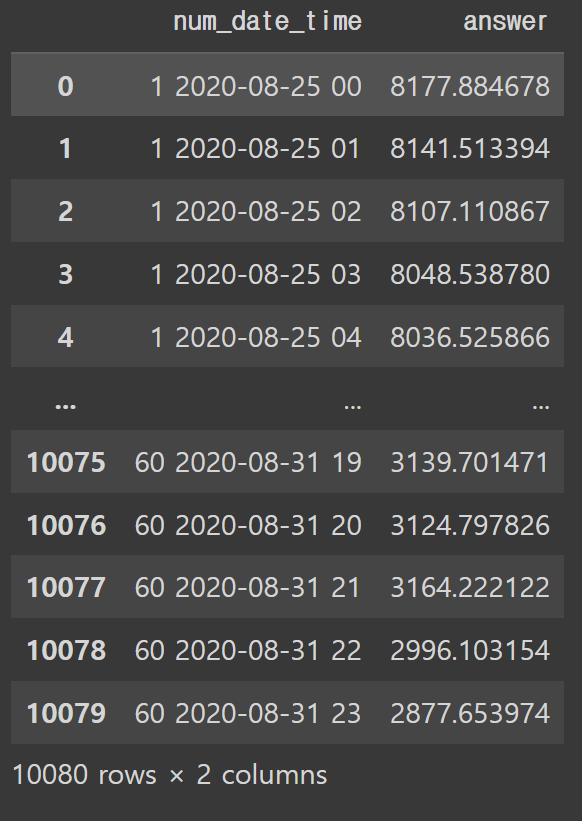
submission['answer']=valid_pred_array.reshape([-1,1])
submission

위는 예측 값입니다.


위의 값은 베이스라인을 그대로 제출하였을 때 나온 손실 점수이고 밑은 제가 수정한 값입니다.
애매하게 걸쳐있는 값들이 많아서 6, 5나 5, 4나 차이가 없는 것 같습니다.

감사합니다.