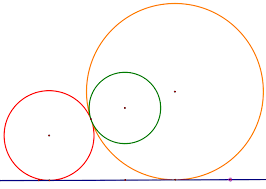
백준 알고리즘 10000번 '원 영역'의 오일러지표를 활용한 풀이입니다. 이론 및 풀이에 대한 조언, 오류 지적 매우 감사합니다!
1. 문제 접근
x 축에 나란하게 여러 원을 놓을때 서로 통과하지는 않지만 서로 접할 수는 있다. 이때 각 원에 의해서 생기는 영역의 갯수를 구하는 문제다.
문제를 처음 보고 사용된 알고리즘에 대한 힌트를 얻을게 없을까 하고 목록을 살피다보니 '오일러 지표' 를 발견했다. 그리고 그게 시작이었다... (마치 밭에서 감자를 하나 뽑았는데 무슨 20개가 딸려오는 느낌)
1.1 오일러 지표란?
수학자 레온하르트 오일러가 발견한 위상수학의 시초격이 되는 식이다.
간략히, 정말 간략히 설명하자면 기하학에서 다면체 혹은 2차원 평면 그래프 등 다양한 도형의 '위상수학적 불변량' 이다. 오늘의 풀이에서 주목할점은 '불변량'이라는 점이다. 원이 몇개가 접하든, 어떻게 접하든 항상 유지되는 점과, 면, 선의 관계가 존재한다는 의미이기 때문이다.
위 식에서 v 는 점의 개수, e 는 선의 개수, f 는 영역의 개수로 인식하면 충분하다 하겠다. (실제 위상수학과는 전혀 다를 수 있음) 이번 문제에 직접 이 식을 적용하게 되면 '2차원 평면 그래프'에 해당하는 식이 된다.
여기서 c 는 컴포넌트 수로 그래프 이론에서 쓰이는 개념중 하나인데, 이 문제에서는 그냥 연결된 원 뭉텅이(?) 로 이해하면 되겠다.
자 그래서 이 식으로 뭘 하면 될까?
문제에서 원하는 답은 나눠지는 영역, 즉 f 값 이다. 그러므로 f 만 남기고 모두 우변으로 이항하면 이렇게 적을 수 있다.
이렇게 되고나면 문제를 해결하기위해 필요한것은 그저 c 값과 v 값 그리고 e 값 뿐이다.
1.2 e(선의 개수) 는 어떻게 구할까?
놀랍게도 가장 간단하다. e = 2 * N 이다. (N 은 문제에서 주어지는 원의 개수) 너무 간단해서 못 믿을 분들을 위해 그림을 첨부한다.
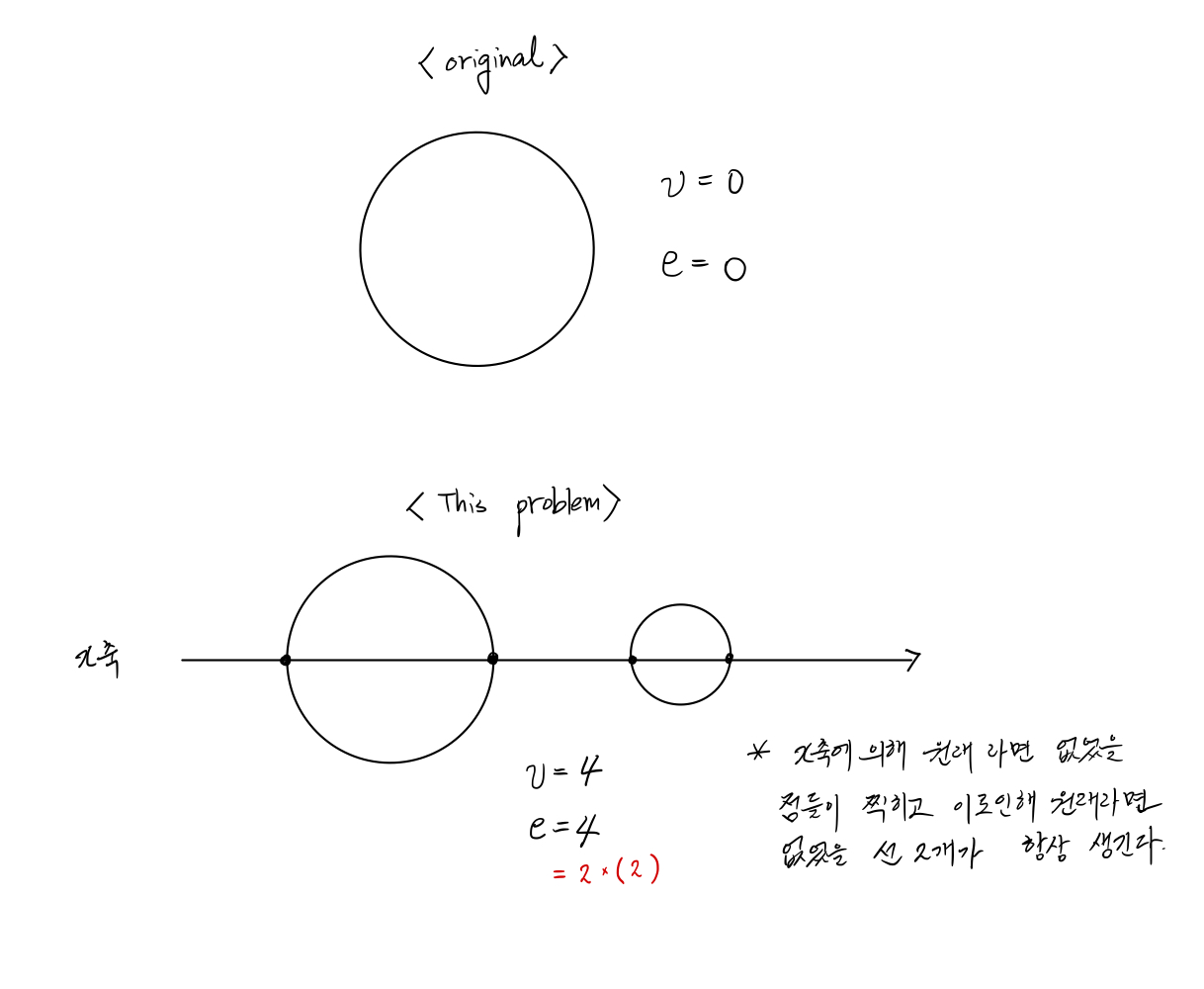
1.3 v(점의 개수)는 어떻게 구할까?
구체적인 설명은 후반부 구현 부분에 가서 코드로 하겠지만 핵심만 전달하자면 주어지는 정보 x(원의 중심 좌표), r(반지름 값) 을 가지고 x-r, x+r 지점의 점을 찍어 배열로 만든다음 중복제거후 정렬을 하게 되면 점의 개수 v 와 일치하는 값이 나온다.
1.4 c(컴포넌트 수)는 어떻게 구할까?
사실상 이 부분 때문에 이 포스트를 쓰게된것이나 다름없다. 다른 고수분들의 알고리즘 풀이를 참고했을때 발견했던건, "유니온 파인드 알고리즘을 사용하면 쉽게 구할 수 있습니다." 였다. 유니온 파인드 알고리즘 이라는 걸 처음본 나로서는 도저히 '쉽게'라는 단어에 공감이 가지않았고 나와같은 생각을 가진 다른이를 위해 지금 글을 적고있다.
2. Union Find Algorithm
유니온 파인드는 트리구조 알고리즘 중 하나로서 특정 노드가 속한 부모 노드를 추적하는 'Find' 와 서로 다른 트리를 합쳐주는 'Union' 으로 이루어져 있다.
2.1 Find
특정 노드, 예를들어 4번 노드를 보면 2번 노드를 가리키고 있고 이는 4번 노드의 부모노드를 의미한다. 그렇게 올라가서 2번 노드의 부모노드를 확인하고 마지막까지 가면 자기 자신을 가리키는 노드가 있는데 거기가 바로 '루트'다.
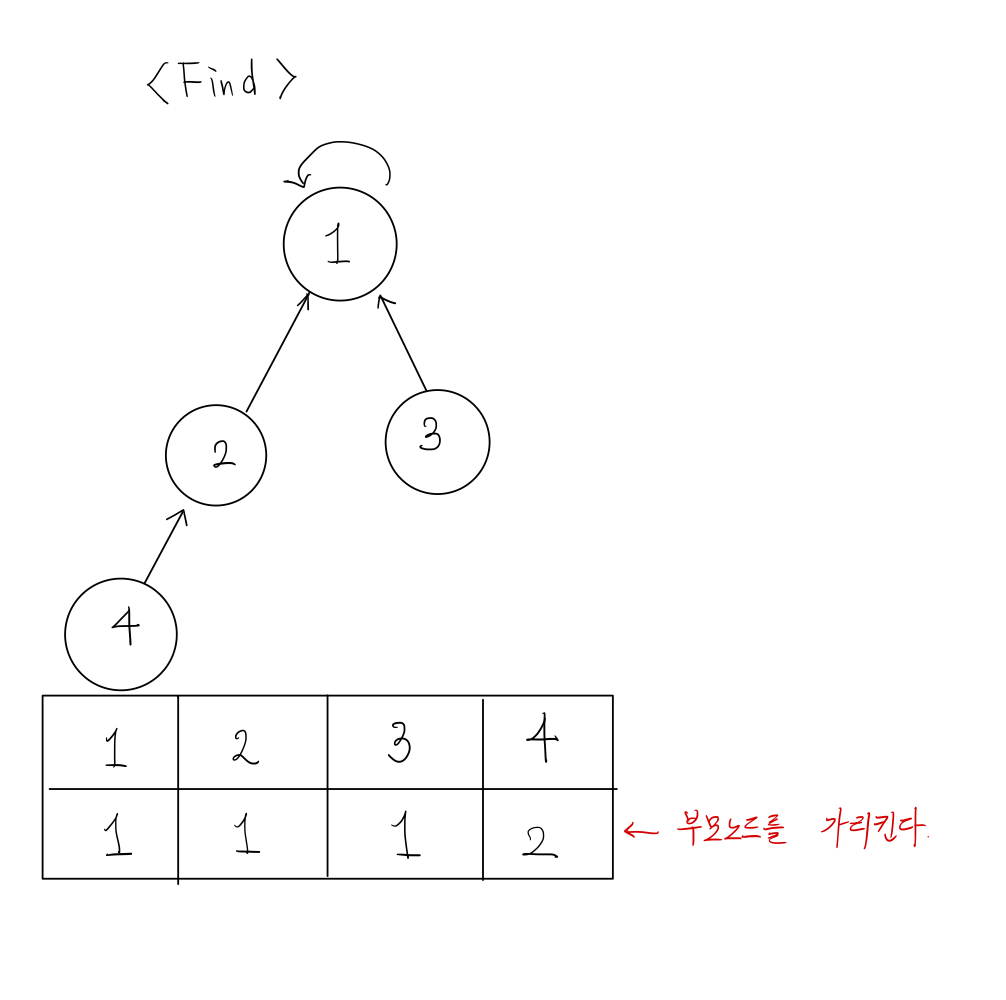
부모를 찾아가는 과정에 재귀를 사용하는데 시간복잡도를 낮추기 위해 경로최적화를 하게된다.
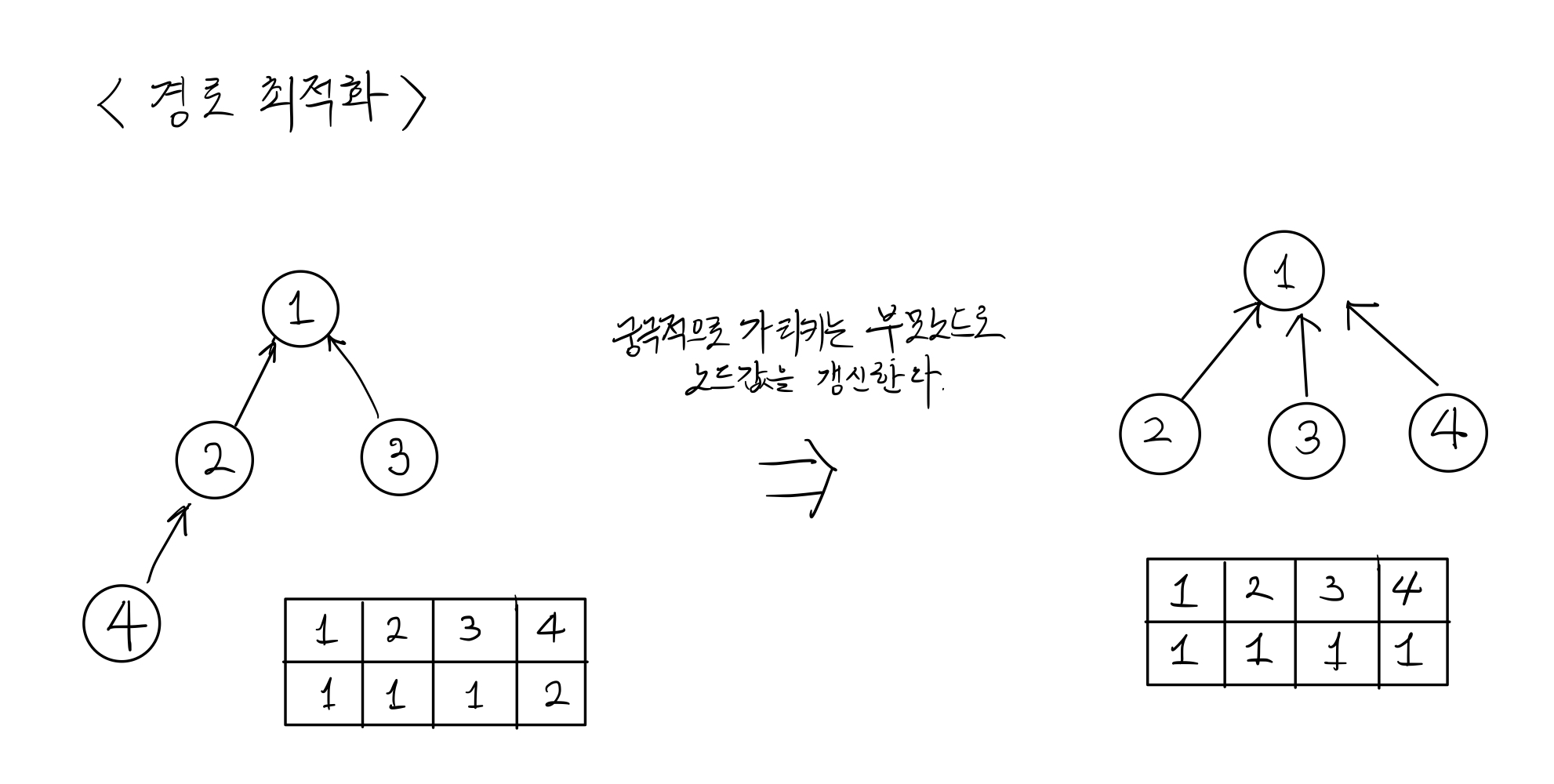
이를 구현한 코드는 다음과 같다.
def find(x):
if parent[x] == x:
return x
# 경로 최적화가 일어나는 부분.
parent[x] = find(parent[x])
return parent[x]즉, 정리하자면 find 부분은 특정노드의 부모 루트가 누구인지를 확인시켜준다. 이 결과를 가지고 Union 부분을 실행한다.
2.2 Union
앞서 실행한 Find 함수의 결과에 따라 부모가 다르다면 두 트리를 합쳐주는데 이때, 트리의 높이가 더 낮은 쪽을 높은 쪽으로 붙인다. 이 과정은 '랭크'를 부여해서 가능하게 하는데 코드를 보면 좀 더 알아보기 쉬울 것이다.
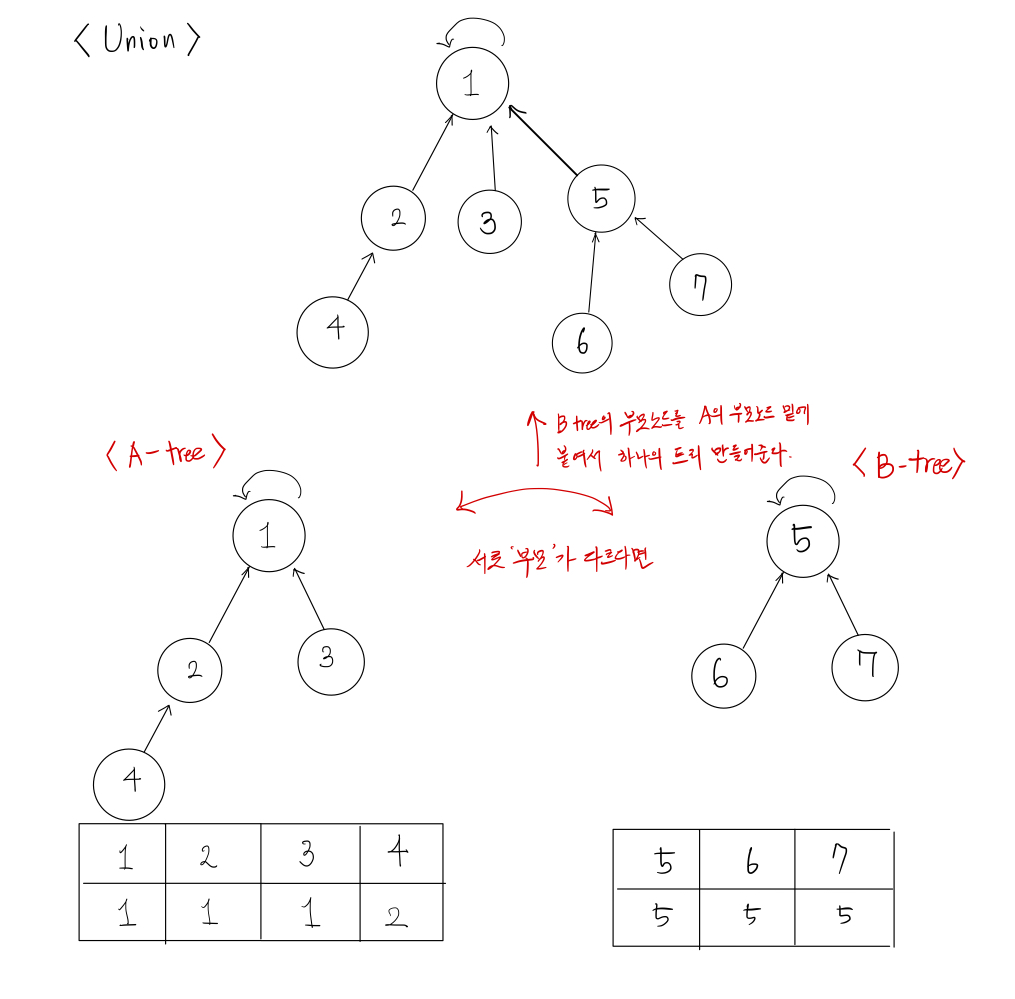
이를 구현하는 코드는 다음과 같다.
def union(x, y):
global cnt
x = find(x)
y = find(y)
# 부모가 같다면 union을 할 수 없다.
if x == y:
return 0
if rank[x] > rank[y]:
parent[y] = x
rank[x] += rank[y]
else:
parent[x] = y
rank[y] += rank[x]
return 12.3 Reset nodes
union find 알고리즘은 최초 노드를 초기화하는 과정이 필요하다. 이는 모든 노드의 부모가 자기자신인 상태로 이 후 최종 구현 코드에서 확인해볼 수 있다.
3. 구현
! 코드 엉성 주의! C++ 로 작성된 코드를 공부하는 과정에서 잘못된 해석이 있을 수 있습니다. 로직에 잘못된 부분이 있다면 언제든 댓글 부탁드립니다.
# 원 영역. 오일러 지표를 사용한 풀이 feat. UnionFind
# 유니온파인드 구현
import bisect
import sys
import itertools
input = sys.stdin.readline
def find(x):
if parent[x] == x:
return x
parent[x] = find(parent[x])
return parent[x]
# 트리를 합치기 전에 랭크를 비교해서 더 짧은 쪽을 더 긴쪽으로 붙인다.
def union(x, y):
global cnt
x = find(x)
y = find(y)
if x == y:
return 0
if rank[x] > rank[y]:
parent[y] = x
rank[x] += rank[y]
else:
parent[x] = y
rank[y] += rank[x]
return 1
N = int(input())
v_list = []
for i in range(N):
x, r = map(int, input().split())
v_list.append([x-r, x+r])
# 2차원 리스트를 1차원으로.
flatten_v = list(itertools.chain.from_iterable(v_list))
comp_v = sorted(list(set(flatten_v)))
L = len(comp_v)
# 2.2.3 초기화 과정. 모든 노드가 자기자신을 부모로 가리킨다.
parent = [0] * L
for i in range(L):
parent[i] = i
rank = [1 for i in range(L+1)]
for i in range(N):
# comp_v 에서 v_stack 의 L[i] 좌표보다 이상의 값이 처음으로 나오는 인덱스 - 처음 인덱스
# 즉 인덱스의 차이를 l 로 선언
l = bisect.bisect_left(comp_v, v_list[i][0])
r = bisect.bisect_left(comp_v, v_list[i][1])
union(l, r)
# 아래 for문에서 컴포넌트 수를 세어준다.
cnt = 0
for i in range(L):
# 부모가 자기자신인 노드의 갯수는 전체 트리의 개수와 일치한다.
if i == find(i):
cnt += 1
e = 2*N
v = L
c = cnt
#오일러 지표 with 2차원 평면 그래프.
f = c - v + e + 1
print(f)
4. 총평
원래 스택으로 원이 열리고 닫히는 지점을 확인해서 푸는 풀이였는데 괜히 '오일러 지표'에 꽂혀서 파고들었다가 union find 알고리즘 까지 공부해버렸다. 심지어 고수 분들은 대부분 C++을 사용하셔서 파이썬밖에 할줄 모르는 나는 C++ 읽는 법 부터 배워야했다.
하지만! 결국에 풀어서 제출했을때의 그 성취감이란...
이 맛에 알고리즘 푸는 건가 보다.

성의글 선댓 후감상