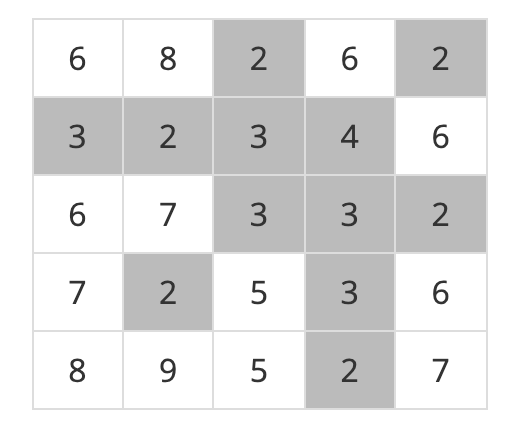
<이와 같이 장마철에 내리는 비의 양에 따라서 물에 잠기지 않는 안전한 영역의 개수는 다르게 된다. 위의 예와 같은 지역에서 내리는 비의 양에 따른 모든 경우를 다 조사해 보면 물에 잠기지 않는 안전한 영역의 개수 중에서 최대인 경우는 5임을 알 수 있다.>
어떤 지역의 높이 정보가 주어졌을 때, 장마철에 물에 잠기지 않는 안전한 영역의 최대 개수를 계산하는 프로그램을 작성하시오.
1. 문제 접근 아이디어
재미있게도 이 문제를 보자마자 떠오른 게임(?)이 있었는데 바로 애플의 "Swift Playground" 였다.

시시각각 변하는 맵의 지형에 맞춰 미리 어떤 상황을 만나면 어떻게 행동할지 프로그래밍을 하는 방식인데, 가령 goForward() 로 앞으로 가다가 벽을 만나면 TurnLeft() TurnLeft() 를 통해 뒤로 돌아 다시 새로운 명령을 수행하는 식이다.
다시 '안전영역' 문제로 돌아와서, 최초로 N X N 크기의 지형정보를 입력받는다. 그리고 비가 내려서 잠기는 영역(지형 높이값이 물 높이 보다 낮은 영역)은 이동할 수 없다. 여기까지 생각해보면 SwiftPlayground의 이동 알고리즘에서 힌트를 얻을 수 있겠다고 생각했다.
2. 알고리즘 설계
2-1. 움직임의 최소단위
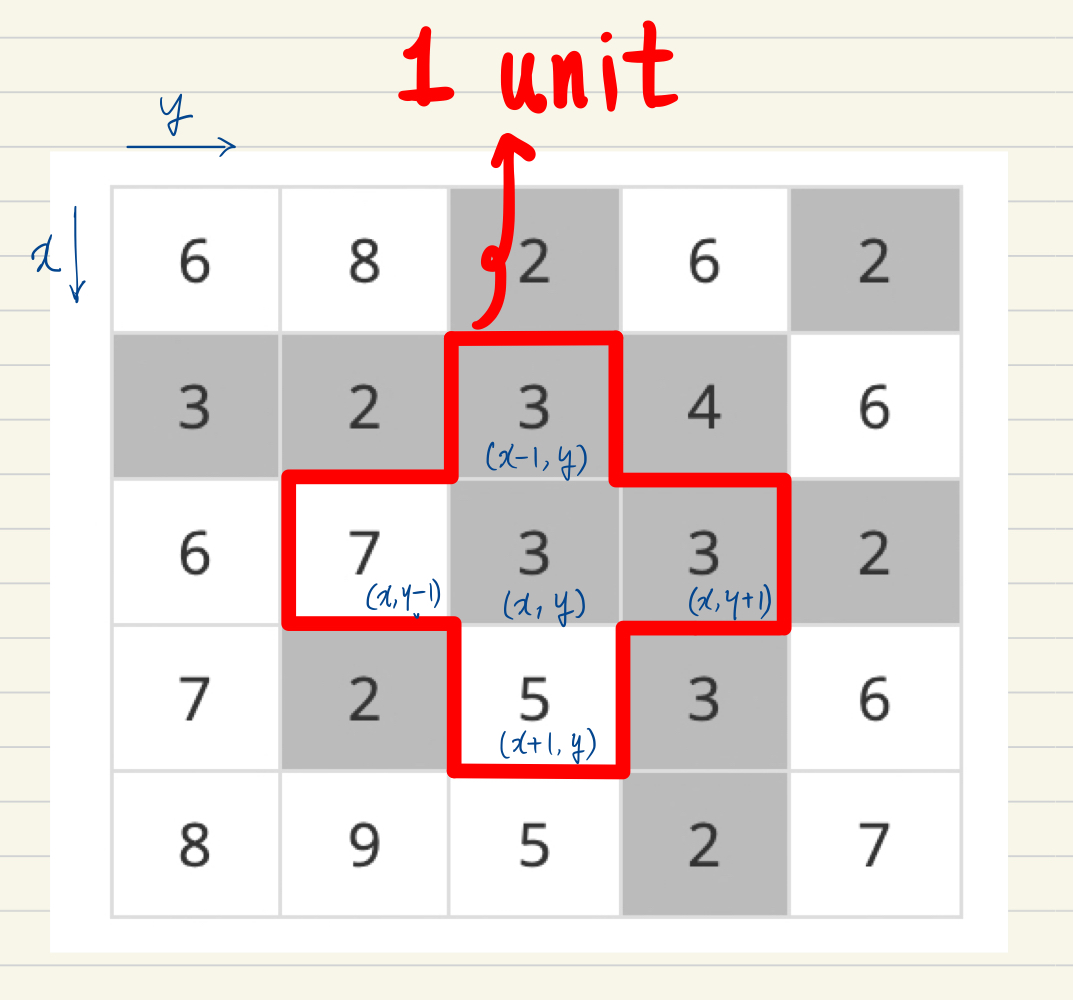
십자 모양으로 영역을 정해서 중앙 좌표를 시작점으로 해서 상 하 좌 우 방향으로 움직인다. 움직임의 최소단위이므로 이후에 함수 단계에서는 재귀의 단위라고 생각해도 될것이다.
2-2. '안전영역'이란 무엇인가?
안전영역이란 움직임의 최소단위로 움직이다가 자기 자신이 온 1칸을 제외한 3면이 막혀있으면 움직임이 끝나고 안전영역이 형성된다.
2-3. 주어진 보드 크기로 어떻게 움직임을 제한할까?
swiftplayground 에서 처럼 '벽을 만나면 뒤로 돈다' 라는 개념을 적용해보았다. '벽을 만나면' => '입력받은 테이블의 인덱스값을 벗어났을때'로 적용해서 움직임(재귀)을 실행하기 전에 필터링 해준다.
2-4. 한쪽 방향으로 뻗어나간 움직임이 막혔더라도 다른 쪽 가지가 막혔는지 어떻게 알고 안전영역의 개수를 증가?
이 부분에서 '재귀 함수'와 'DFS(깊이우선탐색)'의 개념이 사용된다. 이 포스트에서 가볍게 다루고 넘어가기엔 매우 중요한 개념이므로 추후에 다시 다뤄보겠다.
일단 지금은 '한 지점'에서 최초 실행된 재귀함수가 최종적으로 종료될때, 안전영역의 개수를 증가시킨다고 받아들이면 충분해보인다.
2-5. 다음 지점에서 함수가 실행되는 조건은?
'움직임의 최소단위'를 도입했기 때문에 어떻게 움직이게 할 것인가가 중요한 문제중에 하나였다. 이 문제에선 따로 지형 테이블과 동일한 N X N 크기의 'Boolean' 테이블을 설정해서 지형의 지점과 동일한 인덱스를 가지는 boolean 테이블의 True or False 값에 따라 움직임을 결정짓도록 하자.
3. 코드로 구현
3-1. 상 하 좌 우 테크닉.
사실 이부분이 내 기준에선 이 문제의 핵심 아이디어였다. 핵심 아이디어라고 하니 마치 내가 생각해낸것 같지만, 수많은 시간초과를 겪고 난뒤 재귀 깊이를 설정하는 법을 검색한 끝에 다른 고수분들의 코드에서 참조한 것이다. (출처:Dojin Kim 님 github )
#상 하 좌 우 변량
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
#x,y 지점을 기준으로 주변을 탐색하는 재귀함수
def sink_DFS(x, y, h):
# x,y 좌표를 기준으로 상하좌우 좌표를 nx 포문으로 가져옴
for m in range(4):
nx = x + dx[m]
ny = y + dy[m]
# 자신이 건너갈 nx, ny 좌표에 대한 유효성을 먼저 검증함
if (0 <= nx < N) and (0 <= ny < N) and not sink_table[nx][ny] and water_board[nx][ny] > h:이 방법을 통해 움직이기 전에(재귀 함수 호출 전에) 미리 건너갈 좌표에 대한 유효성을 따질 수 있어서 재귀의 깊이를 매우 매우 많이 줄여준다.
3-2. 사용한 재귀함수
#x,y 지점을 기준으로 주변을 탐색하는 재귀함수
def sink_DFS(x, y, h):
# x,y 좌표를 기준으로 상하좌우 좌표를 nx 포문으로 가져옴
for m in range(4):
nx = x + dx[m]
ny = y + dy[m]
# 자신이 건너갈 nx, ny 좌표에 대한 유효성을 먼저 검증함
if (0 <= nx < N) and (0 <= ny < N) and not sink_table[nx][ny] and water_board[nx][ny] > h:
#유효성이 검증된 좌표에 한해서 재귀함수를 호출. 이 과정이 없으면 쌓는 스택이
sink_table[nx][ny] = True
#실질적으로 재귀함수가 하는 역할은 sink_table에 boolean 값만 바꾸는 역할.
sink_DFS(nx, ny, h)
코드를 입력하세요알고리즘 단계에서 따로 언급하지는 않았지만 함수의 변수에 들어있는 h는 물의 높이다. 문제의 조건이 물 높이가 0~100까지 변할때 얻어지는 안전영역 개수의 최대값이기 때문에 마지막에 물높이와 관련된 for문을 통해 최종 답을 구해야한다.
3-4. 최종 코드
위 과정을 거쳐 최종 코드는 다음과 같다.
import sys
sys.setrecursionlimit(100000)
#상 하 좌 우 변량
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
#x,y 지점을 기준으로 주변을 탐색하는 재귀함수
def sink_DFS(x, y, h):
# x,y 좌표를 기준으로 상하좌우 좌표를 nx 포문으로 가져옴
for m in range(4):
nx = x + dx[m]
ny = y + dy[m]
# 자신이 건너갈 nx, ny 좌표에 대한 유효성을 먼저 검증함
if (0 <= nx < N) and (0 <= ny < N) and not sink_table[nx][ny] and water_board[nx][ny] > h:
#유효성이 검증된 좌표에 한해서 재귀함수를 호출. 이 과정이 없으면 쌓는 스택이
sink_table[nx][ny] = True
#실질적으로 재귀함수가 하는 역할은 sink_table에 boolean 값만 바꾸는 역할.
sink_DFS(nx, ny, h)
N = int(sys.stdin.readline())
water_board = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]
#입력값에 따른 물 높이 board 생성
#물에 잠김 여부를 확인할 수 있는 Boolean Table 생성.
# sink_table = [[False for i in range(N)] for j in range(N)]
ans = 1
for k in range(max(map(max, water_board))):
sink_table = [[False]*N for _ in range(N)]
count = 0
for i in range(N):
for j in range(N):
if water_board[i][j] > k and not sink_table[i][j]:
count += 1
sink_table[i][j] = True
sink_DFS(i, j, k)
ans = max(ans, count)
print(ans)p.s. "sys.setrecursionlimit(100000)"은 파이썬을 사용해서 코딩할 시 최대 재귀 깊이를 인위로 늘려줘야했기 때문이다. 안그러면 파이썬은 exceed recursion limit 오류를 돌려준다.
