Hyperparameter Tuning, Batch Normalization and Programming Frameworks

Hyperparameter Tuning

Tuning Process

• 지금까지 우리가 살펴본 다양한 optimization 기법들의 hyperparemeters는 다음과 같다.

  • Learning rate, Momentum & Adam optimizer에 쓰이는 beta, mini-batch size 등 다양한 paremeters를 tuning해야 한다.

• Hyperparemeter 1, 2를 결정하는 방법으로는 random values를 활용하는 방법이 있다.

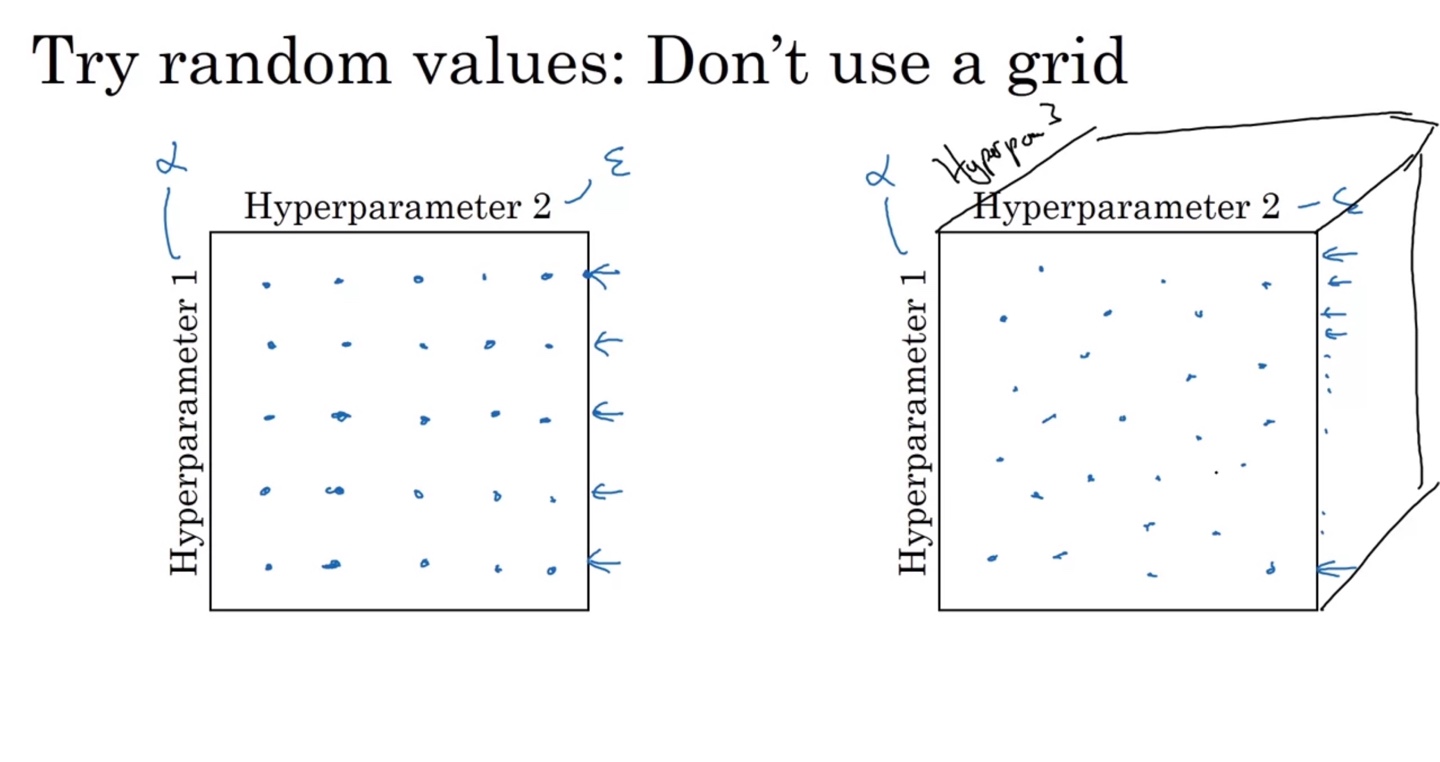
  • 그러나 grid 격자 내의 규칙적인 values는 선택하지 않는 편이 좋다.

    • 왼쪽 그림이 grid 방식, 오른쪽 그림이 random select 방식이다.

    • 오른쪽과 같은 방식으로 선택할 때 더욱 다양한 hyperparemeter 조합을 촘촘히 선택할 수 있기 때문이다.

• 따라서 Random values를 선택하는 것이 Coarse to fine, hyperparemeter의 최적의 조합을 찾는 일이다.

  Coarse to fine은 deep learning 최적화를 위한 세밀한 hyperparemeter 선택 방식을 말한다.

Using an Appropriate Scale to pick Hyperparameters

• Hyperparameter를 random하게 선택하는 방법 중에 효과적인 방법이 있다.

  • Layer가 2-4개라면 tuning하기에 어렵지 않겠지만 50-100개 이상 넘어간다면 선택해야 할 random values가 많아진다.

• 만일 $\alpha$가 0.0001~1 사이의 값이라면 log를 취해 선형적으로 random하게 선택할 수 있다.

  • 그러면 $r$을 -4에서 0 사이의 값과 random.rand()를 곱한 값으로 설정하고, $\alpha$를 $10^r$로 설정하면 hyperparameter의 scale을 조정할 수 있다.

• Adam optimizer에서 사용하는 $\beta$ 값은 보통 0.9에서 0.999 사이의 값으로 결정한다.

  • 0.9는 10 days 전을, 0.999는 1000 days 전을 참조하는 값이다.

    • $1-\beta$로 환산하면 0.1에서 0.0001 사이의 값을 선택하는 것과 같다.

  • 이후 마찬가지로 log scale 조정하여 [-3, -1] 사이의 값으로 random하게 선택하도록 만들면 더욱 효율적인 hyperparameter 선택 방법이 될 수 있다.

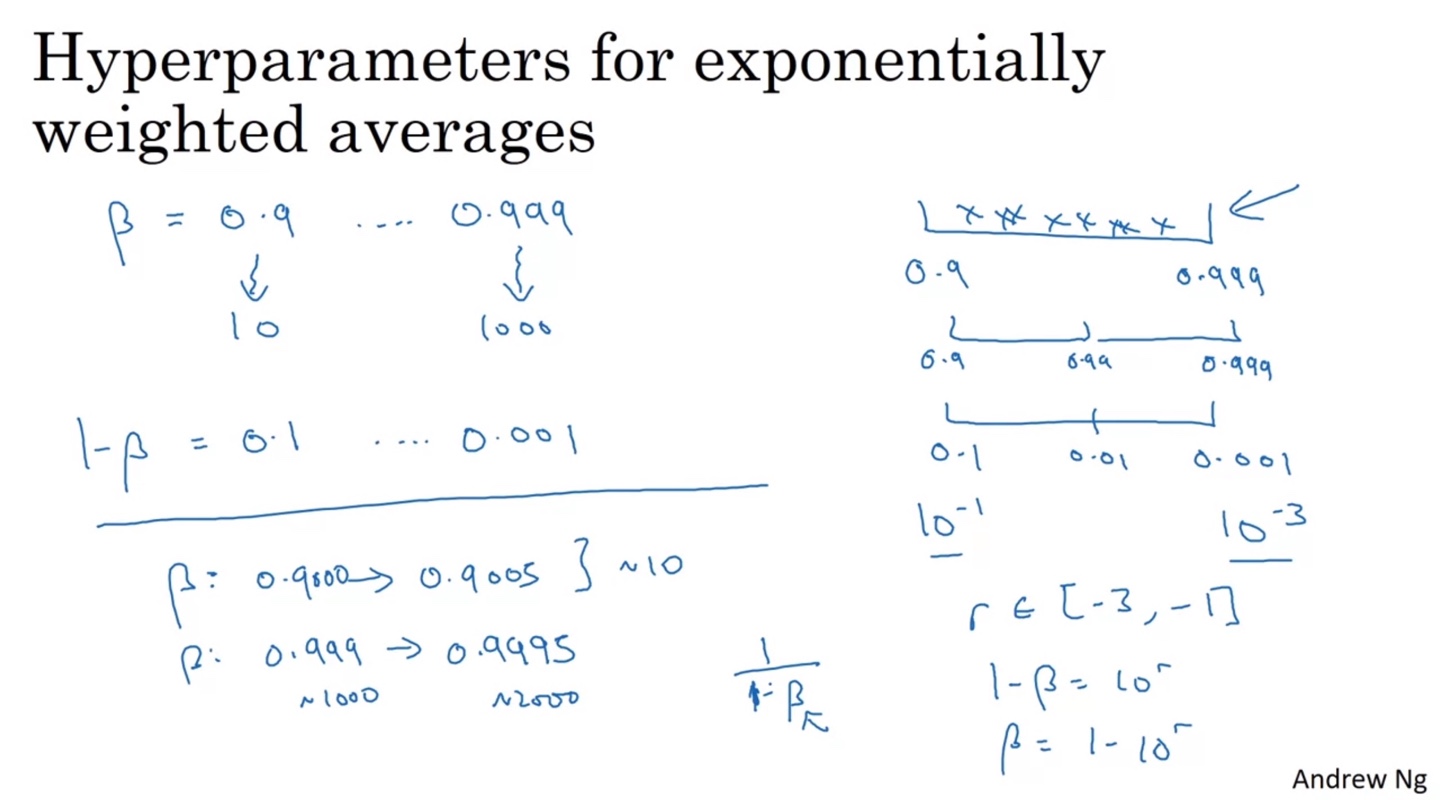
Hyperparameters Tuning in Practice: Pandas vs. Caviar

• Hyperparemaeter를 tuning하는 process는 다음과 같이 지속적이고 신속하게 이루어져야 한다.

  • NLP, Vision, Speech, logistics 등 다양한 도메인에서 요구하는 tuning process에 맞게 re-evaluate하는 과정 또한 직관적으로 알게 되면 좋다.

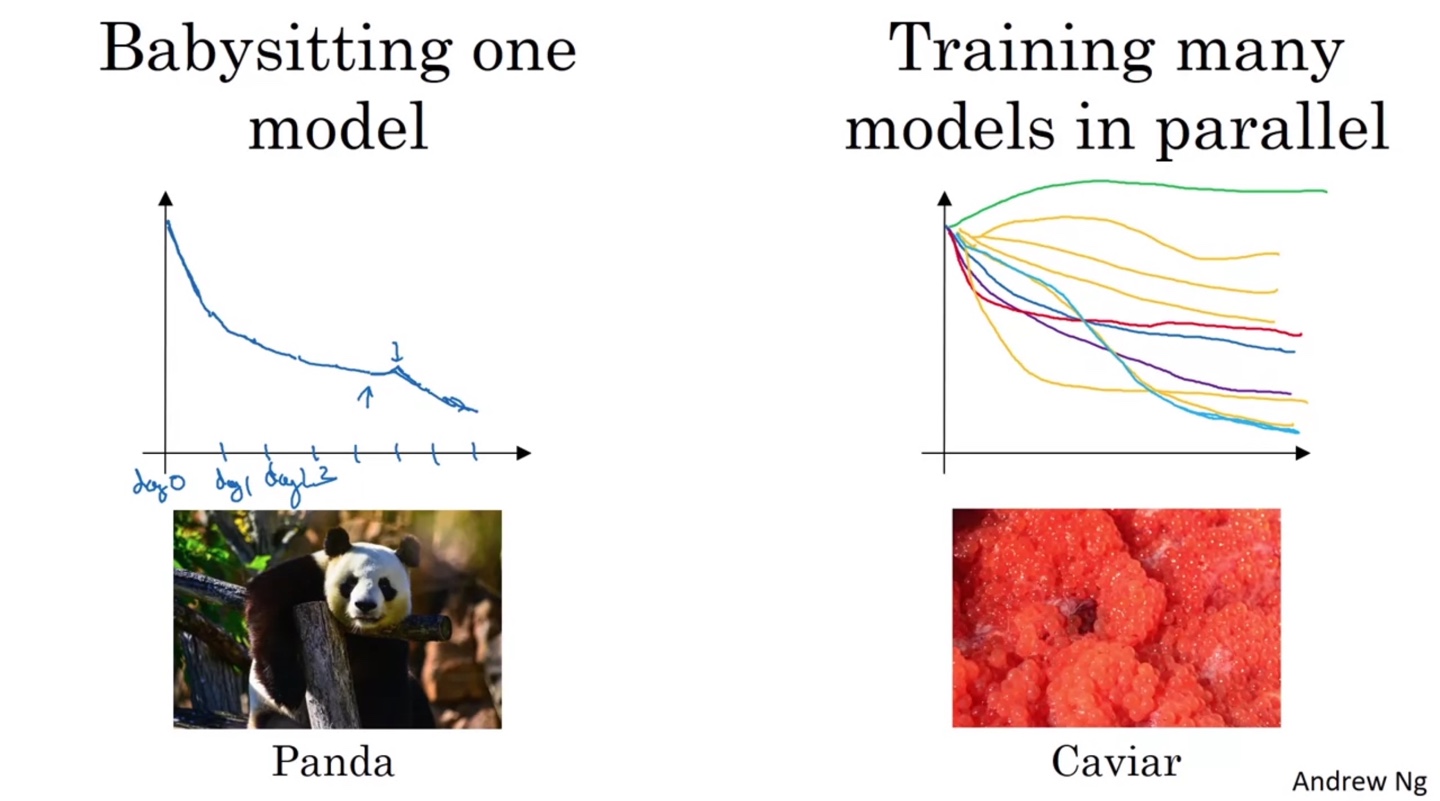
• Hyperparameter tuning process는 다음과 같이 두 가지 방법으로 나눌 수 있다.

  1. 한 모델을 Panda가 babysitting하듯 섬세하게 돌보는 방식
  2. Caviar 알을 낳듯 여러 모델을 병렬적으로 실험해보는 방식

Batch Normalization

Normalizing Activations in a Network

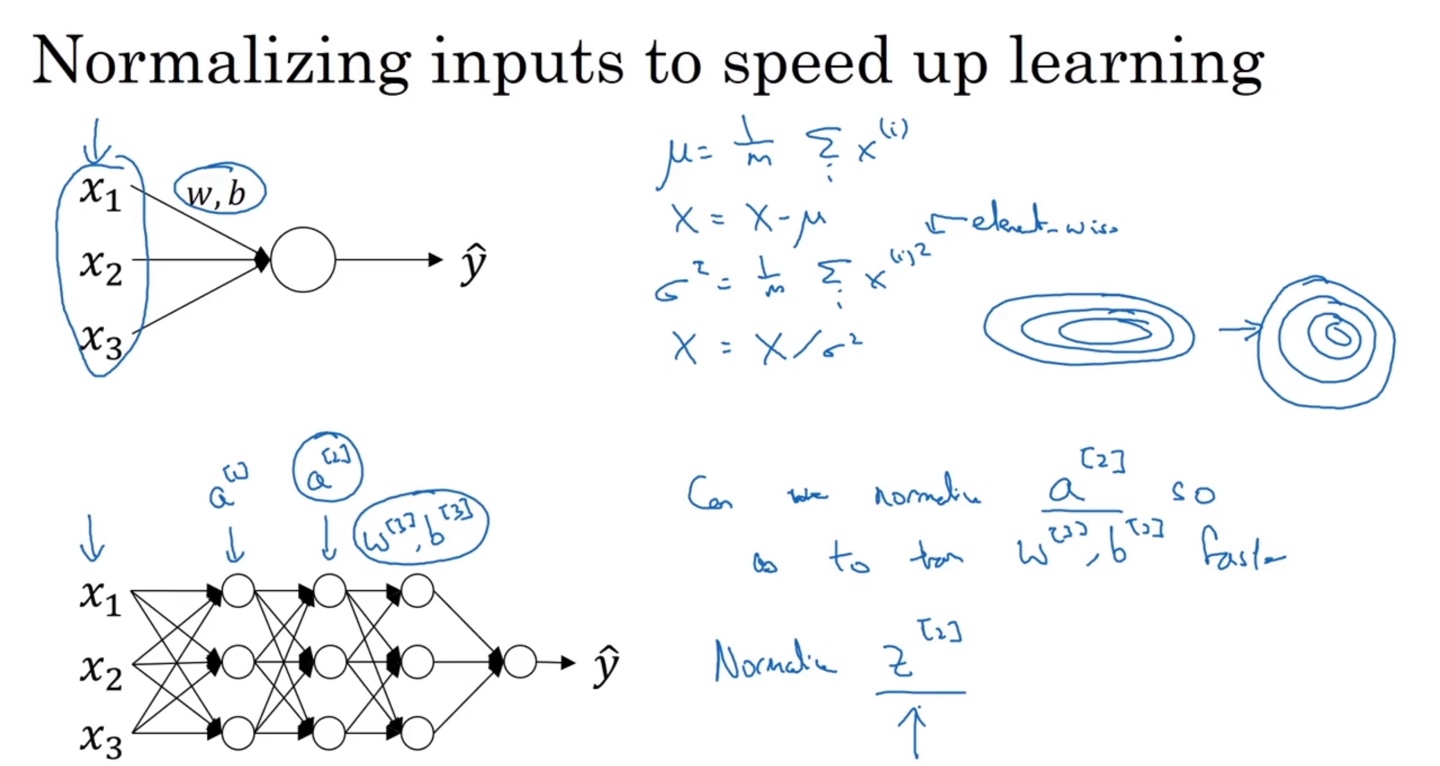
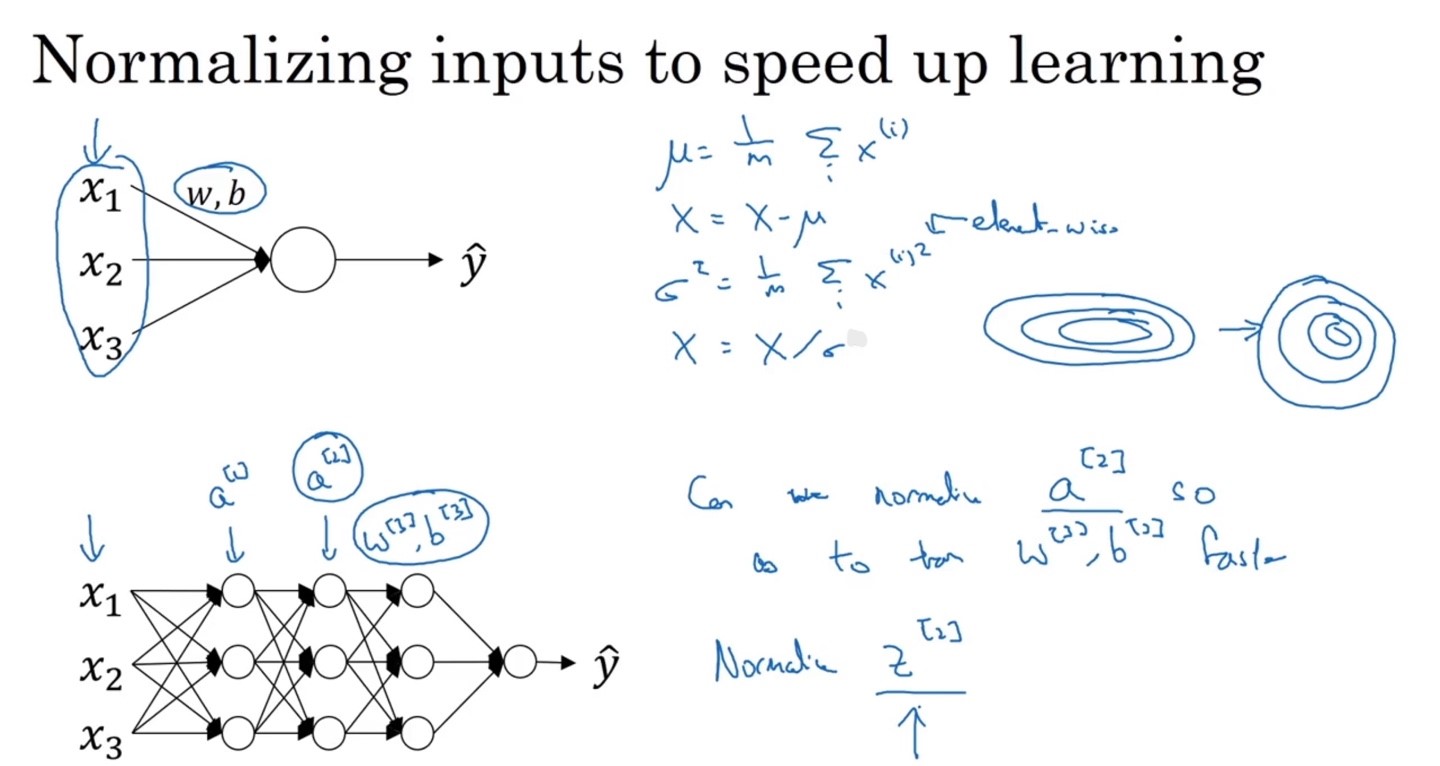
• 앞서 input 데이터를 normalizing하는 이유는 data의 분포를 균등하게 만들 수 있기 때문이라 했다.

  • 그렇다면 deep neural network에서 다음 층의 입력인 $a^{[2]}$를 normalizing한다면 $w^{[3]}$과 $b^{[3]}$의 train을 더욱 faster하게 만들 수 있지 않을까?

    • 이러한 관점에서 batch normalization 개념이 출발하였다.
    • 우리는 $a^{[2]}$가 아닌 $z^{[2]}$를 normailize할 것이다.

• 신경망의 중간값인 $z^{(1)}$부터 $z^{(m)}$까지의 값들을 normalizing하기 위한 일련의 과정은 다음과 같이 이뤄진다.

  • $z^{(i)}$의 평균 $\mu$를 구하고 분산($\sigma^2$)과 표준 편차($\sigma$)로부터 $z_{norm}^{(i)}$을 계산한다.

    • 이 때 ZeroDivision을 막기 위한 $\epsilon$과 추가적으로 tuning할 수 있는 learnable parameter $\gamma$, $\beta$를 곱하여 $\tilde{z}_{norm}^{(i)}$로 대체한다.

    • 만약 $\gamma = \sqrt{\sigma^2 + \epsilon}$과 $\beta = \mu$라면 $\tilde{z}_{norm}^{(i)}$는 $z_{norm}^{(i)}$와 같을 것이다.

  • 이렇게 데이터를 평균이 0인 normalizing 분포를 만들고 나면 activation인 sigmoid를 통과할 때, gradient 값이 dynamic해지기 때문에 효과적이라 할 수 있다.

Fitting Batch Norm into a Neural Network

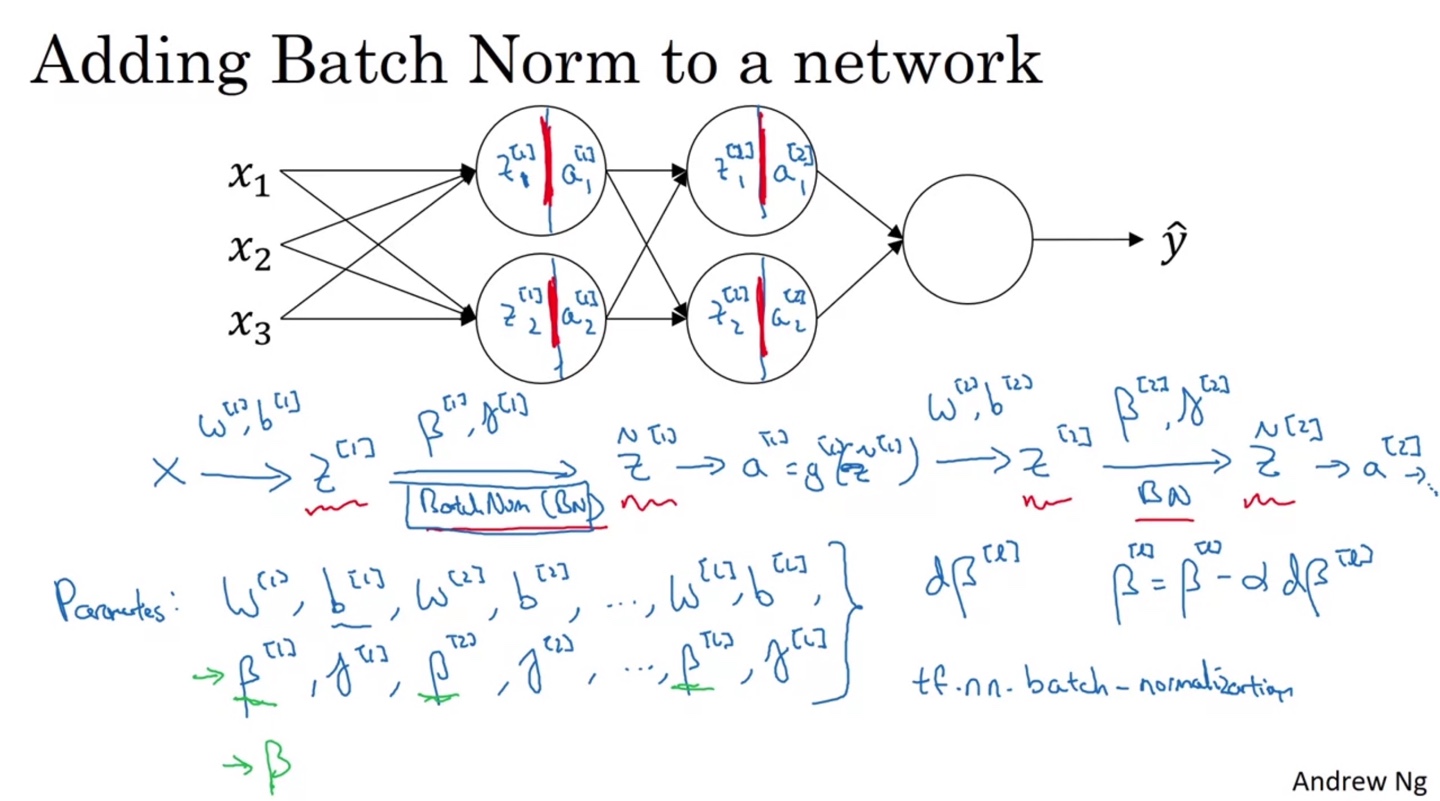
• Neural Network에 Batch Norm을 적용하는 방법은 다음과 같다.

  • $w$와 $b$로 선형 변환(linear transform)된 $z$에 $\beta$와 $\gamma$를 곱한다.

    • 각 layer마다 적용하며 tf.nn.batch_normalization() 함수로 적용할 수 있다.

• 실제 traning은 $t$개의 mini-batches를 iterate하며, 각 mini-batch마다 계산되는 $z$에 batch norm을 적용하는 과정으로 이루어진다.

  • 이 때, 선형적으로 더해지는 $b$는 batch norm에서의 $\beta$와 중복되므로 생략한다.

• Gradient descent는 다음과 같이 이루어진다.

  • $m$개의 mini-batches를 iterate하며 $X^{\{t\}}$를 forward prop한다.

    • Batch Norm을 적용한 $z^{[l]}$ 대신 $\tilde{z}^{[l]}$를 계산하고, $b$를 제외한 $W$, $\beta$, $\gamma$ parameters를 back prop한 후 update한다.

  • Optimization은 Momentum이나 Adam 알고리즘으로 작동하게 한다.

Why does Batch Norm work?

• Batch Norm이 왜 필요한지에 대해 알아보기 위해서는 "Covariate Shift"라는 개념에 대해 정의할 필요가 있다.

  • 만약 고양이와 강아지를 classification하는 task에서 검은 고양이만 training set에 포함되었다고 가정해보자.

    • 이후 다양한 색깔의 고양이 사진이 들어온다면 같은 라벨임에도 input data의 distribution이 바뀌어버리는 현상이 나타날 것이다.

  • 따라서 이를 올바르게 구별할 수 있는 견고(robust)한 boundary를 갖는 모델을 만들기 위해 batch normalization이 필요하다!

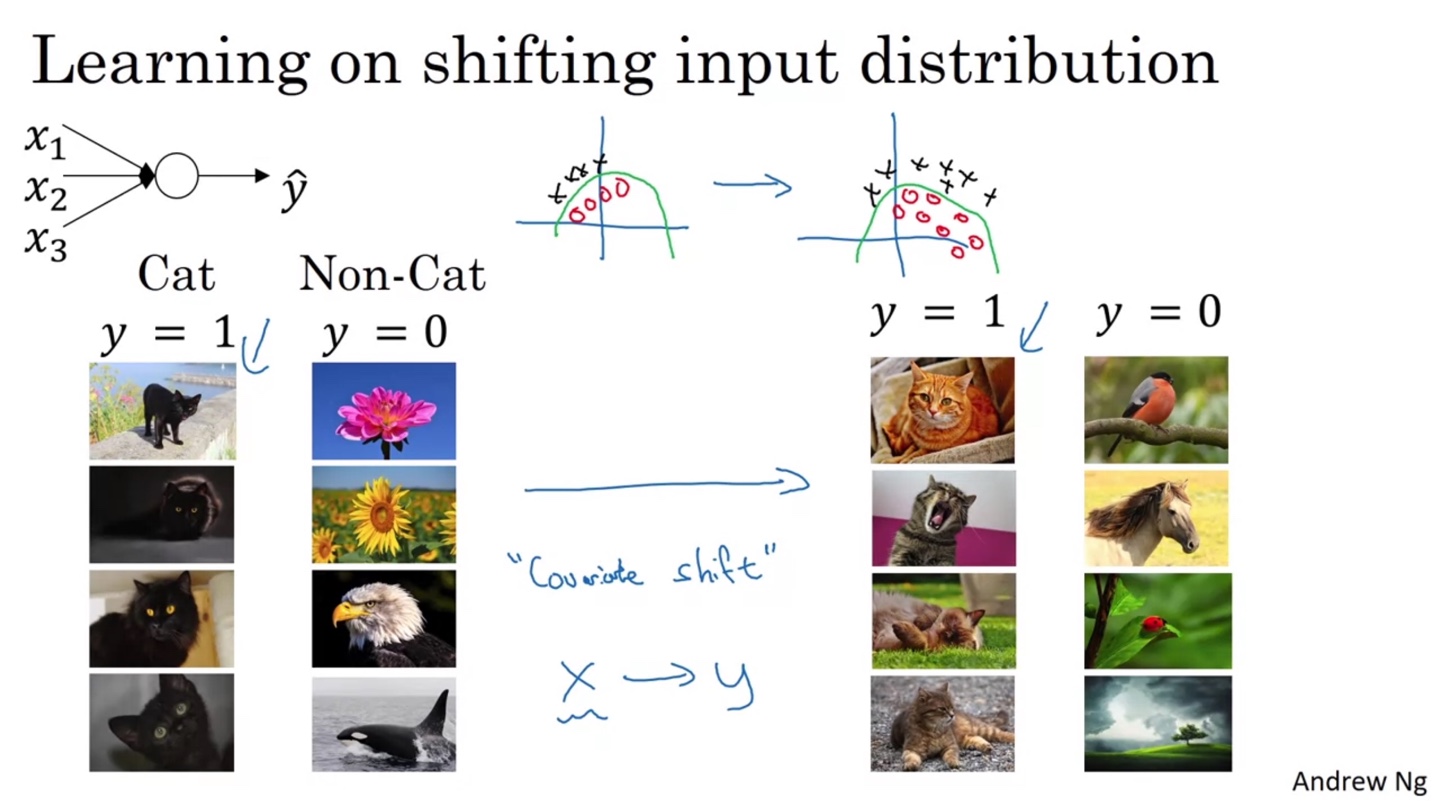
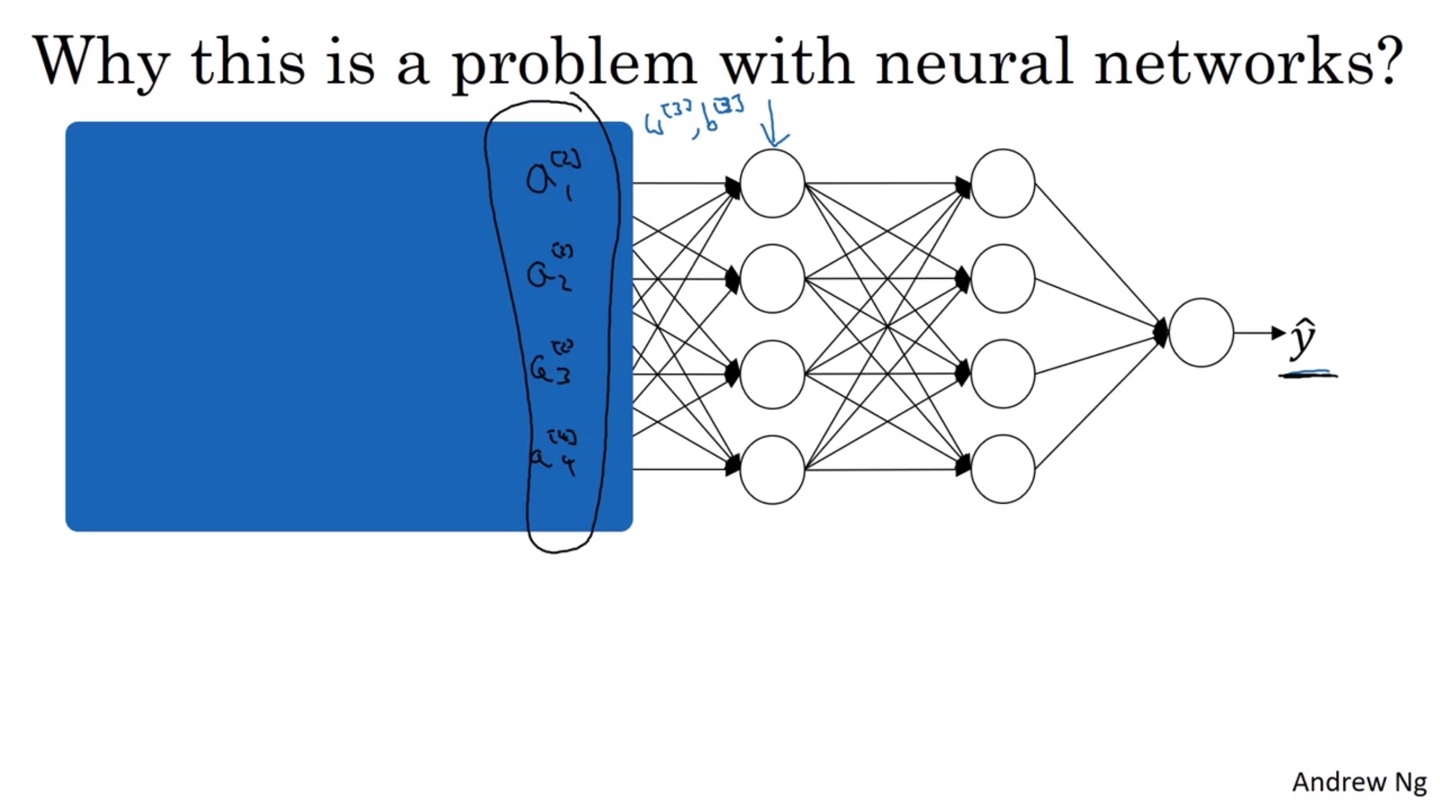
• Neural Network에서 어떠한 layer에 전달되는 값들은 바로 앞 layer에서 전달되어 오는 distribution과 다를 수 있다.

  • 이는 암막 커튼을 친 것과 같은 비유로 볼 수 있으며, 각 layer에서 Covariate Shift가 일어나는 것을 방지하기 위해 Batch Norm을 적용하는 것이다.

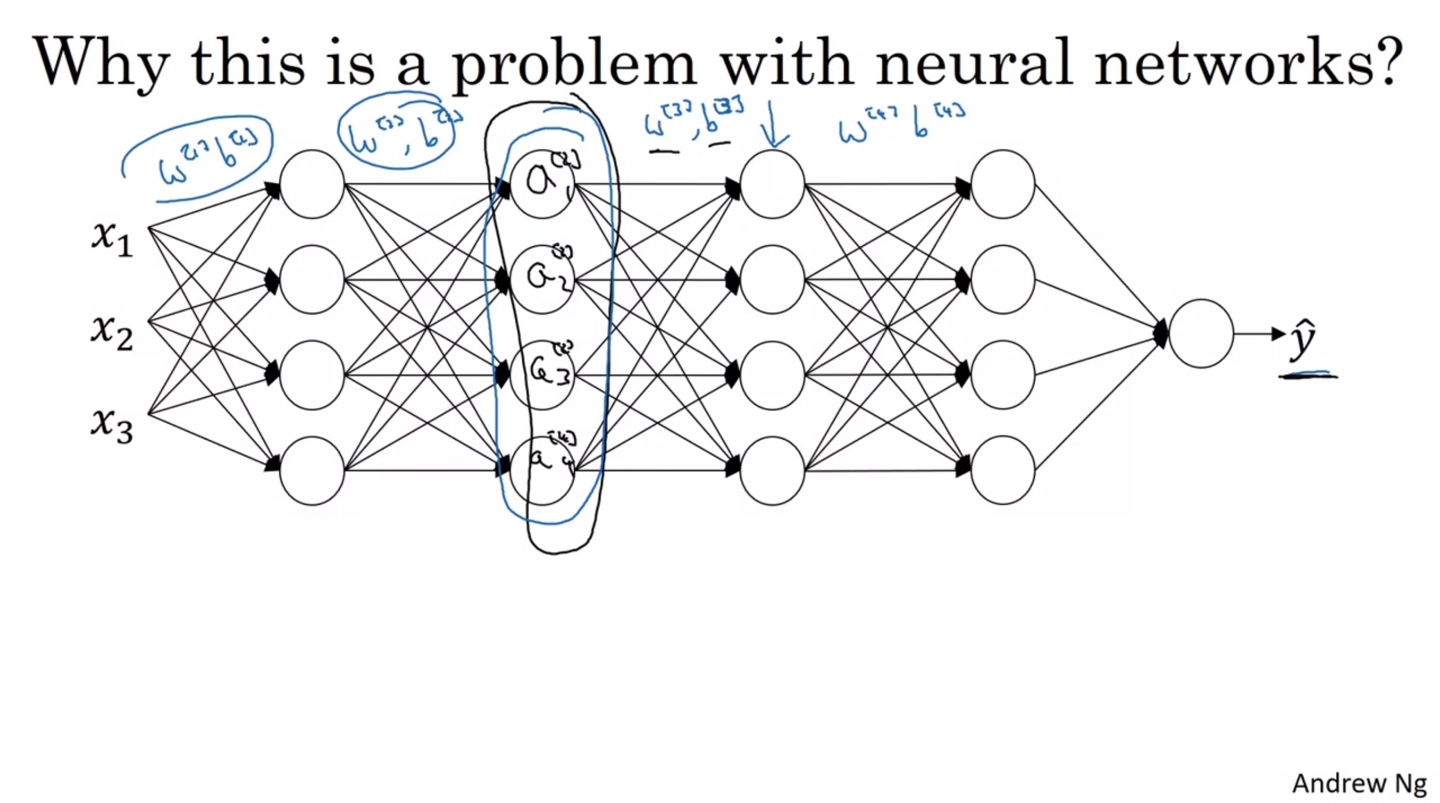
• Batch Norm을 활용하여 Mean이 0이고 Variance가 1인 분포로 만들면, 다음 layer로 전달할 때 $z$ 값의 분포가 어느 정도 일관성 있게 전달될 수 있다.

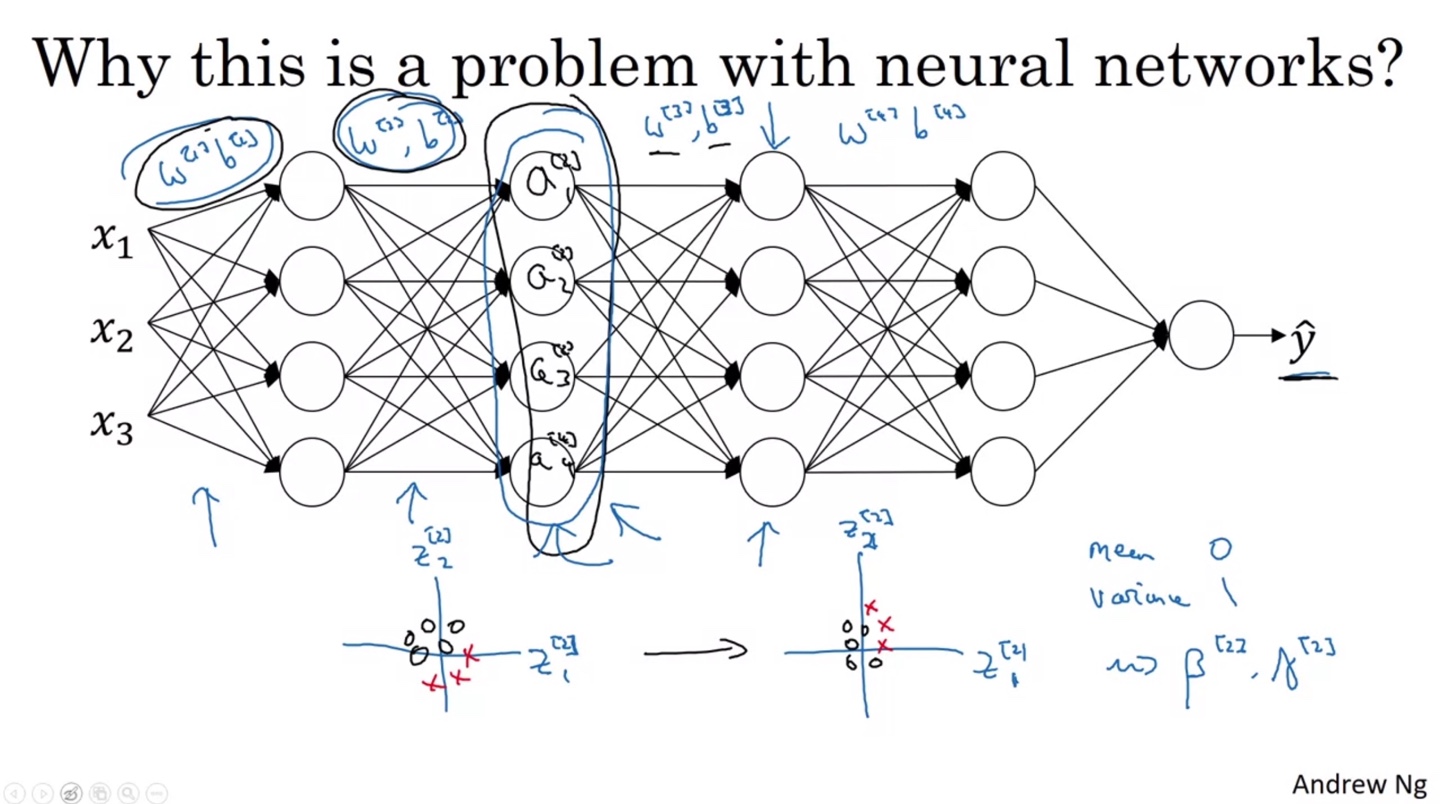
• 따라서 Batch Norm을 regularization과 같은 관점으로 바라보아도 된다.

  • 먼저 Mini-batch 단위로 mean/variance를 각각 계산하여 normalization을 적용한다.

  • $\beta$와 $\gamma$로 noise를 준 $\tilde{z}$로 넘겨주는 과정은 일종의 dropout과 비슷한 역할을 한다.

  • 이러한 과정 모두가 약간의 regularization 효과를 만들어낸다.

    • 그러나 batch size가 너무 작으면 효과가 미미하다는 단점이 존재한다.

Batch Norm at Test Time

• Test시 Batch Norm을 적용하는 방법은 다음과 같다.

  • 우선 Training시와 마찬가지로 mean과 variance를 구하고 $\epsilon$으로 분모를 조정한 뒤, $\beta$와 $\gamma$로 learnable parameter를 곱하여 $\tilde{z}$를 각 layer마다 구한다.

  • Test set의 mini-batch는 1개로 두고, 모든 test set의 $\mu$를 먼저 구한 뒤 test set 하나하나 마다의 Batch norm을 구하여 layer를 통과시킨다.

Multi-class Classification

Softmax Regression

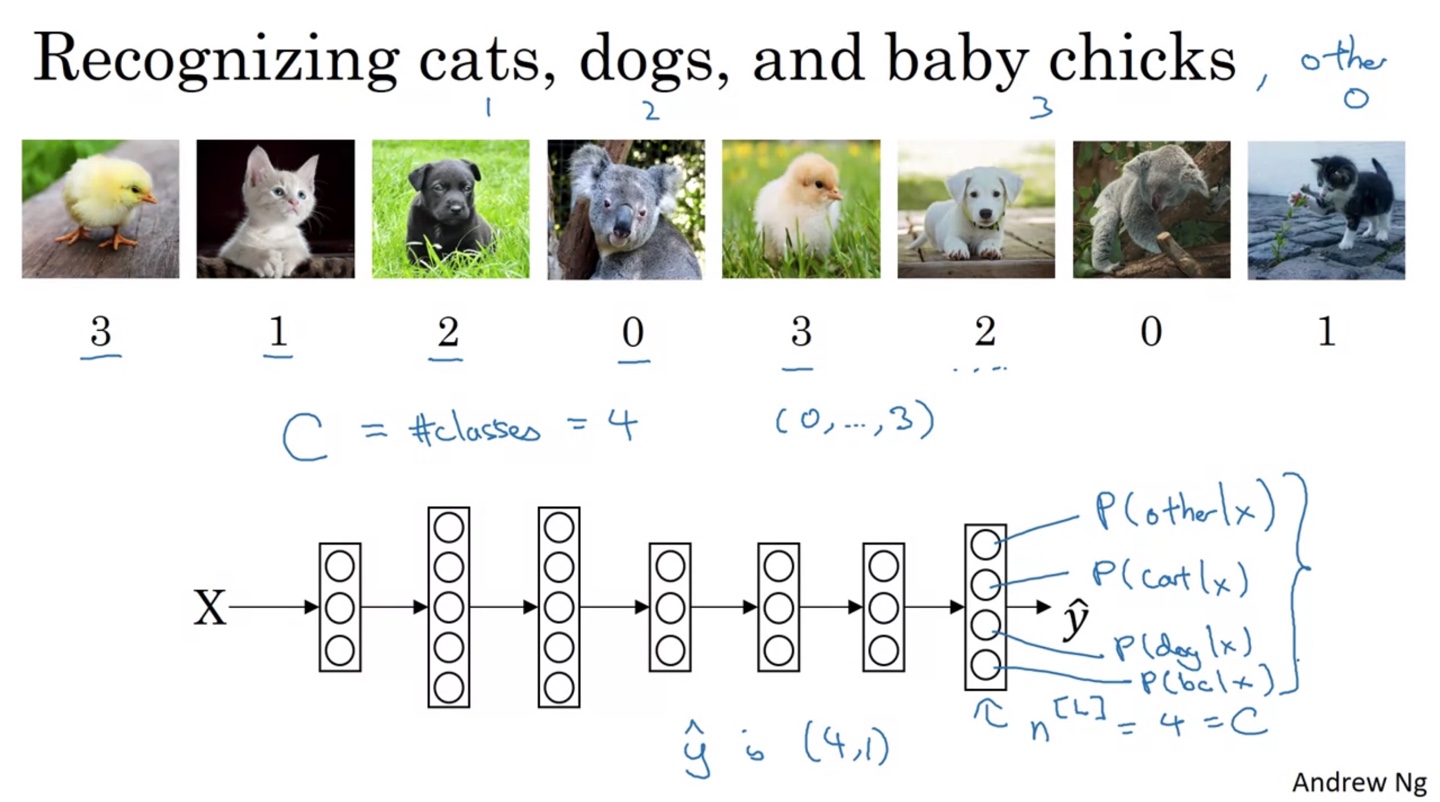
• 이번에는 고양이, 강아지, 병아리 그리고 다른 동물들로 Classification하는 task를 해결해보자.

  • 전체 classes의 개수는 4이며 최종 결과는 (0, ..., 3) 각각의 label일 확률을 구해, 이 중 가장 최대가 되는 label을 결정지어야 한다.

    • 따라서 마지막 layer의 node 개수 $n$과 예측값 $\hat{y}$의 shape은 (4, 1)을 띤다.

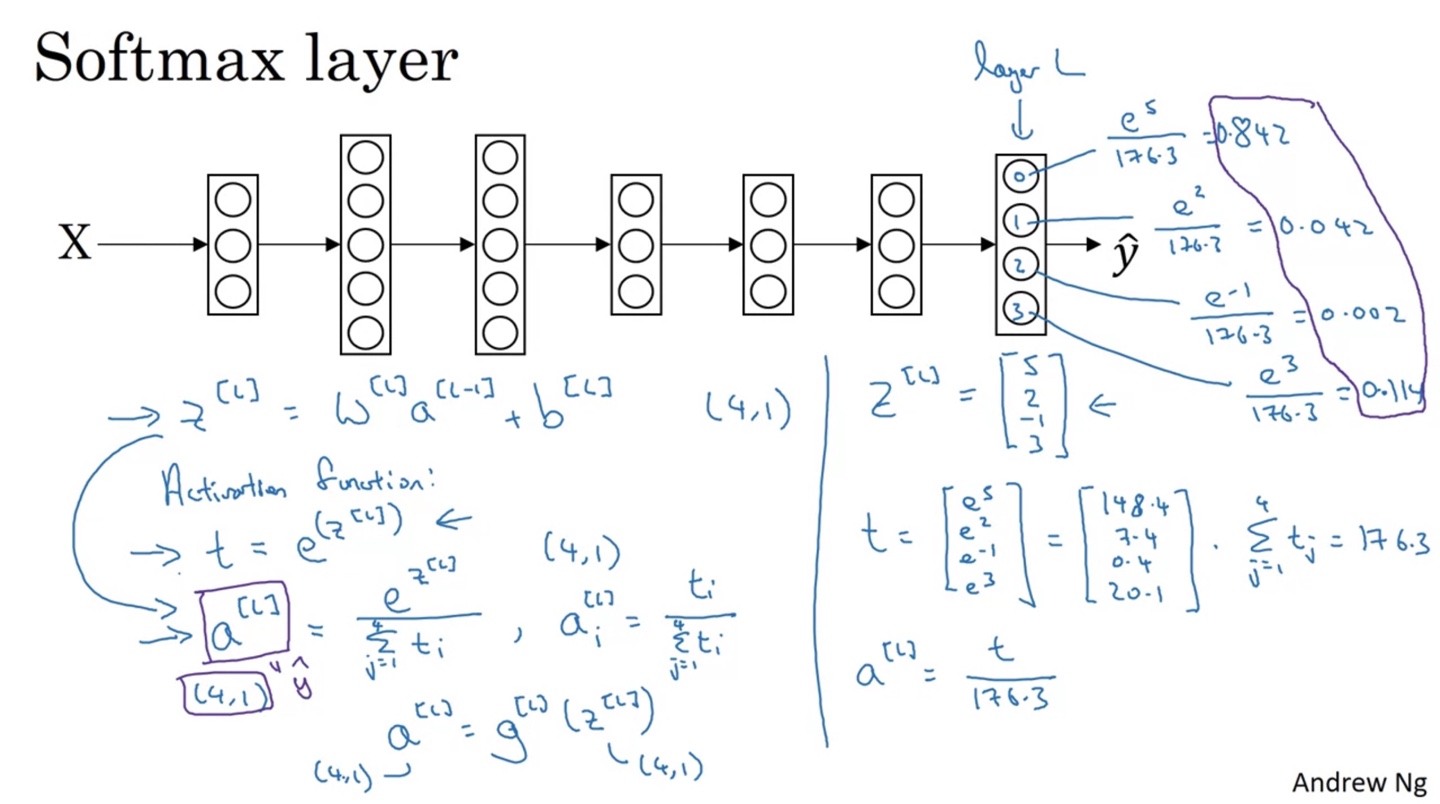
• Softmax를 Activation function으로 갖는 계산 과정은 다음과 같다.

  • 선형 변환인 $z$를 계산한 뒤 exponential을 취한다. → $t = e^{z^{[L]}}$

  • Class 개수인 4개의 $t_j$를 계산한 뒤 모두 더한 값을 분모로, 한 node의 $t_j$를 분자로 하는 activation $a^{[L]}$를 구한다. → $\displaystyle \frac{t_j}{\sum_{j=1}^{4} t_j}$

    • 이로써 $a^{[L]}$은 $g^{[L]}(z^{[L]})$임을 알 수 있고, $z$가 (4, 1)의 shape을 가지므로 $a$ 또한 (4, 1)의 shape을 가진다.

  • 만약 $z^{[L]}$가 $[5, 2, -1, 3]$의 값을 가진다면 exp을 취해 구한 $t$는 $[148.4, 7,4, 0.4, 20.1]$로 구해진다. → $\sum_{j=1}^{4} t_j = 176.3$

    • 전체 합을 분모로 하고 자신의 $t$값을 분자로 하는 수를 계산하면 $[0.842, 0.042, 0.002, 0.114]$로 계산되며, 이는 각 class일 확률을 나타낸다.

    • $a^{[L]}$ layer의 모든 값을 더하면 1이다. → 확률의 역할을 한다.

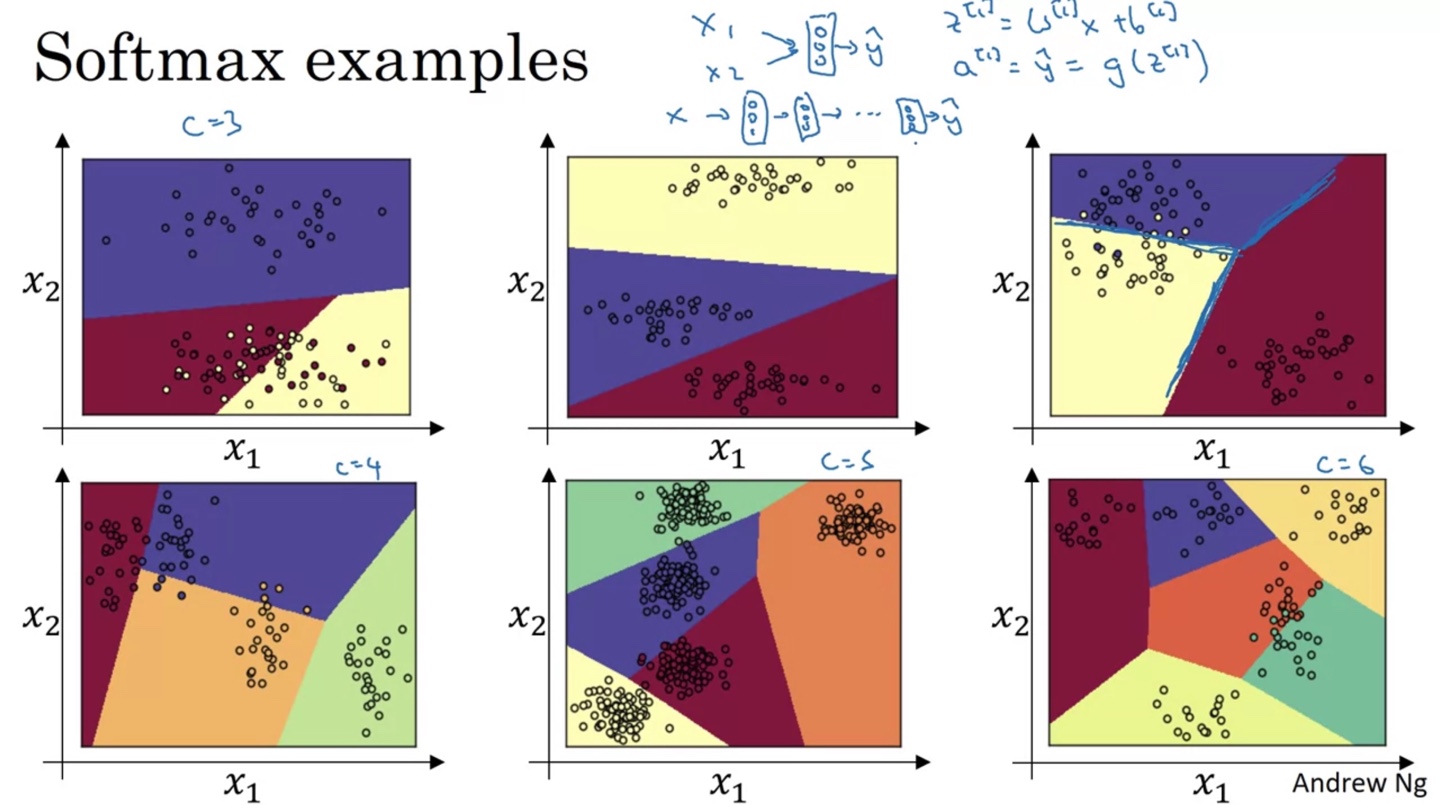
• Softmax는 구별하고자 하는 class의 개수에 따라 boundary가 다음과 같이 다양하게 결정된다.

  • 마지막 layer의 node 개수는 항상 classes 개수와 같아야 한다. ($\hat{y}$)

Training a Softmax Classifier

• Softmax Classifier의 마지막 layer를 hard max 취하면 0과 1로 정답 label을 구별지을 수 있다.

  • 만약 $C=2$라면 logistic regression으로 치환하는 것도 가능하다.

• 우리는 Loss function을 다음과 같이 정의할 것이다.

  • $L(\hat{y}, y) = - \displaystyle \sum_{j=1}^{4} y_j log \hat{y_j}$

    • 정답 label이 0과 1로 구별되기 때문에 정답일 logit의 확률 값이 클수록 loss는 줄어들게 만드는 것이다. → If C=2, $L =-y_2 log \hat{y_2} = -log \hat{y_2}$

    • 이는 곧 $\hat{y_2}$가 커지도록 학습하는 과정이다.

  • $Y$는 label이 4개 중에 하나로 결정되며 training set이 m개이므로 (4, m)의 shape을 띤다.

    • $\hat{y}$ 또한 마찬가지로 (4, m)의 shape을 가진다.

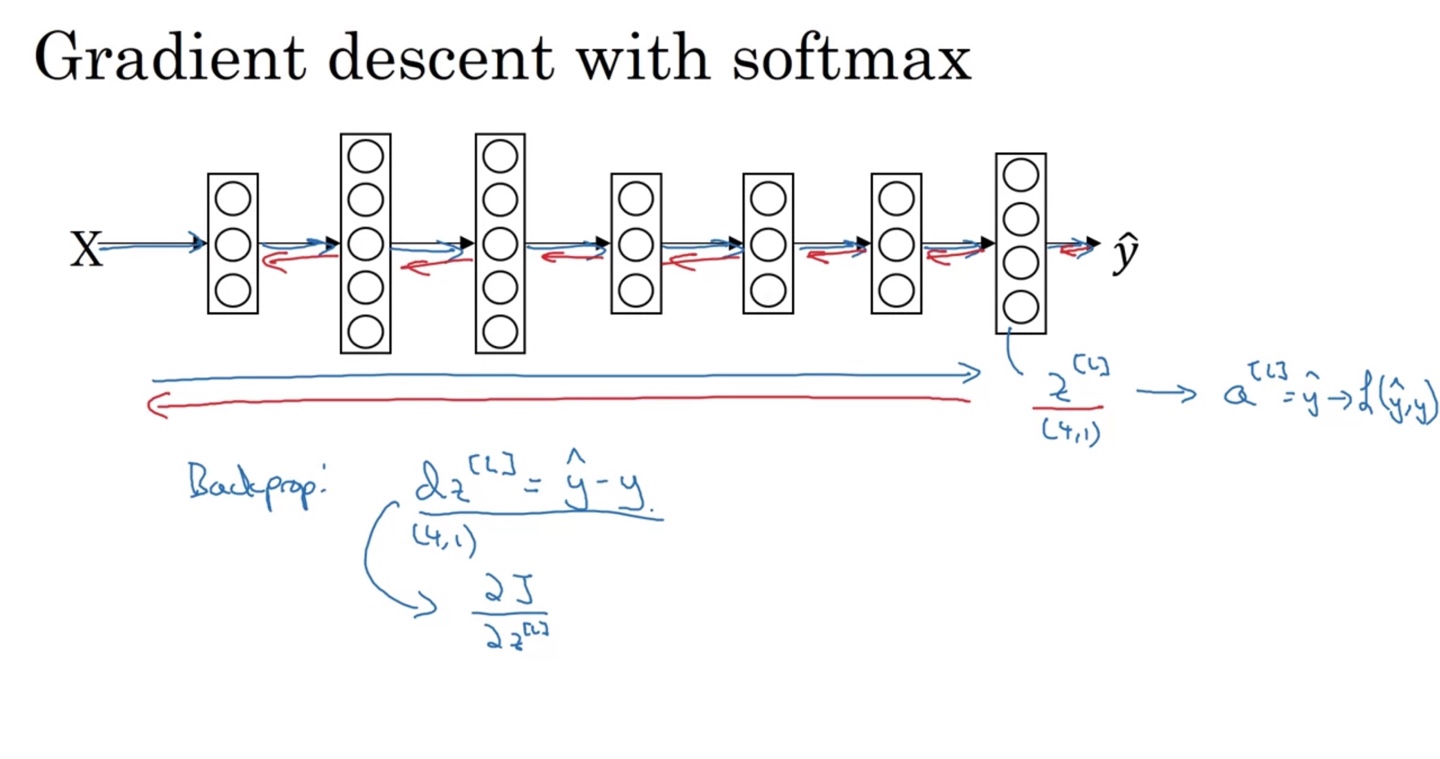
• Softmax를 최종 activation으로 갖는 gradient descent는 위에서 살펴보았던 Cross Entropy Loss를 활용하여 backpropagation을 진행한다.

  • $\displaystyle \frac{\partial{J}}{\partial{z^{[L]}}} = dz^{[L]} = \hat{y} - y$의 식을 활용하여 Back prop에 활용한다는 점을 알아두자.

---

• 출처: [Coursera] Deep Learing Specialization