Lecture 10: Expectation Continued

Proof of Linearity

• Let $T = X + Y$, show $E(T) = E(X) + E(Y)$

  • $\displaystyle \sum_{t} t P(T=t) \; ?= \displaystyle \sum_{x} x P(X=x) + \displaystyle \sum_{y} y P(Y=y)$

  • If it dependent, represented by $P(T=t) = \displaystyle \sum_{x} P(T=t | X=x) P(X=x)$

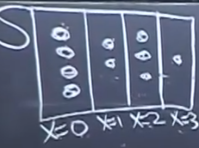
  • In pebble world, Expectation value is

    1) Grouped : $\displaystyle \sum_{x} x P(X=x)$ ← 그룹별 x에 대해
    2) Ungrouped : $\displaystyle \sum_{s} X(s) P({s})$ ← 개별 조약돌 s에 대해

  

• Proof of linearity (discrete case)

  • $E(T) = \displaystyle \sum_{s} (X+Y)(s) P({s}) = \displaystyle \sum_{s} (X(s) + Y(s)) P({s})$

    $= \displaystyle \sum_{s} X(s) P({s}) + \displaystyle \sum_{s} Y(s) P({s})$ ← each pabbles in X or Y!

• Similarity, $E(cX) = cE(X)$ if c is const.

• Extreme case of dependence : $X=Y$. Then $E(X+Y) = E(2X) = 2E(X) = E(X) + E(Y)$

Negative Binomial parmeters r, p

• Story : indep. Bern(p) trials, # failures before the rth success.

• Example, there are r=5 success, n=11 failure.

• PMF : $P(X=n) = \begin{pmatrix}n+r-1\\r-1\\ \end{pmatrix} p^r (1-p)^n$, for $n = 0, 1, 2, ...$

• $E(X) = E(X_1 + ... + X_r) = E(X_1) + ... E(X_r) = r \frac{q}{p}$

  • $X_j$ is # of failures between (j-1)st and jth success: $X_j \sim Geom(p)$

  • $r \frac{q}{p}$ : failure(p) 중 r번의 success(q)를 기다리는 일!

• What's the distribution of first success?

  • $X \sim FS(p)$ time until 1st success, counting the successes.

  • Let $Y = X-1$ $E(X) = E(Y) + 1 = \frac{q}{p} + 1 = \frac{1}{p}$

    • if p = 10, 10번의 시도로 1번의 성공을 만든다면 최소한 10번은 시도해야 함!

Putnam

• It's a very hard exam, there is one of that examples.

• Random permutation of 1, 2, ... n, where n \ge 2.

  • Fine expected # of local maxima. 3214756

• Let I, be indicator r.v. of position j having a local max, $1 \le j \le n$

  • if there is 3214756 here, 4와 5 사이에 큰 수가 주어진다고 하면 확률은 1/3이다. not 1/4 (4: 1/2 * 5: 1/2)!

  • $E(I_1 + ... + I_n) = E(I_1) + ... E(I_n) = \frac{n-2}{3} + \frac{2}{2} = \frac{n+1}{3}$

    • n-2개의 중간 지점에 1/3의 확률 + 맨 끝 지점에 1/2 확률

    • 간단한 상황 : n=2, [1 2][2 1] → $E(X) = 1$

    • 극단적 상황 : n→∞, → $E(X) = ∞$
      

St. Petersburg Paradox

• Get $ $2^X$, where X is # flips of fair coin until first H, including the successes.

• $Y = 2^X$(받는 돈), find E(Y).

  • $E(Y) = \displaystyle \sum_{k=1}^{∞} 2^k • \frac{1}{2^k} = \displaystyle \sum_{k=1}^{∞} 1 = 1+1+1+1 ... = ∞$

  • bound at $$2^{40}$, then $\displaystyle \sum_{k=1}^{40} 2^k • \frac{1}{2^k} = 40$

  • $$2^{40}$를 받기 위해서는 40번을 던져야 한다.

• Be careful, $∞ = E(2^X) \ne 2^{E(X)} = 4$ : This is not linearity!

• 출처 : Statistics 110, boostcourse