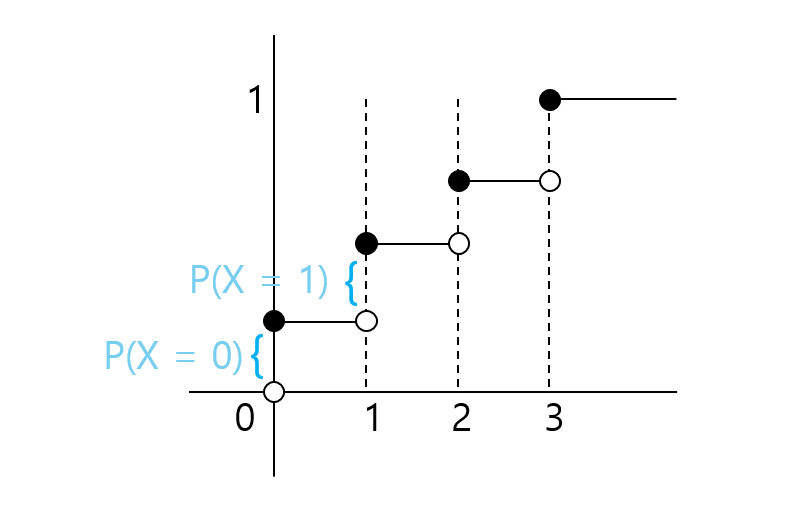Lecture 9: Expectation, Indicator Random Variables, Linearity

CDF

• CDF(누적 분포 함수)

  : $F(x) = P(X \le x)$, as a function of real x.

  

• Find $P(1 < X \le 3)$ using F

  : $P(X \le 1) + P(1 < X \le 3) = P(X \le 3)$

  $\Rightarrow P(1 < X \le 3) = F(3)-F(1)$

  • in general, $P(a < X \le b) = F(b)-F(a)$

• Properties of CDF

  (1) increasing

  (2) right continuous

  (3) $F(x) → 0 \; as \; x → -∞$, $F(x) → ∞ \; as \; x → ∞$.

  • This is "if and only if" : 필요 충분 조건

• Indep. of random variables

  • X, Y are indep. r.v.s if $P(X \le x, Y \le y) = P(X \le x)P(Y \le y)$ for all x, y.

  • Discrete case : $P(X=x, Y=y) = P(X=x)P(Y=y)$

Averages(Means, Expected values)

• $1, 2, 3, 4, 5, 6 → \frac{1+2+3+4+5+6}{6} = 3.5 = \frac{1+6}{2}$

  • in Gauss raw, $\frac{1}{n} \displaystyle \sum_{j=1}^{n} j = \frac{n+1}{2}$

• | 1, 1, 1, 1, 1, | 3, 3, | 5

  • Two ways

    (1) add, divide by 8

    (2) Weighted Average: $\frac{5}{8}•1 + \frac{2}{8}•3 + \frac{1}{8}•5$

    • weight is probability!

• Average of a discrete r.v.X

  • $E(X) = \displaystyle \sum_{x} xP(X=x) : (value)(PMF)$,
    summed over x with $P(X=x) > 0$

• $X \sim Bern(p)$

  : $E(X) = 1P(X=1) + 0P(X=0) = p$

  • $X = \begin{cases} 1, & {if\; A \; occurs} \\ 0, & {otherwise} \\ \end{cases}$ (indicator r.v.)

  • Then $E(X)=P(A)$ fundamental bridge

    → X를 지시 확률 변수라 생각할 수 있음

• $X \sim Bin(n, p)$

  : $E(X)= \displaystyle \sum_{k=0}^{n} k \begin{pmatrix}n\\k\\ \end{pmatrix} p^{k} q^{n-k}$

  $= \displaystyle \sum_{k=1}^{n} n \begin{pmatrix}n-1\\k-1\\ \end{pmatrix} p^{k} q^{n-k}$

  $=np \displaystyle \sum_{k=1}^{n} \begin{pmatrix}n-1\\k-1\\ \end{pmatrix} p^{k-1} q^{n-k}$

  $=np \displaystyle \sum_{j=0}^{n-1} \begin{pmatrix}n-1\\j\\ \end{pmatrix} p^{j} q^{n-1-j}$ : $j=k-1, k=j+1$

  $\Rightarrow np$
  

• Linearity

  : $E(X+Y) = E(X) + E(Y)$

  • even if X, Y are dependent

  : $E(cX) = cE(X)$

  • if c is a const.

• Redo Bin

  • np, by linearly

  • since $X=X_1 + ... + X_n$, $X_j \sim Bern(p)$

• Ex. 5 card hard, X=(# of aces).

  • Let $X_j$ be indicator of jth card being our ace, $1 \le j \le 5$

  • $E(X)= E(X_1 + ... + X_5) = E(X_1) + ... + E(X_5) = symmetry \; 5E(X_1)$

    fund. bridge, $= 5P(1st \; card \; ace) = \frac{5}{13}$, even though $X_j$'s are dependent.

  • This gives expected value of any Hypergeometric.

• Geom(p)

  : indep. Bern(p) trials, count # failures before 1st success.

  ex. F F F F F S : $P(X=5) = q^{5} p$

  • Let $X \sim Geom(p), \; q=1-p$.

  • PMF: $P(X=k)=q^{k} p$, $k \in \{0, 1, 2, ...\}$

    valid since $\displaystyle \sum_{k=0}^{∞} pq^{k} = p\displaystyle \sum_{k=0}^{∞} q^{k} = \frac{p}{1-q} = 1$ (기하 급수)

• $X \sim Geom(p)$

  : $E(X) = \displaystyle \sum_{k=0}^{∞} kpq^{k}$

  • cf. $\displaystyle \sum_{k=0}^{∞} q^{k} = \frac{1}{q}$ ← derivative

    $\Rightarrow \displaystyle \sum_{k=0}^{∞} = kq^{k-1} \frac{1}{(1-q)^2}$

    $\Rightarrow \displaystyle \sum_{k=0}^{∞} kq^{k} = \frac{q}{(1-q)^2}$

• Story Proof

  • Let $c=E(X)$

  • $c = 0•p + (1+c)•q = q + cq$

    $\Rightarrow c = \frac{q}{1-q} = \frac{q}{p}$

• 출처 : Statistics 110, boostcourse