Lecture 12: Discrete vs. Continuous, the Uniform

Intoduction

Discrete	Continuous
$X$	$X$
PMF $P(X=x)	PDF $f_x(x)$ [$P(X=x) = 0$]
CDF $F_x(x) = P(X \le x)$	CDF $F_x(x) = P(X \le x)$
$E(X) = \displaystyle \sum_{x} P(X=x)$	$E(X) = \int_{-∞}^{∞} sf_x(x) dx$
$V(X) = E(X^2) - (EX)^2$	$V(X) = E(X^2) - (EX)^2$
$sd(X) = \sqrt{Var(X)}$	$sd(X) = \sqrt{Var(X)}$
LOTUS $E(g(X)) = \displaystyle \sum_x g(x) P(X=x)$	LOTUS $E(g(X)) = \displaystyle \sum_x g(x) P(X=x)$

PDF (probability density function)

• Defn

  • R.V $X$ has PDF $f(x)$ if $P(a \le X \le b) = \int_{a}^{b} f(x)dx$

  • For all a, b [$a=b \Rightarrow \int_{a}^{a} f(x)dx = 0$]

    • To be valid, $f(x) \ge 0$, $\int_{-∞}^{∞} f(x)dx = 1$

  • $f(x_0)\; • \; \epsilon \approx P(X \in (x_0 - \displaystyle \frac{\epsilon}{2}, x_0 + \displaystyle \frac{\epsilon}{2})$ for $\epsilon > 0$ very small.

    • This is the density

    

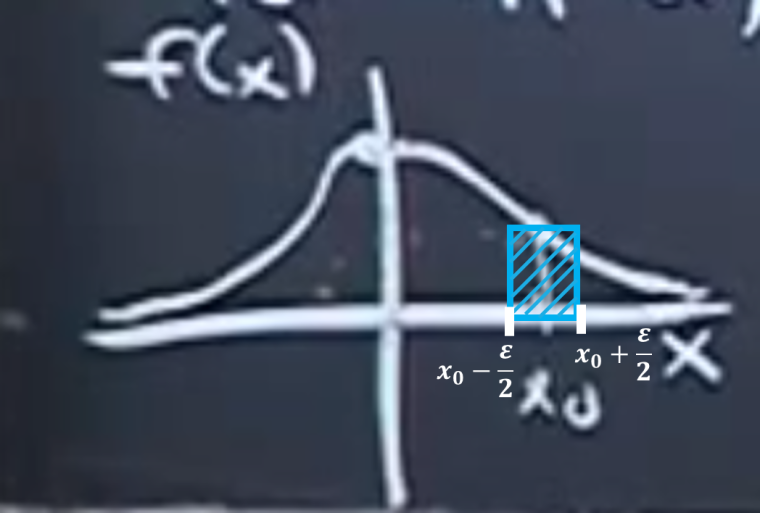
• If $X$ has PDF f, the CDF is $F(x) = P(X \le x) = \int_{-∞}^{x} f(t)dt$ ($t$ is the dummy variable, not conflict with $x$)

  

• If $X$ has CDF, F(and X is continuous), then

  • $f(x) = F'(x)$ by FTC(Fundamental Theorom of Calculus). <derivative>

• $P(a < X < b) = \int_{a}^{b} f(x) dx = F(b) - F(a)$ by FTC

Variance

• $Var(X) = E(X-EX)^2$

  • Variance가 절댓값 형태가 아닌 이유는 다루기 복잡해서다 (미분 불가 때문).

• Standard deviation : $SD(X) = \sqrt{Var(X)}$

• Another way to express Var :

  • $Var(X) = E(X^2 - 2X(EX) + (EX)^2)$

    $= E(X^2) - 2E(X)EX + (EX)^2 = E(X^2) - (EX)^2$

  • Notation : $EX^2 = E(X^2)$

Unif(a, b)

• Completely "random point in [a, b]"

  

• Unif : prob. $\propto$ length.

  • 중심을 기준으로 대칭 → 길이에 따라 확률이 커짐!

• PDF

  • $f(x) = \begin{cases} c, & {if \; a \le x \le b} \\ 0, & {otherwise} \end{cases} \Rightarrow 1 = \int_{a}^{b} cdx = c(b-a), \; c = \displaystyle \frac{1}{b-a}$

• CDF

  • $F(X) = \int_{-∞}^{x} f(t) dt = \int_{a}^{b} f(t) dt = \begin{cases} 0, & {if \; x < a} \\ \displaystyle \frac{x-a}{b-a}, & {if a \le x \le b} \\ 1, & {if \; x > b} \end{cases}$

• Expective

  • $E(X) = \int_{a}^{b} = \displaystyle \frac{x}{b-a} dx = \displaystyle\frac{x^2}{2(b-a)} \biggr|_{a}^{b} = \frac{1}{2(b-a)} (b-a)(b+a)$

    $= (a+b) / 2$

  • Expectation is mid point! (intuitive answer)

• Variance

  • If $Y=X^2$, $E(X^2) = E(Y)$ need PDF of Y?

    • $\int_{-\infty}^{\infty} x^2 f_x(x) dx$

  • Law of the unconscious statistician(무의식 통계학자의 법칙) (LOTUS)

    • $E(g(X)) = \int_{-\infty}^{\infty} g(x) f_x(x) dx$

  • Let $U \sim Unif(0, 1)$, $E(U) = 1/2$, $E(U^2) = \int_{0}^{1} U^2 f_u(u) du$

    • $f_u(u) du$ is constant, $E(U^2) = \int_{0}^{1} U^2 \; • \; 1 = 1/3$

    • $Var(U) = E(U^2) - (EU)^2 = 1/3 - 1/4 = 1/12$

Uniform is universal

• Uniform을 통해 모든 확률 분포를 알 수 있다.

  • Let $U \sim Unif(0, 1)$, $F$ be a CDF(assume F is strictly increasing continous <F는 연속인 증가함수>)

• Theorm

  • Let $X = F^{-1}(U)$, Then $X \sim F$

• Proof

  • $P(X \le x) = P(F^{-1}(U) \le x) = P(F(F^{-1}(U)) \le F(x)) P(U \le F(x))$

    $= P(U \le F(x)) = F(X)$

    • Unif(0, 1)에서 x까지의 확률은 간격의 길이임!

    

---

• 출처 : Statistics 110 boostcourse