Lecture 13: Normal distribution

Universality of Uniform

• Let F be a continuous, strictly increasing CDF

  • Then $X=F^{-1} \sim F$ if $U~Unif(0, 1)$

    • It used in Diffusion model ans Simulating some distribution

  • Also: if $X \sim F$, Then $F(X) \sim Unif(0, 1)$

    • $F(X) = P(X \le x)$,

      $F(x) = 1-e^{-x}$, $x>0$ $\Rightarrow F(X) = 1-e^{-X}$

• Example

  • Let $F(x) = 1-e^{-x}$, $x>0$ (Expo(1)), $U \sim Unif(0, 1)$

  • Simulate $X \sim F$, $F^{-1}(u) = -ln(1-u) \Rightarrow F^{-1}(u) = -ln(1-u) \sim F$

    • $1-u \sim Unif(0, 1)$ (symmetry of Unif)

    • $a+bu \sim Unif(a, a+b)$ Unif on same interval (linear transform of Unif)

      • non-linear usually → non-Unif !

Indep. of r.v.s $X_1, ... , X_n$

• Defn in Continuous case:

  • $X_1, ... , X_n$ indep if $P(X_1 \le x_1, ... X_n \le x_n)$

    $= P(X_1 \le x_1) ... P(X_n \le x_n)$ for all $x_1, ... x_n$

• Defn in Discrete case:

  • Joint PMF $P(X_1=x_1, ... X_n=x_n)$

    $= P(X_1=x_1) ... P(X_n = x_n)$ for all $x_1, ... x_n$

• Example

  • $X_1, X_2 \sim Bern(\displaystyle \frac{1}{2})$ i.i.d, $X_3 = \begin{cases} 1, & {if \; X_1=X_2} \\ 0, & {otherwise} \end{cases}$

  • These are pairwise indep, not indep.

    • ($X_1$, $X_2$), ($X_2$, $X_3$), ($X_1$, $X_3$) is indep, but not ($X_1$, $X_2$, $X_3$) indep!

    • After determined $X_1$ and $X_2$, and possible to know $X_3$

Normal distribution (By Gauss)

Central Limit Thm: Sum of a lot of i.i.d. r.v.s looks Normal

• $N(0, 1)$ has PDF $f(z) = ce^{-z^2/2}$, c is normalizing const.

  

• Intergal function $f$

  • $\int_{-∞}^{∞} e^{-z^2/2} dz$ → 부정적분이므로 닫힌 형태로의 적분이 불가능!

  • $\int_{-∞}^{∞} e^{-z^2/2} dz \int_{-∞}^{∞} e^{-z^2/2} dz$

    $= \int_{-∞}^{∞} e^{-x^2/2} dx \int_{-∞}^{∞} e^{-y^2/2} dy$

    $= \int_{-∞}^{∞} \int_{-∞}^{∞} e^{-(x+y)^2/2} dxdy$

    $= \int_{0}^{2 \pi} \int_{0}^{∞} e^{-r^2/2} r dr d \theta$, $r^2 = x^2 +y^2$ ($r dr d \theta$ is Jacobian matrix)

    

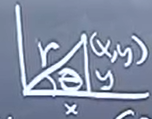
  • Let $u=r^2/2$ & $du=rdr$

    $= \int_{0}^{2 \pi} (\int_{0}^{∞} e^{-u} du) d \theta = \int_{0}^{2 \pi} (1) d \theta = 2 \pi$

    $\int_{-∞}^{∞} e^{-z^2/2} dz = \sqrt{2 \pi}$

• Normalizing constant c = $\displaystyle \frac{1}{\sqrt{2 \pi}}$

Expectation & Variance

• $Z \sim N(0, 1)$, $EZ = E(Z) = \displaystyle \frac{1}{\sqrt{2 \pi}} \int_{-∞}^{∞} ze^{-z^2/2} = 0$ by symmetry

  • if $g(x)$ is an odd fn, i.e. $g(-x) = -g(x)$ then $\int_{-a}^{a} g(x)dx = 0$

    

• $Var(Z) = E(Z^2) - (EZ)^2 = E(Z^2)

  • $\displaystyle \frac{1}{\sqrt{2 \pi}} \int_{-∞}^{∞} z^2 e^{-z^2/2} dz$ <even fn>

    $= 2 \displaystyle \frac{1}{\sqrt{2 \pi}} \int_{0}^{∞} z^2 e^{-z^2/2} dz$

    $= 2 \displaystyle \frac{1}{\sqrt{2 \pi}} \int_{0}^{∞} zz e^{-z^2/2} dz$

  • Let $u=z$ & $du=dz$, $v= -e^{-z^2/2} dz$ & $dv = z e^{-z^2/2}$

    $= 2 \displaystyle \frac{1}{\sqrt{2 \pi}} \displaystyle((uv)\biggr|_{0}^{∞} + \int_{0}^{∞} e^{-z^2/2} dz) = 1$

    • $uv = ze^{-z^2/2} dz = 0•1 = 0$, $\int_{0}^{∞} e^{-z^2/2} dz = \sqrt{2 \pi}$

Notation

• \Phi is the standard Normal CDF

  • $\Phi(z) = \displaystyle \frac{1}{\sqrt{2 \pi}} \int_{-∞}^{z} e^{-t^2/2} dt$

  • $\Phi(-z) = 1 - \Phi(z)$ by symmetry

• 출처 : Statistics 110, boostcourse