Lecture 23: Beta distribution

Beta distribution

• $Beta(a, b)$, $a>0, b>0$

  • PDF: $f(x) = cx^{a-1}(1-x)^{b-1}$, $0 < x < 1$

• Features

  • "Flexible" family of continuous distributions on $(0, 1)$

    (1) if $a=b=1$, contant function
    (2) if $a=2, b=1$, linearly function
    (3) if $a=\displaystyle \frac{1}{2} =b$, power function
    (4) if $a=b=2$, inverse of power function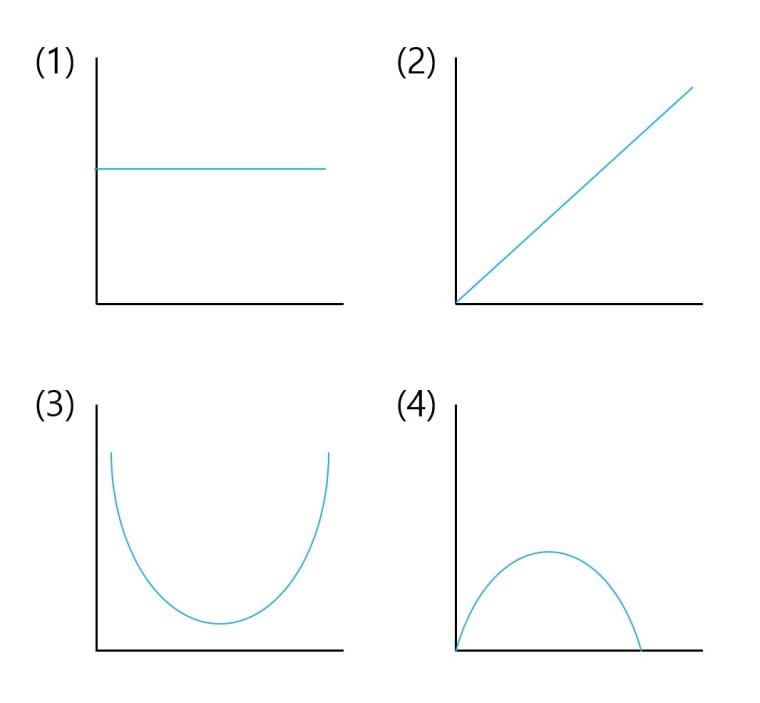

    

  • Often used as prior(사전 확률) for parameter in $(0, 1)$

  • 'conjugate prior to Binomial' (사전과 사후가 모두 Beta distribution을 따른다!)

  • connections to other distributions

Conjugate prior for Binomial

• $X |\; p \sim Bin(n, p)$,

  • $p \; | Beta(a, b)$ [prior]

• Find posterior distributino(사후 분포) $p \; | X$

  • $f(p \; | X=k) = \displaystyle \frac{P(X=k | \; p) f(p)}{P(X=k)}$

    • $P(X=k)$ does not dependent p.

    $= \displaystyle {n \choose k} p^k (1-p)^k \subset p^{a-1} (1-p^{b-1}) / P(X=k)$

    $\propto p^{a+k-1} (1-p)^{b+n-k-1}$

    $p \; | X \sim Beta(a+X, b+n-X)$

    • $X$ 성공 횟수, $n-X$ 실패 횟수로 취급해보라.

  • if $a=b=1$, 라플라스 계승 법칙을 따른다.