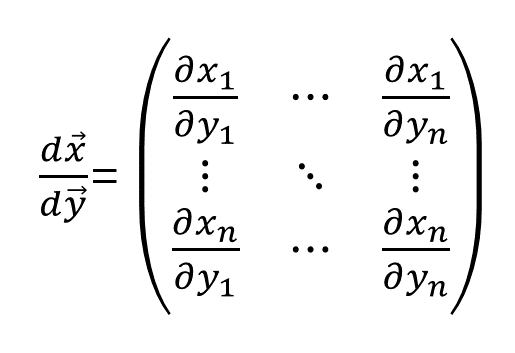Lecture 22: Transformations and Convolutions

Previous 21th review

• Variance of Hypergeom(w, b, n)

  • $p = \displaystyle \frac{w}{w+b}$, $w+b = N$

• $Var(\displaystyle \sum_{j=1}^{n} X_j) = Var(X_1) + ... + Var(X_n) + 2 \sum_{i<j} Cov(X_i, X_j)$

  $= np(1-p) + 2 \displaystyle {n \choose 2} \frac{w}{w+b} \frac{w-1}{x+b-1} - p^2$
  $= \displaystyle \frac{N-n}{N-1} np(1-p)$ ← finite population correation

  • $Cov(X_1, X_2) = E(X_1 X_2) - (EX_1) (EX_2)$
  • Extreme cases
    : $n=1$ → $Bern(p)$의 분산
    : $N$ much much larger than $n$, $\displaystyle \frac{N-n}{N-1} \approx 1$ → $Bin(n, p)$의 분산

Transformations

• Thm.

  • Let $X$ be a continuous r.v. with PDF $f_X$, $Y = g(X)$

    • $g$ is differentiable, strictly increasing.

  • Then the PDF of $Y$ is given by $f_Y(y) = f_X(x) \displaystyle \frac{dx}{dy}$ where $y = g(x)$, $x = g^{-1}(y)$ and this is written in terms of $y$.

    • Also, $\displaystyle \frac{dx}{dy} = (\frac{dy}{dx})^{-1}$ by chain rule.

• Proof.

  • CDF of $Y$ is

    $P(Y \le y) = P(g(X) \le y) = P(X \le g^{-1}(y)) = F_X(g^{-1}(y)) = F_X(X)$

    $\Rightarrow f_Y(y) = f_X(x) \displaystyle \frac{dx}{dy}$ [chain rule]

• Example. (log normal)

  • $Y = e^{Z}$. $Z \sim N(0, 1)$

    • $\displaystyle \frac{dy}{dz} = e^{z} = y$

    • $f_Y(y) = \displaystyle \frac{1}{\sqrt 2 \pi} e^{-(lny)^2 / 2}$ ← multiply by $\displaystyle \frac{dz}{dy}$

    • $f_Y(y) = \displaystyle \frac{1}{y} \frac{1}{\sqrt 2 \pi} e^{-(lny)^2 / 2}$, $y>0$ ← This is PDF.

Transformations in $R^n$

• $\vec{Y} = g(\vec{X})$, $g : R^n → R^n$ : n dimentional

  • $\vec{X} = (X_1, ... X_n)$ continuous.

• Joint PDF of $\vec{Y}$ is $f_{\vec{Y}}(\vec{y}) = f_{\vec{X}}(\vec{x}) |{\displaystyle \frac{d \vec{x}}{d \vec{y}}}|$ ← Jacobian, abs value of determinant.

  • $|{\displaystyle \frac{d \vec{y}}{d \vec{x}}}|^{-1} = |{\displaystyle \frac{d \vec{x}}{d \vec{y}}}|$
    

Convolution(sums)

• Let $T = X+Y$, $X$, $Y$ indep.

  • Discrete case : $P(T=t) = \displaystyle \sum_{x} P(X=x) P(Y=t-x)$

  • Continuous case : $f_T(t) = \int_{-∞}^{∞} f_X(x) f_Y(t-x) dx$

    • since $F_T(t) = P(T \le t) = \int_{-∞}^{∞} P(X+Y \le t | X=x) f_X(x) dx$

      $= \int_{-∞}^{∞} F_Y(t-x) f_X(x) dx$ ← 미분 먼저 하고 적분하기

• Idea : prove existence of objects with desired properties using prob.

  • Show $P(A) > 0$ for a random object.

Shannon Theory

• Suppose each object has a "score". Show there is an object with "good" score.

  • There is an object with score is at least $E(X)$ ← score of random object

• Ex.

  • 100 people, 15 committees of 20, each person is on 3 committees.

    • Show there exist 2 committees with overlap $\ge 3$.

  • Idea : find average overlap of 2 random committies.

    • $E(overlap) = 100 \times \displaystyle \frac{3 \choose 2}{15 \choose 2} = \frac{300}{(\frac{15 \times 14}{2})} = \frac{40}{14} = \frac{20}{7}$

    $\Rightarrow$ there exists pair of committies with overlap of $\ge \displaystyle \frac{20}{7}$
    $\Rightarrow$ have overlap of $\ge 3$

• 출처 : Statistics 110, boostcourse