Lecture 6: Monty Hall, Simpson's Paradox

Monty Hall, three doors problem

• Monty Hall : the game show host

• There are three doors, Monty hall ask to choose. (Monty knows which)

  • 1 door has car, 2 doors have goats

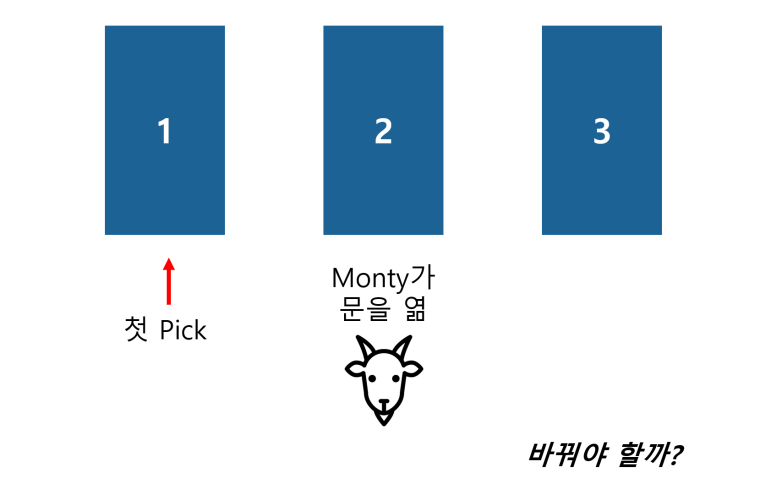
• Monty always open a goat door, if he has a choice, he picks with equal prob. Should you switch?

  • Note : If Monty opens Door 2, we know Door 2 has a goat, and Monty opened Door 2.

• The answer is YES! You should change!

  • The first time, you would pick it for 1/3 prob.

  • But after Monty picked one, it would be 2/3 prob. not 50/50 !

Approach 1: Tree

• Make a tree diagram, and remove paddles (with regularization)

  • $P(success \; if \; switch \; | \; Monty \; opens \; door \; 2) = \frac{2}{3}$

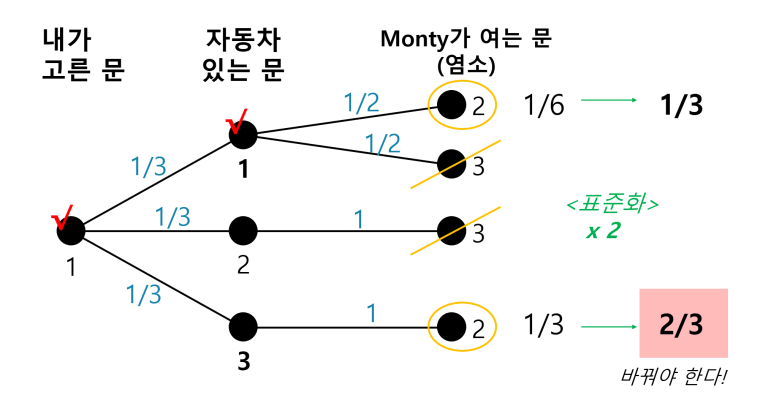
Approach 2: Law Of Total Probability

• LOTP : wish we know where the car is.

  • $S$ : succeed (assuming switch)

  • $D_j$ : Door j has the car $(j ∈ {1, 2, 3})$

  • $P(S) = P(S|D_1) \frac{1}{3} + P(S|D_2) \frac{1}{3} + P(S|D_3) \frac{1}{3}$

    $= 0 + 1 \frac{1}{3} + 1 \frac{1}{3} = \frac{2}{3}4$

  • By symmetry $P(S|Monty \; opens \; 2) = \frac{2}{3}$

Simpson's Paradox

• Conditional / Unconditional prob. definitely diffrent!

  • It would hard to success heart surgery rather than bandage remove surgury, so Dr. Hilbert is a good doctor!

  • But according to unconditional(무조건적) prob. , Dr.Nick has better prob. to success surgery...

  • You just do not doing that $\frac{1}{3} + \frac{2}{5} ≠ \frac{3}{8}$, paradox would not occur!

Non-naive approach

• A : successful surgery
  B : treated by Dr. Nick
  C : heart surgery

• $P(A|B, C) < P(A|B^c, C)$
  : success given Dr. Nick heart surgery < success given Dr. Hilbert heart surgery

• $P(A|B, C^c) < P(A|B^c, C^c)$
  : success given Dr. Nick bandage surgery < success given Dr. Hilbert bandage surgery

• $P(A|B) > P(A|B^c)$
  : success given Dr. Nick's surgery > success given Dr. Hilbert surgery (fliped!)

• C is a "confounder(통제자)"

  • cf. 확률에서의 confounder

Law Of Total Probability approach

• Basic argument : $P(A|B) = P(A|B, C)P(C|B) + P(A|B, C^c)P(C^c|B)$

  • $P(C|B)$ (heart surgery by Dr. Nick) and $P(C^c|B)$ (bandage surgery by Dr. Nick) would like weights to multiply $P(A|B, C)$ and $P(A|B, C^c)$

  • $P(A|B, C) < P(A|B^c, C)$, $P(A|B, C^c) < P(A|B^c, C^c)$
    : compared by Dr. Hilbert (Dr. Nick < Dr.Hilbert)

  • The weights are quitely different for each terms,
    so it can't prove that Simpson's Paradox is not right

• 출처 : Statistics 110, boostcourse