Lecture 5: Conditioning Continued, Law of Total Probability

Thinking

• Thinking conditionally is condition for thinking!

• How to solve a problem

  1. Try simple and extreme cases
  2. Break up problem into simpler pieces.
     : Let $A_1 \; ... \;A_n$ partition of S
     $P(B) = P(B \cap A_1) + \; ... \; + P(B \cap A_n)$
     $= P(B|A_1)P(A_1) + \; ... \; + P(B|A_n)P(A_n)$

  

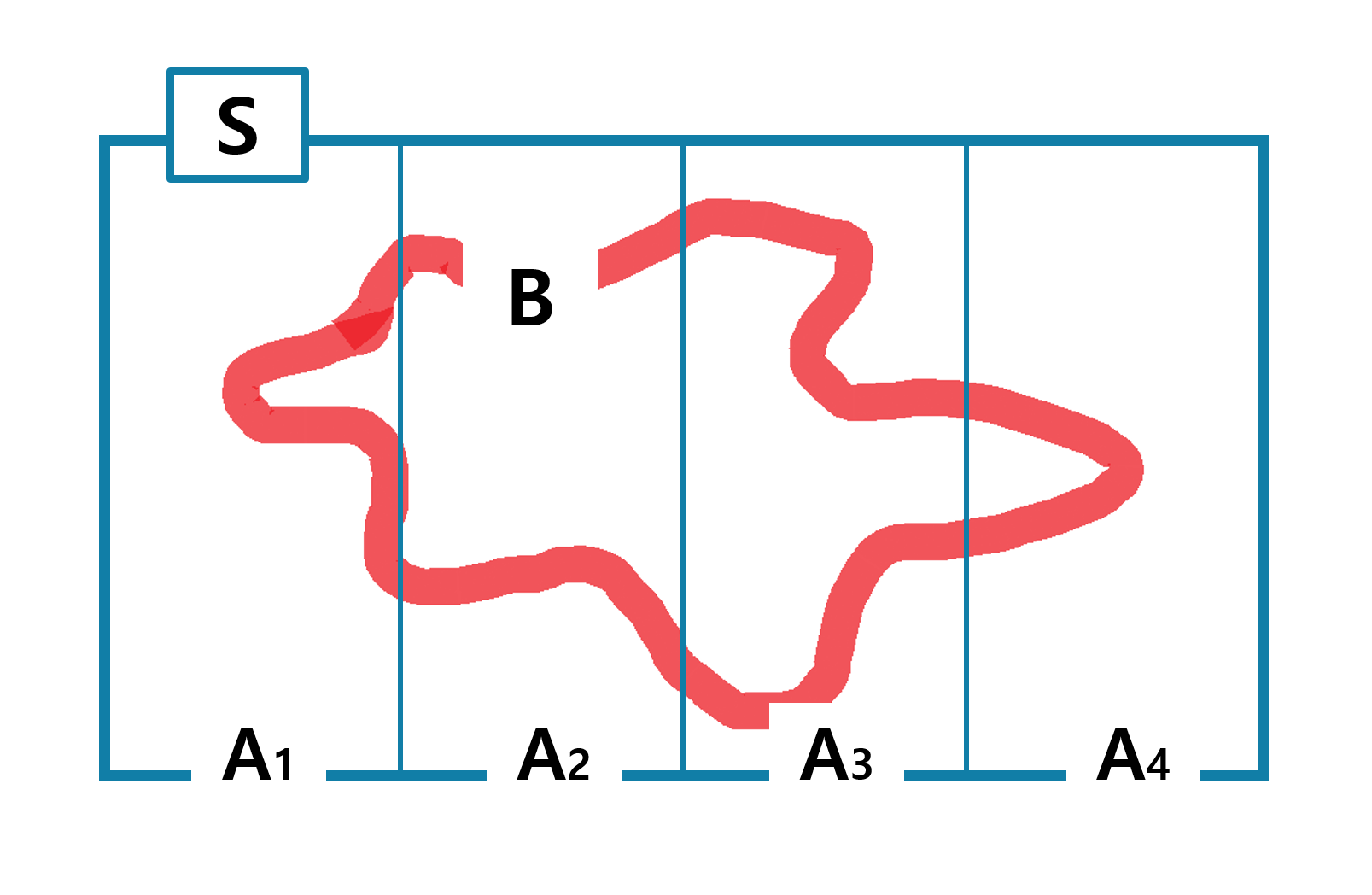
• Ex1. get random 2-card hand; from standard deck

  Find $P(both aces|have ace), P(both \; aces|have \; Ace \; of \; Space)$

  • $P(both \; aces|have \; ace)= \frac{P(both \;aces, ~~have \;ace~~)}{P(have \;ace)} = \frac{\begin{pmatrix}4\\2\\ \end{pmatrix}/\begin{pmatrix}52\\2\\ \end{pmatrix}}{1-\begin{pmatrix}48\\2\\ \end{pmatrix}/\begin{pmatrix}52\\2\\ \end{pmatrix}} = \frac{1}{33}$

  • $P(both \; aces|have \; Ace \; of \; Space) = \frac{3}{51} = \frac{1}{17}$
    : | AS | | ? |

  • 한 장의 ACE를 이미 뽑은 경우라면, 그 다음 카드를 뽑는 순간에 ACE를 뽑을 확률은 첫 확률보다 2배 크다.

• Ex2. Patient gets tested for disease afflicts 1% of population, tests positive(get disease)

  • Suppose test as advertised as "95% accurate"

    • D: patient has disease, T: patient tests positive

    • suppose this means $P(T|D) = 0.95 = P(T^c | D^c)$

  • $P(D|T) = \frac{P(T|D)P(D)}{P(T)} = \frac{P(T|D)P(D)}{P(T|D)P(D) + P(T|D^C)P(D^c)} \approx 0.16$

    • Using Bayes's rule : $P(D|T) = \frac{P(T|D)P(D)}{P(T)}$
    • Intuition
      : 1000 occations, about 10 of them have the disease (990 have not) 실제 질병이 존재하는 사람 수

    : According to accuracy, 50 people(5% of them) get tested positive. 전체 tester 중에 양성 반응을 보인 사람 수

    : so, the ratio of this is too small, 10/50 approximately 0.2.

  • cf. Bayes's rule
    : 어떤 증거를 얻든 전체 사건의 조합에 해당하므로, lunch를 먹기 전에 관찰하든, lunch를 먹고 난 후에 관찰하든 상관없다!

    -> 관심 있는 한 사건에 언제든지 focusing 해도 좋다는 장점을 지님.
    

Biohazards

1. confusing $P(A|B), P(B|A)$ ("prosecutor's fallacy")

   • Ex. Sally Clack case, SIDS(영아 돌연사 증후근).

     • 자연사 확률

       $\frac{1}{8500} * \frac{1}{8500} = \frac{1}{73 \times 10^6}$

       : $\frac{1}{8500}$ But second term assumes independent.

     • want $P(innocent|evidence)$

       : most of mother did not kill their children, so before this occation,
       innocent prob. is almost 1. -> This was completely ignored!

2. confusing $P(A)$ "prior(사전)" with $P(A|B)$ "posterior(사후)".

   • $P(A) = 1$과 $P(A|A) = 1$는 다른 의미다.

3. confusing independence with conditional independence.

   • Defn. Events A, B are conditionally indep. given C

     • if $P(A \cap B|C) = P(A|C)P(B|C)$

     • Does conditionally indep. given C imply indep. ? No!

       Ex. chess opponent of unknown strength.
       : may be that game outcomes are conditionally indep. given strength of opponent, but not indep.

       : 상대에 따라 달라지는 것이므로 무조건적인 독립이 아니라 조건부 독립이다.

     • Does independence imply conditional indep. given C? No!

       Ex. A : fire alarm goes off. (울리게 한다.)
       caused by F : fire, C : popcorn

       suppose F, C indep. But $P(F|A, C^c) = 1$ -> not cond. indep. given A

       : 팝콘을 튀기는 사람이 없는데도 화재 경보기가 울렸다면 더 이상 indep.가 아니다.

• 출처 : Statistics 110, boostcourse