벡터와 공간 | 차원

Dimension : Null space or Nullity

• If you have a matrix B, let's get the Null space of B.
  • You've got right now that the vectors are in a 5 dimension of real space.

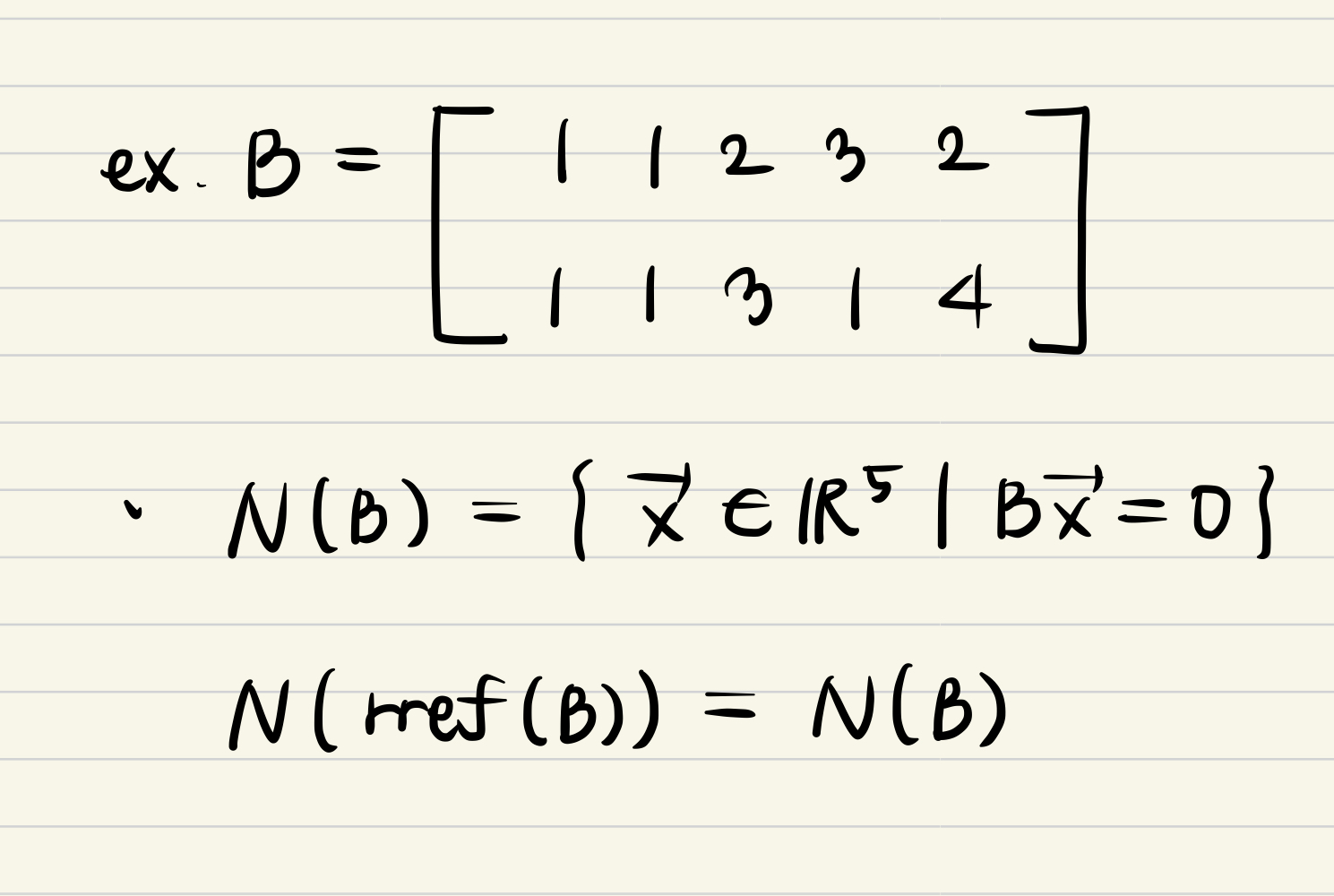
• And we already know about the Null space of B is equal to Null space of rref(B)
  • Then you can find pivot values, and free values in that form, the last we have to do is that represent the pivot variables by using linear combination of free variables.

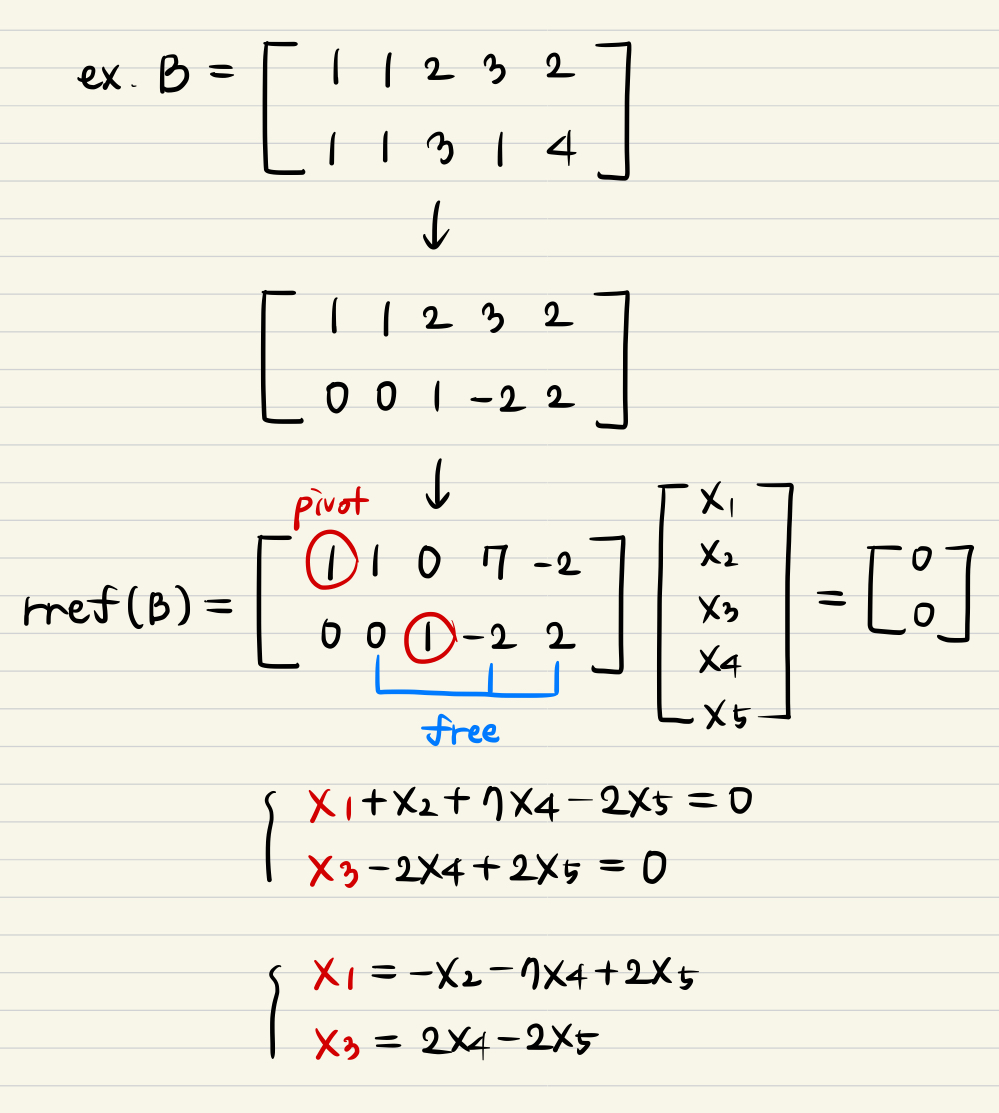
• When you represent the solution of vector x to linear combination of free variables, there are three vectors v1, v2 and v3 that you could get.

  • It contains like 100, 010, 001, which means one of them can not be represented to linear combi. of the other vectors.
  • In other words, there are Linearly Independent!!

• The conclusion is that some columns with the free variables(v1, v2, v3) are basis for N(B), same as N(rref(B)), and we can Span the whole space by using that three vectors v1, v2, v3.

  • Because these are the basis!

• Let's define 'Dimension' and 'Nullity'.
  • Dimension is number of elements in a basis for the subspace.
  • Nullity is related to non-pivot columns (free variables).

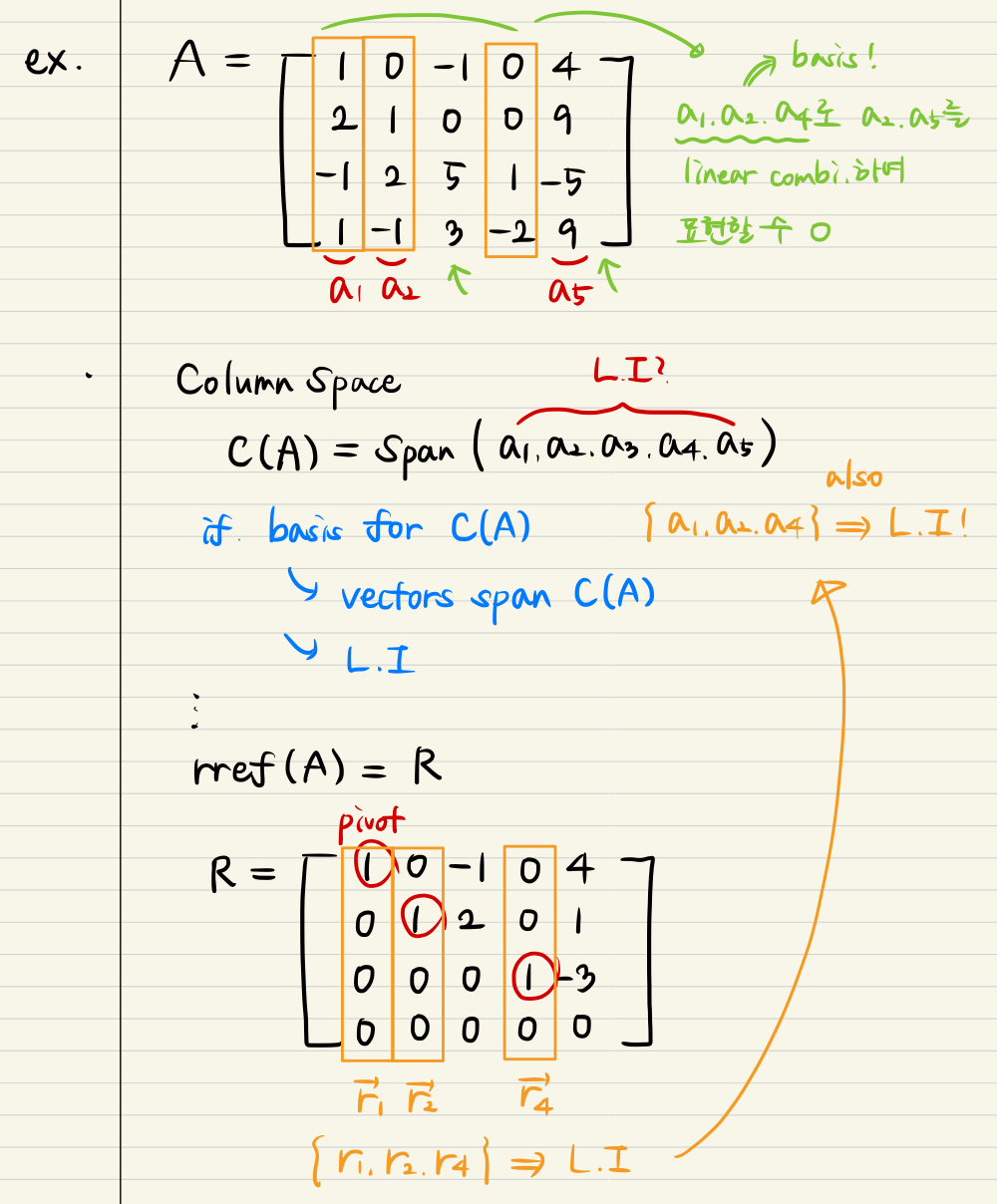
Dimension of the column space or rank

• There is the same way to get dimension of Null space.
  1. Figure out rref(A).
  2. Find pivots and frees.

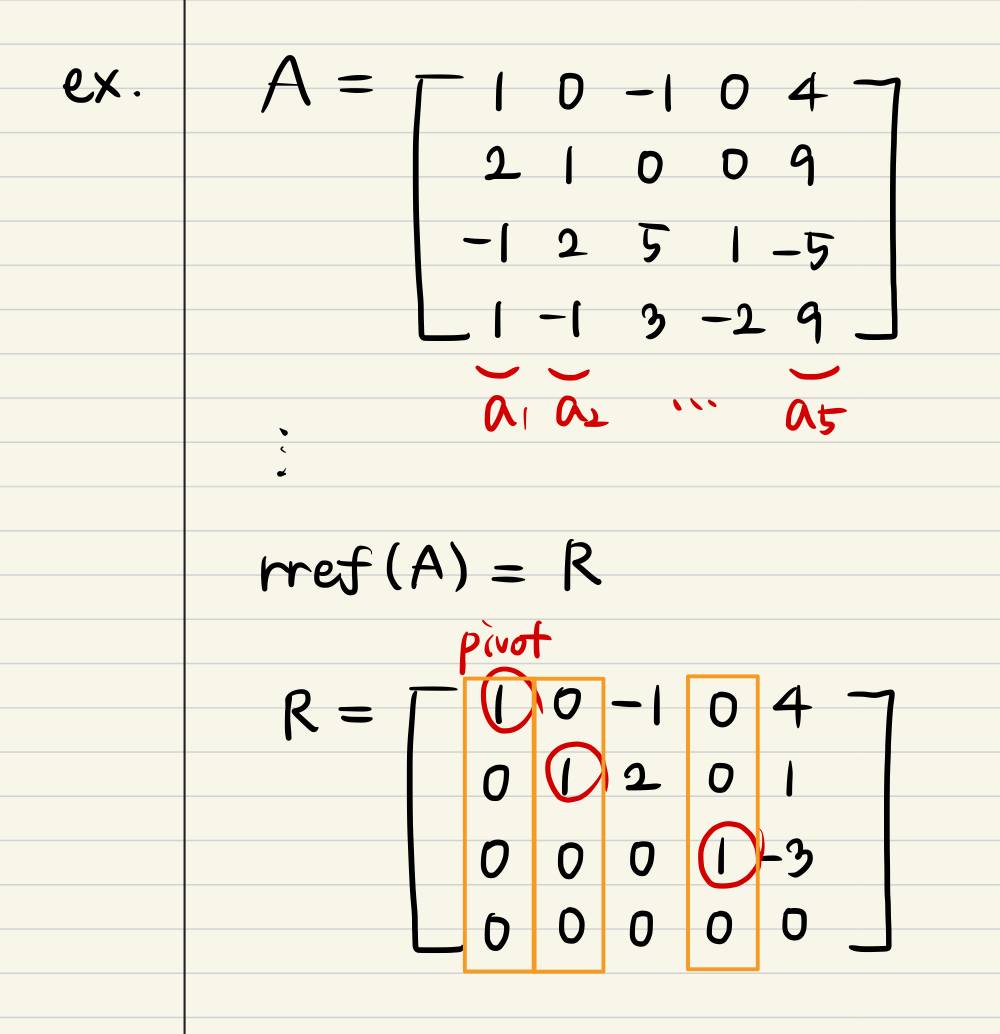
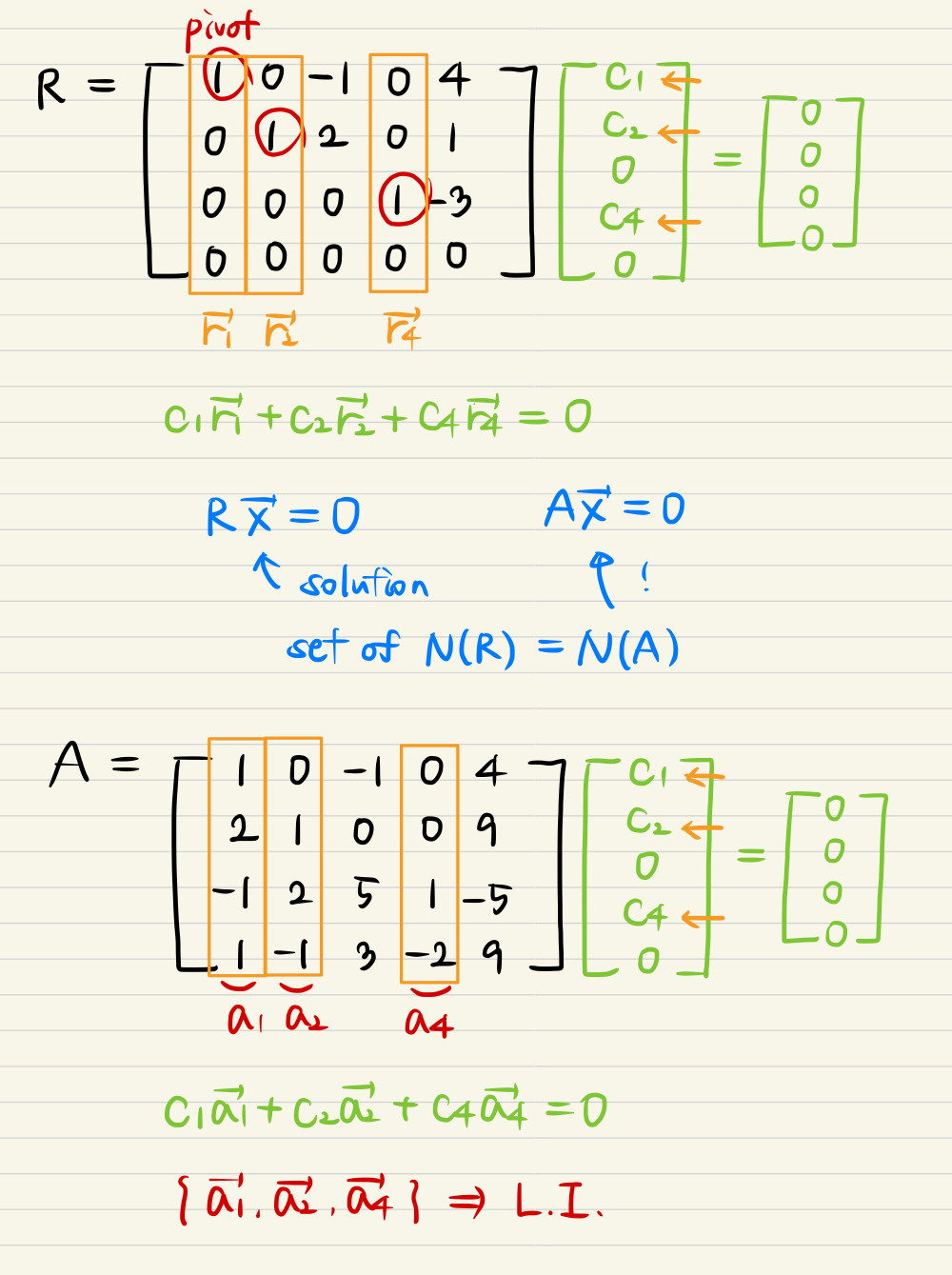
• The pivot columns of R, which is rref(A), and also same position columns of A are Linearly Independent vectors!
  • It means that vectors which is like r1, r2, r4 and a1, a2, a4 are the basis for C(A).
  • Then we can span the whole space by the pivot column vectors.

• The conclusion is symmetric way of defining Dim of Null space and Nullity.
  • The one thing we have to change is Null space to Column space.
  • And non-pivots to pivots!

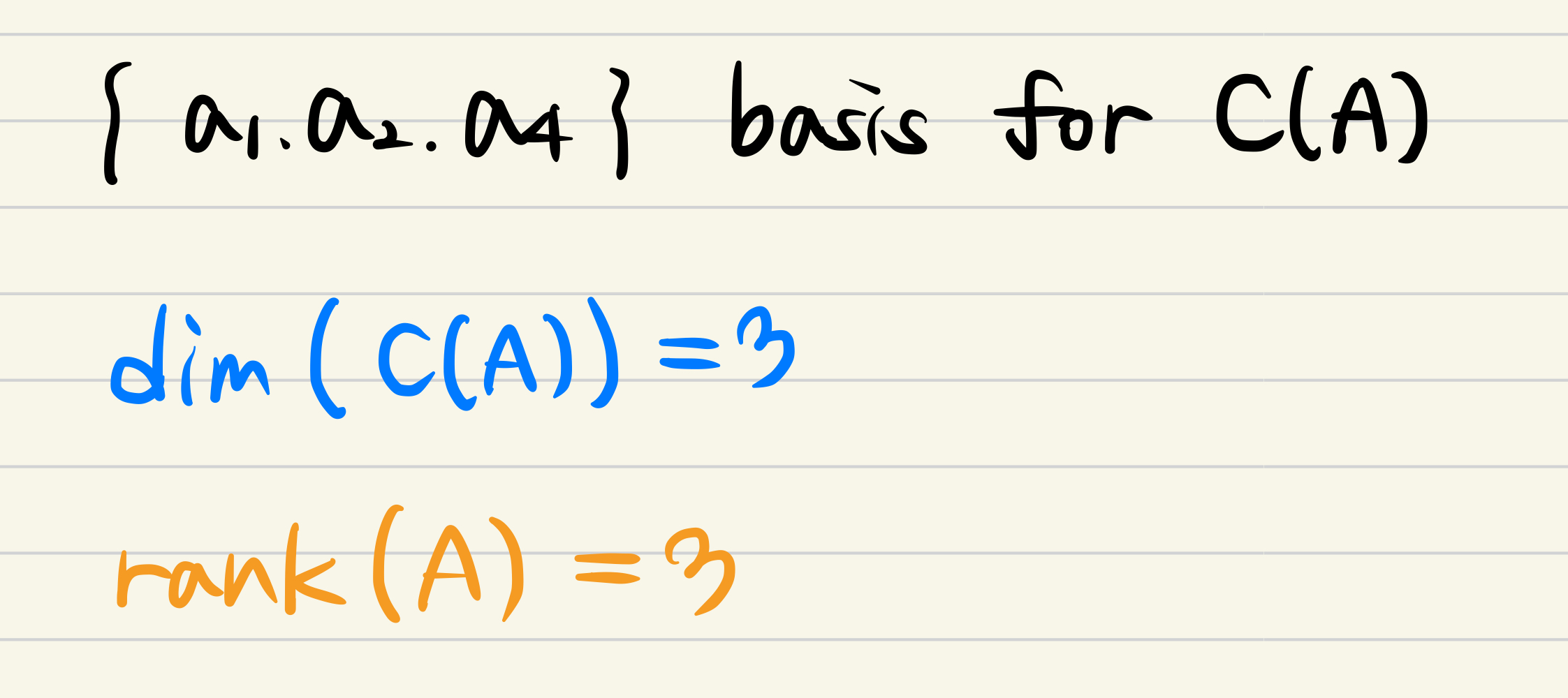
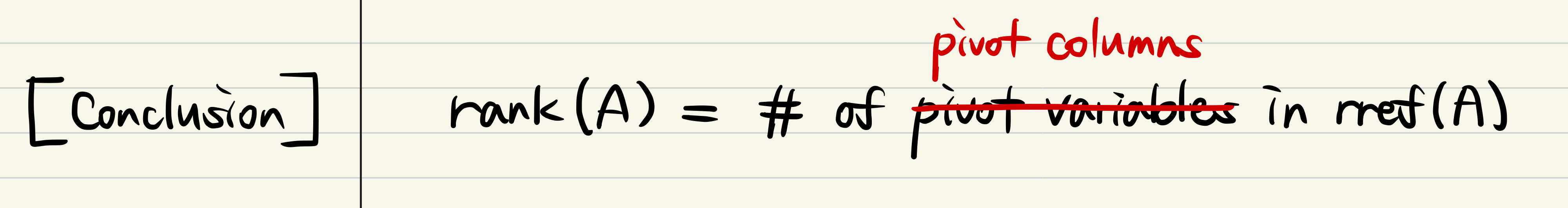
Showing relation between basis cols and pivot cols

• In general, set of pivot columns for any rref matrix is Linearly Independent!!
  • It means there is the only solution that linear combination of pivots equal to 0.
  • All the constants times with the pivots are 0!

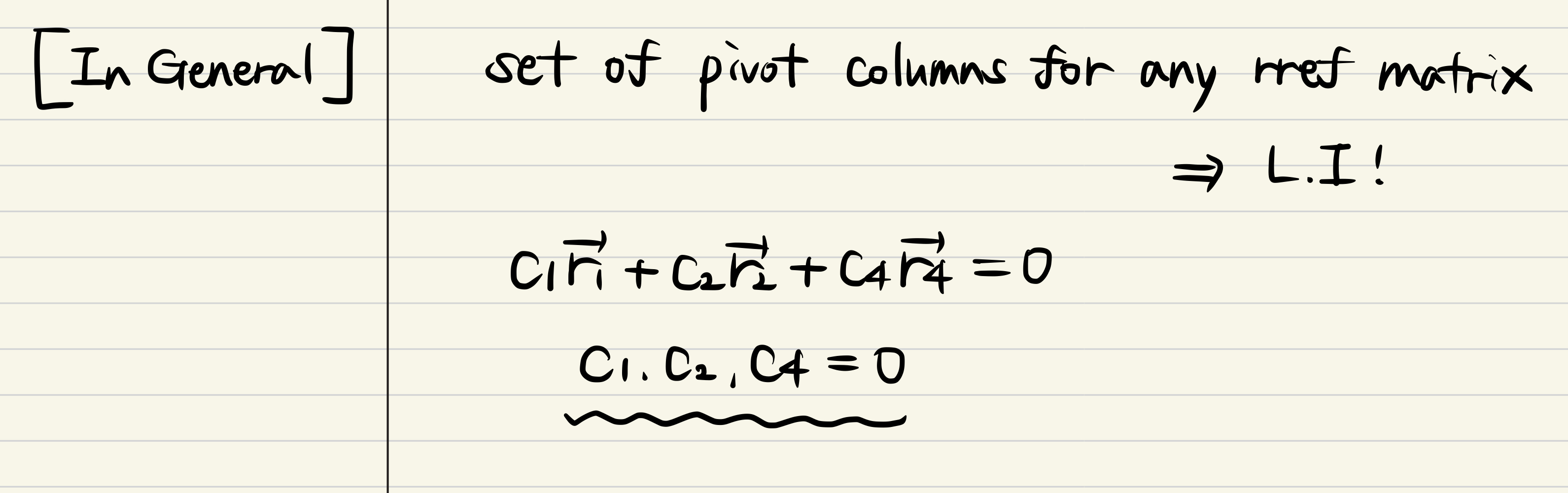
• Obviously, when you find out the pivot columns of R, because N(R) is equal to N(A), Null space A should be had the pivots at the same position.
  • Then the pivots of R and same pos. of A are the linearly independent set.

Showing that the candidate basis does span C(A)

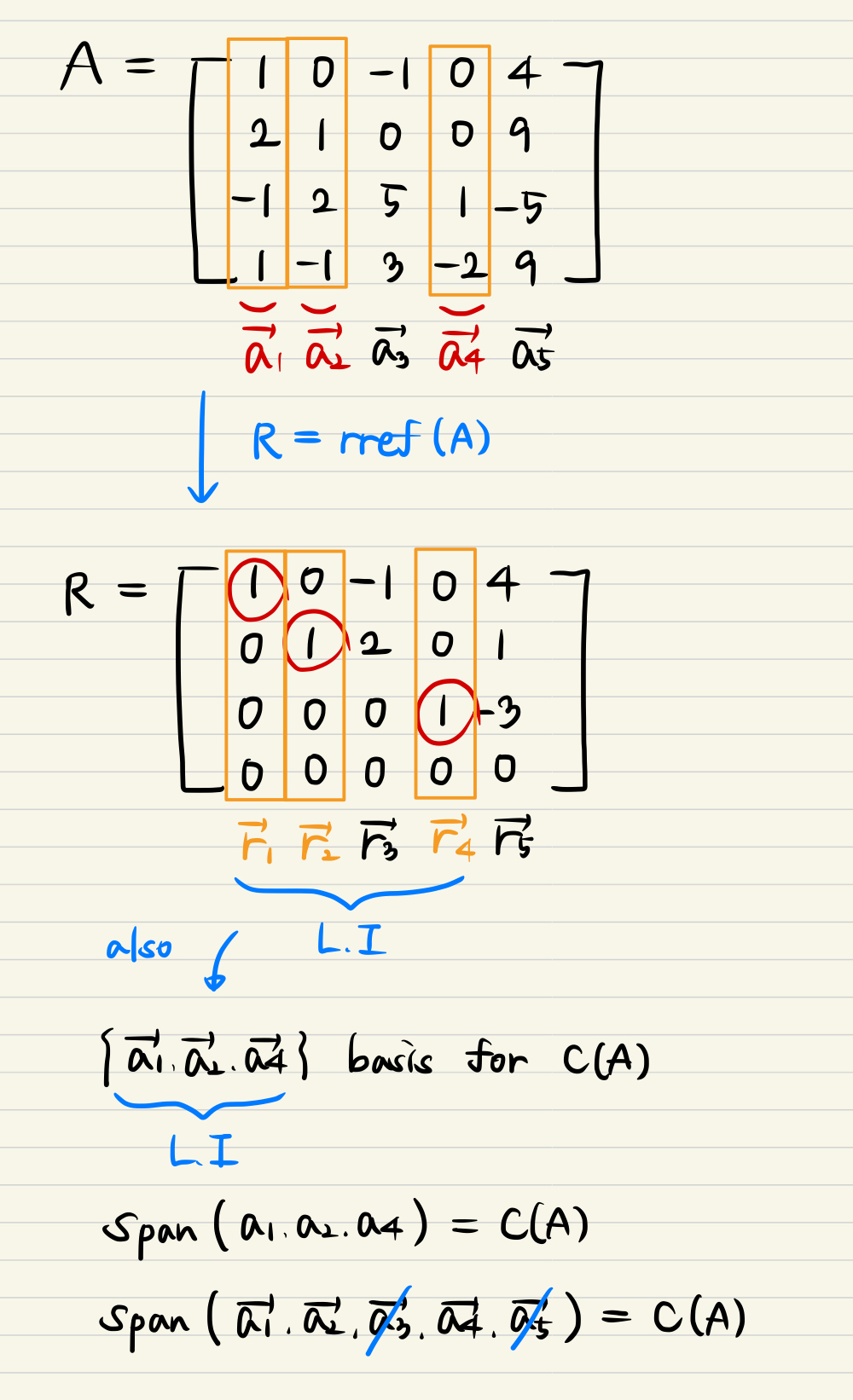
• Let's rewrite the basis for Column space of A, one last time.
  • a1, a2, a4 are the basis set of using span the whole space and also linearly independent.
  • Which means a3 and a5 is not necessary for spanning the space!

• The one thing we have to remind is that the free variables, which is not pivots, can be represented by using the pivot variables.
  • Generally, set one of the value of frees is equal to -1, and the rest of it to 0.
  • Because there are 'free' variables that you can set to anything you want!