벡터와 공간 | 열공간

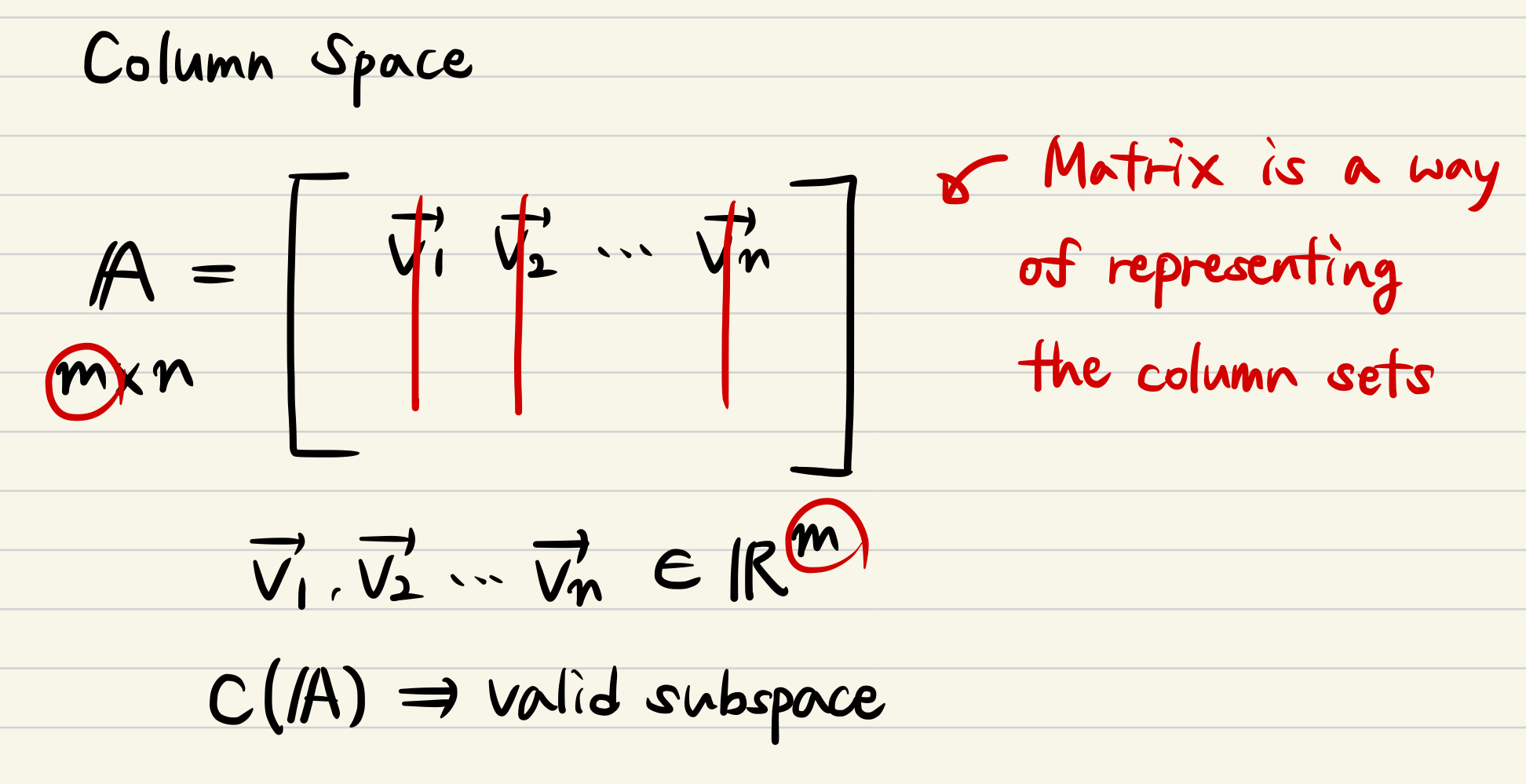
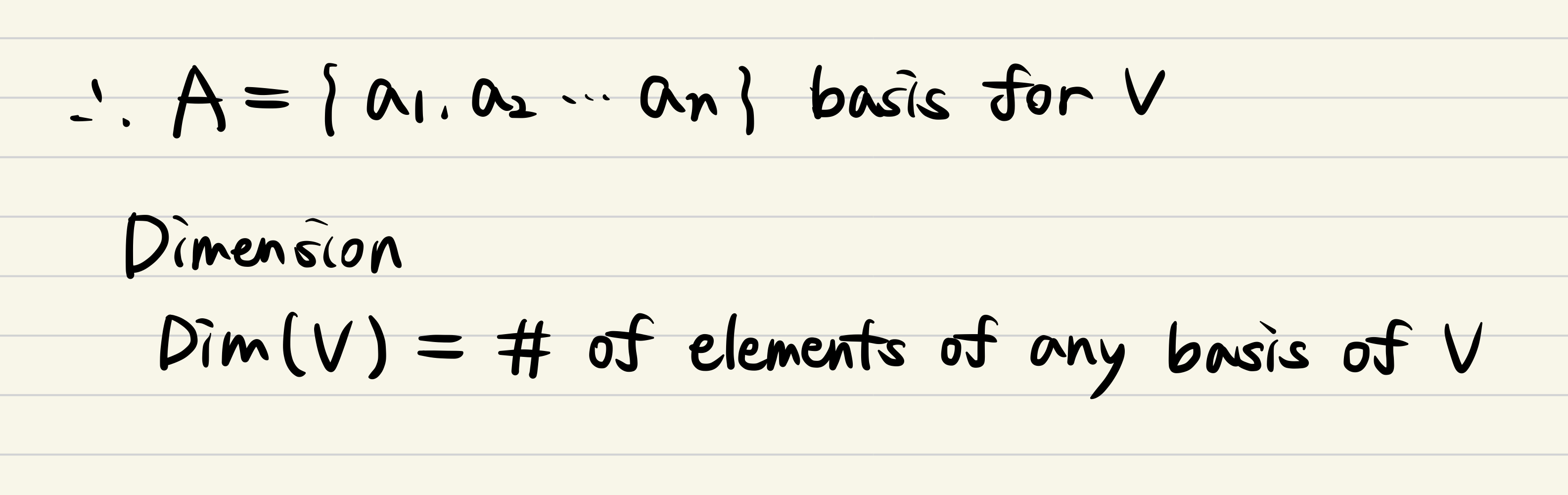Column space of a matrix

• What is the column space?
  • If you have the matrix A which size is m by n, you can span the subspace by using n vectors of column sets.
  • Matrix is the just a way of representing the column sets.

• If you get the column space of matrix A, which has spanned for column vectors, linear combination & multiplication of element vectors is also in the column space.

• If you have a linear combination of column vectors of A, you can span the space of columns and also find out the solution of x components.

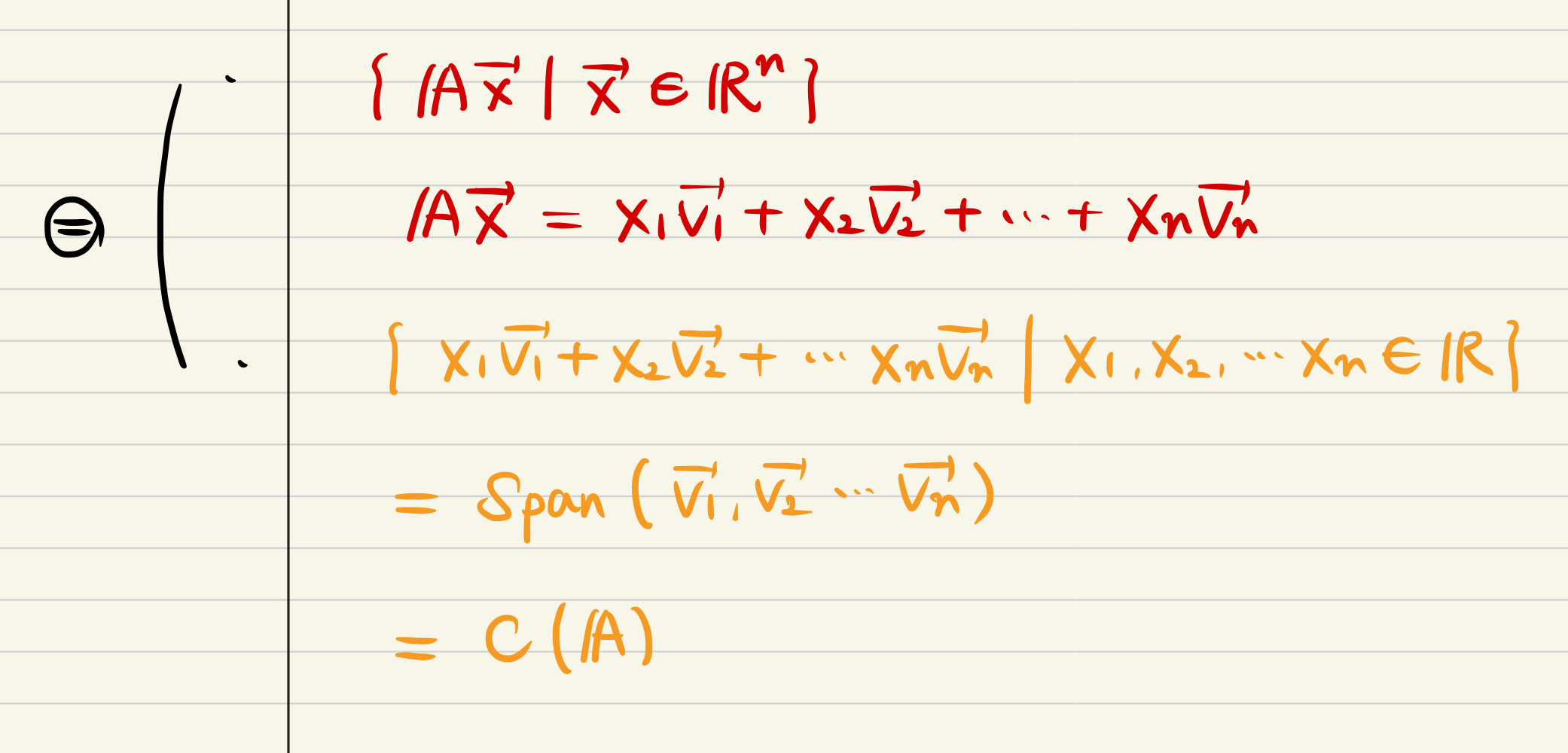
• There are two ways of solution.
  1. If b1 is not in the column space of A. Ax = b1 has no solution.
  2. If b2 has at least 1 solution, b2 is in the column space of A.

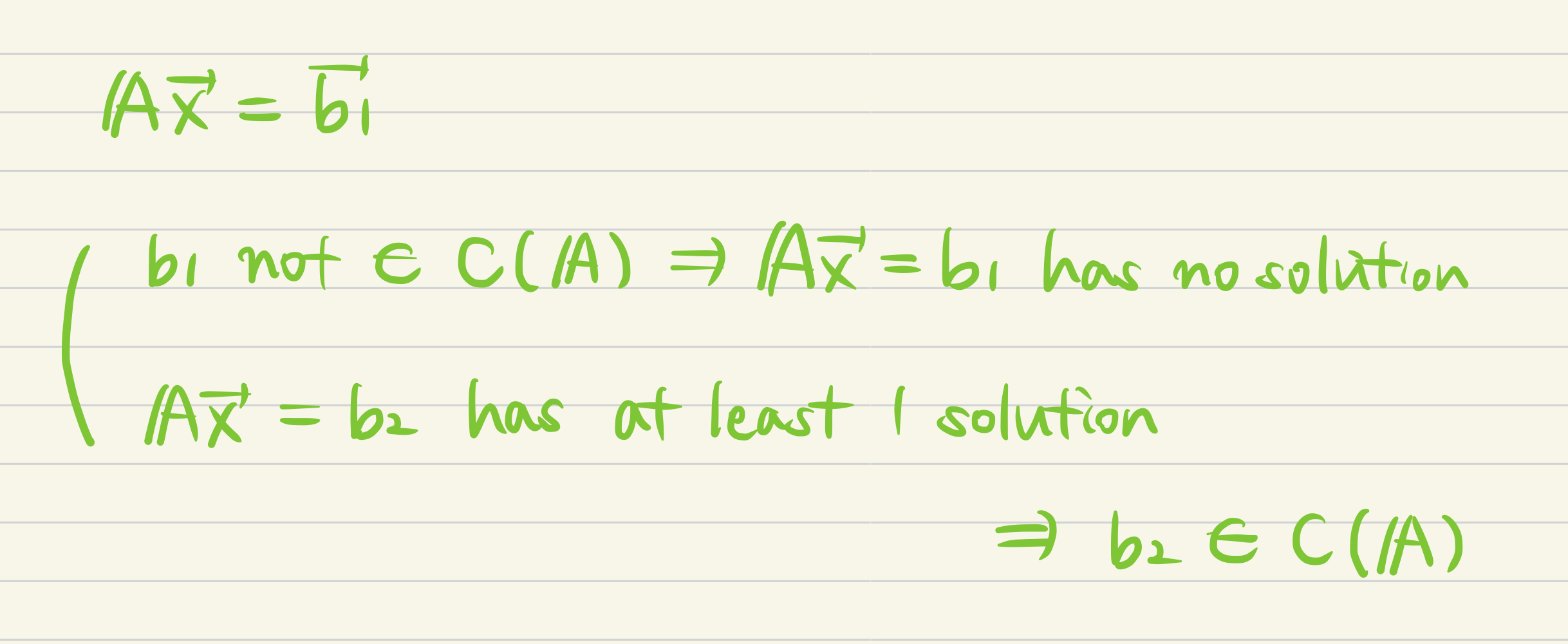
Nullspace and column space basis

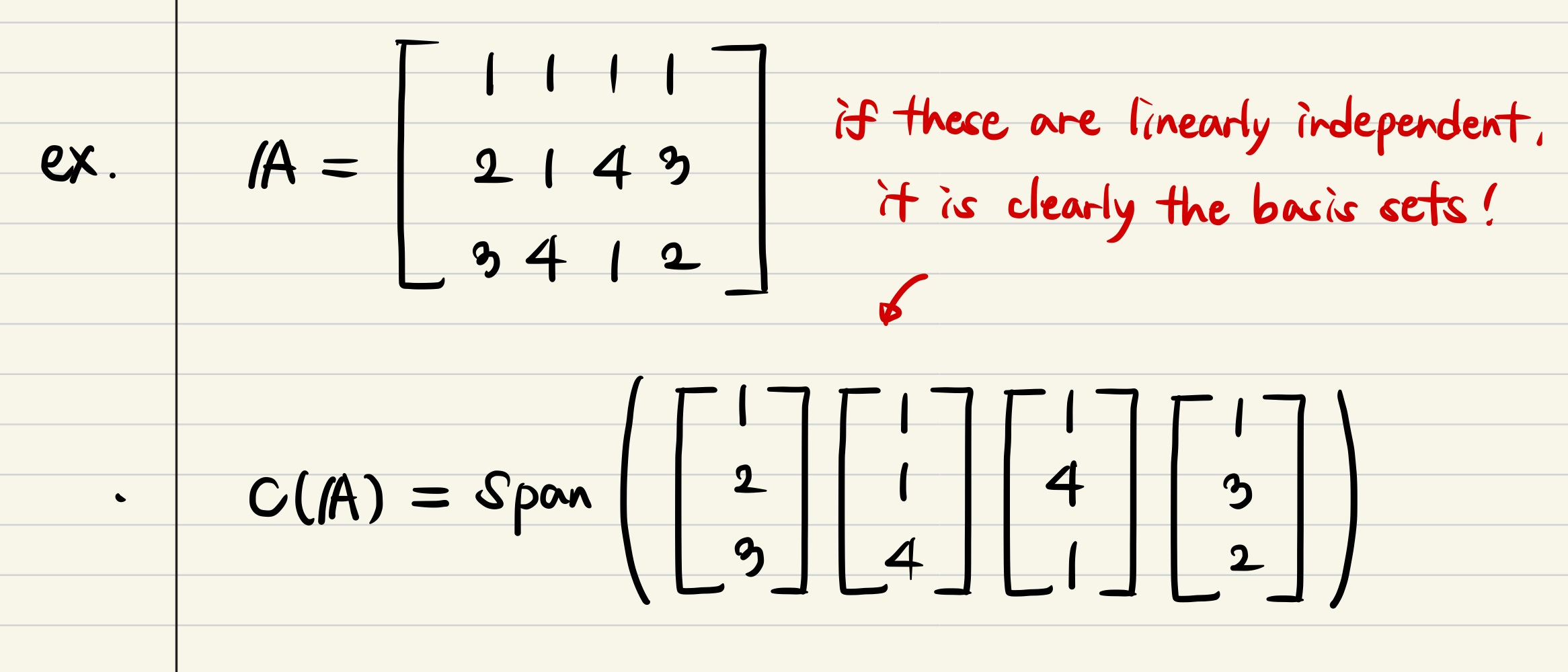
• For example if you have a matrix of A, you can easily span the column space represented by column vectors.
  • # of column sets just can be comprehensed by matrix's width.
  • If these are linearly independent, it's clearly the basis sets.

• Here is the way to find out the basis of Null space.
  • We can figure it out by Null space of matrix A, especially Null space of rref A.
  • Then we can distinguish which is the pivot value, and also the free variables.
    • In this case, x1 & x2 are the pivots, and x3 & x4 are the free variables.

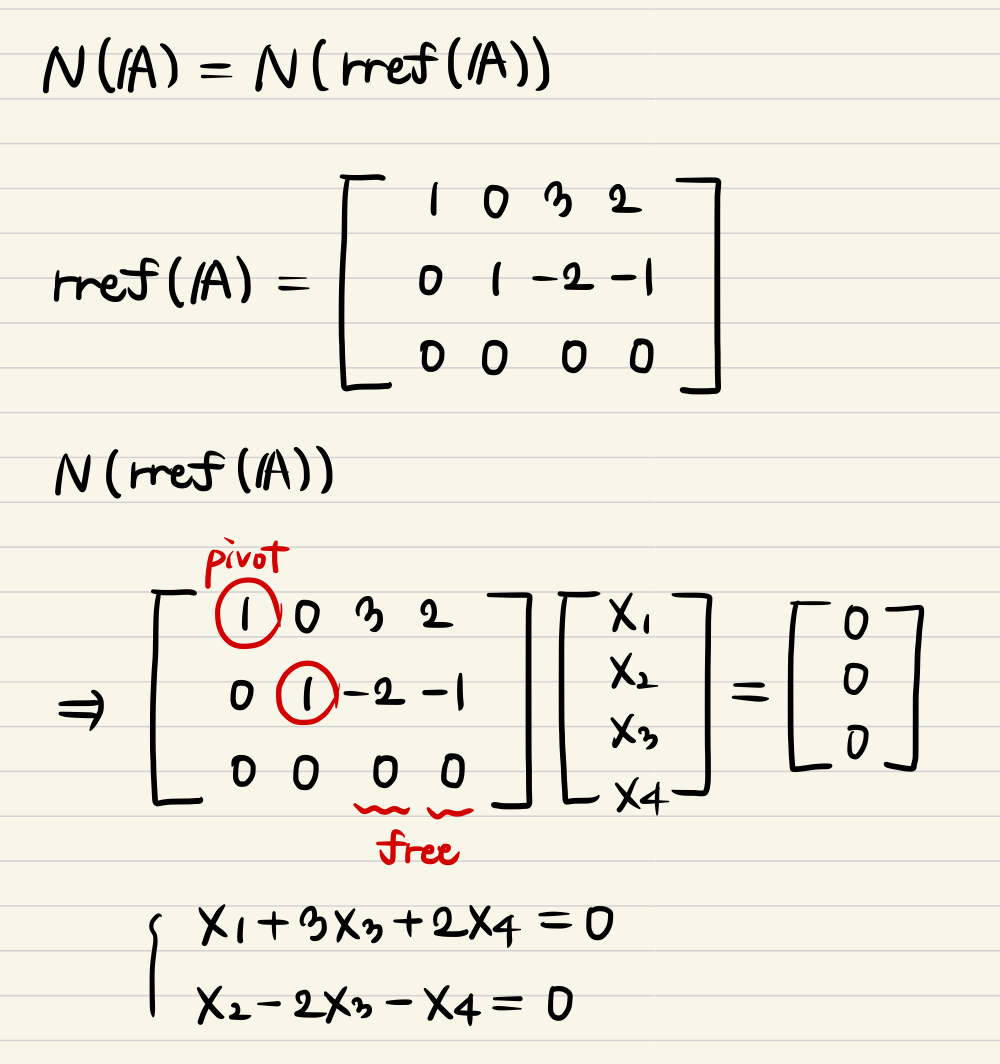
• Null space of spanning rref(A) is very simplified by using that linear combination of free variables of matrix.

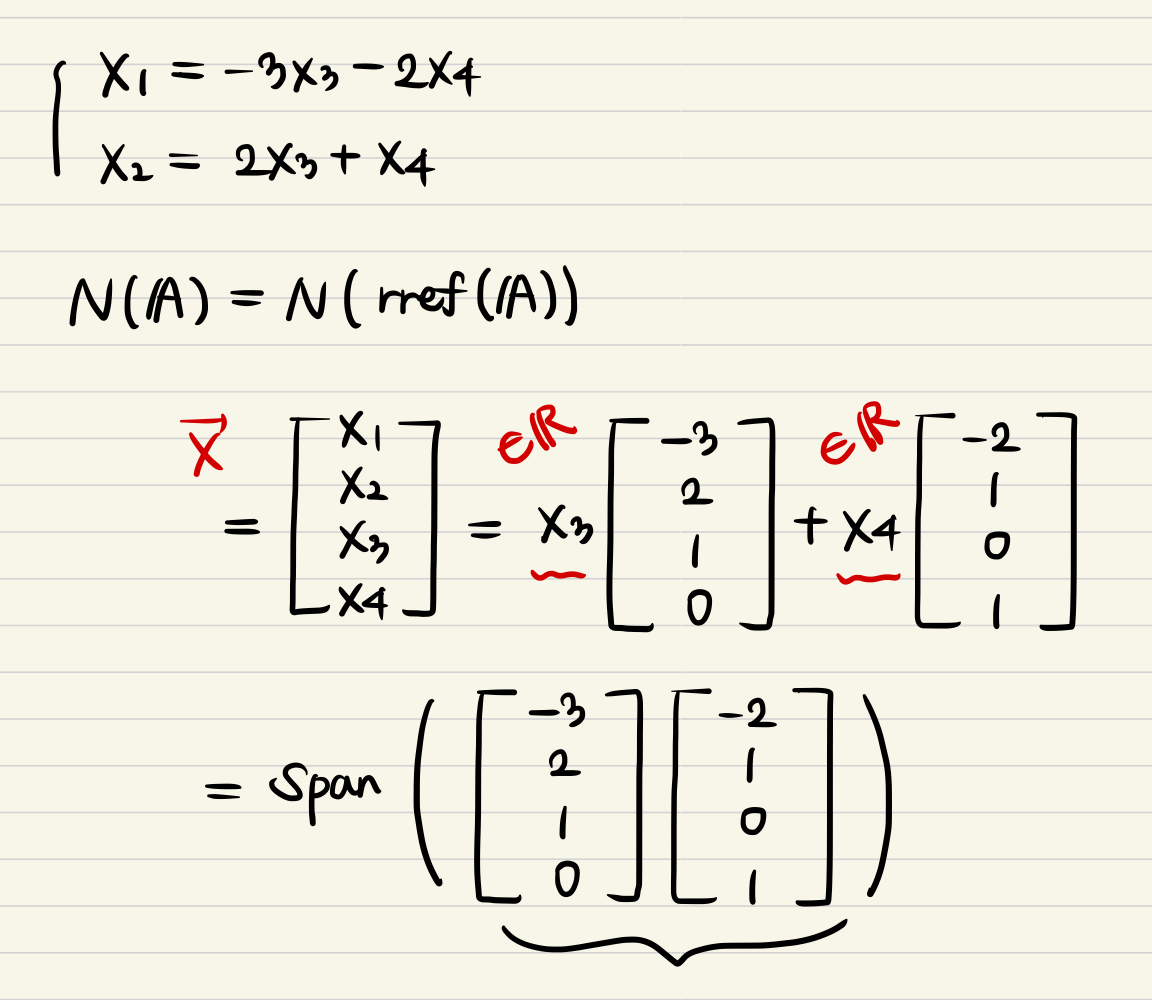
• Then how can we recognize that the matrix is linearly independent or not?
  • If you try to get Null space of matrix, Ax = 0, there is the way to be a linearly independent set.
    → 0 vector must be the only component of the Null space set.
  • If Null space has more sets than just of 0, it is the linearly dependent set.

• Let's see the two examples of Ax = 0.
  • If you set the arbitrary component free variables x3 & x4, you can determine the pivot values x1 & x2 by solving the equation of related pivot and free variables.

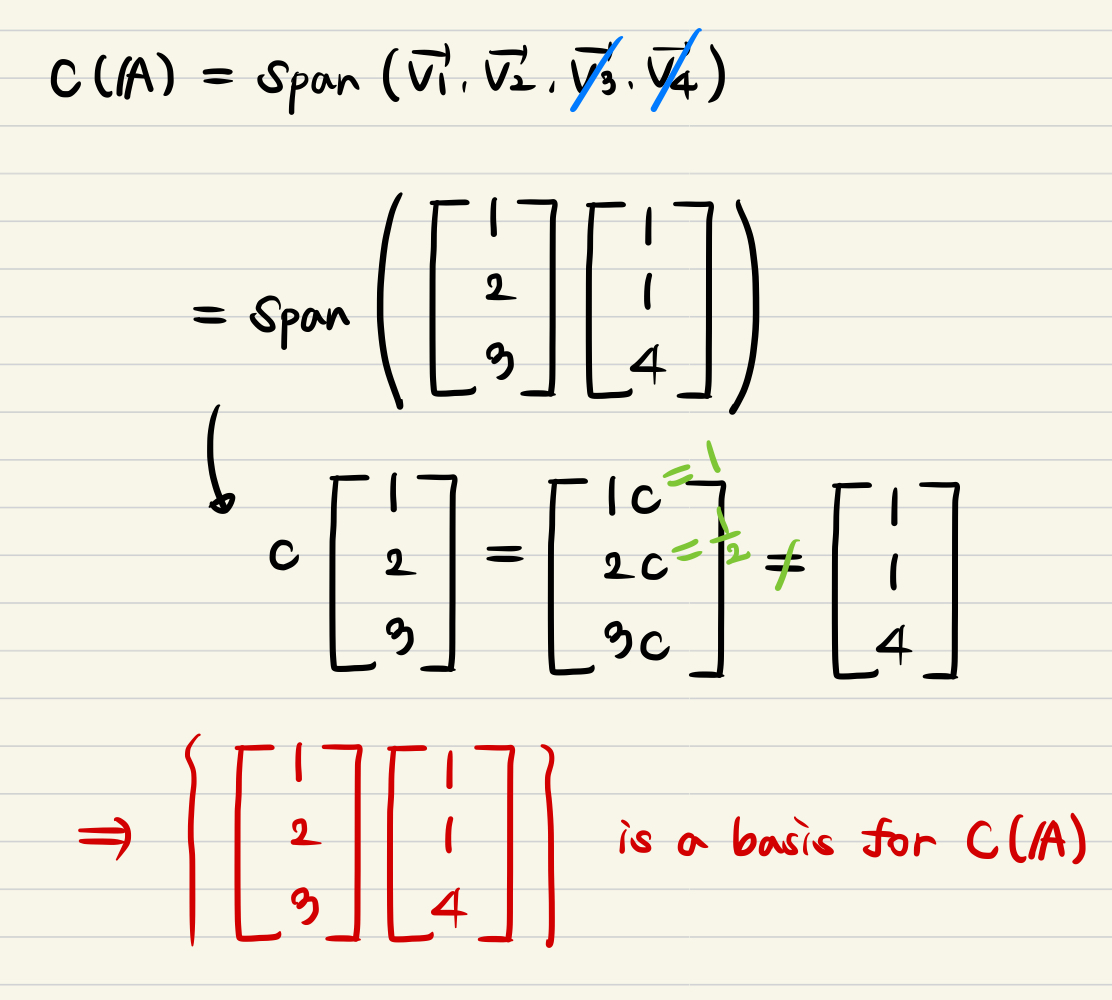
• The conclusion is that a few column vectors can be composed a basis set for column space of matrix A.
  • In this situation, each column vectors which has multiplied by pivot values can be a component of basis set.
  • It means that each column vector can not be represented by a multiplication of other vector.

Visualizing a column space as a plane in R3

• There are two ways of representing the visualization of column space.

  1. By using the normal vector.
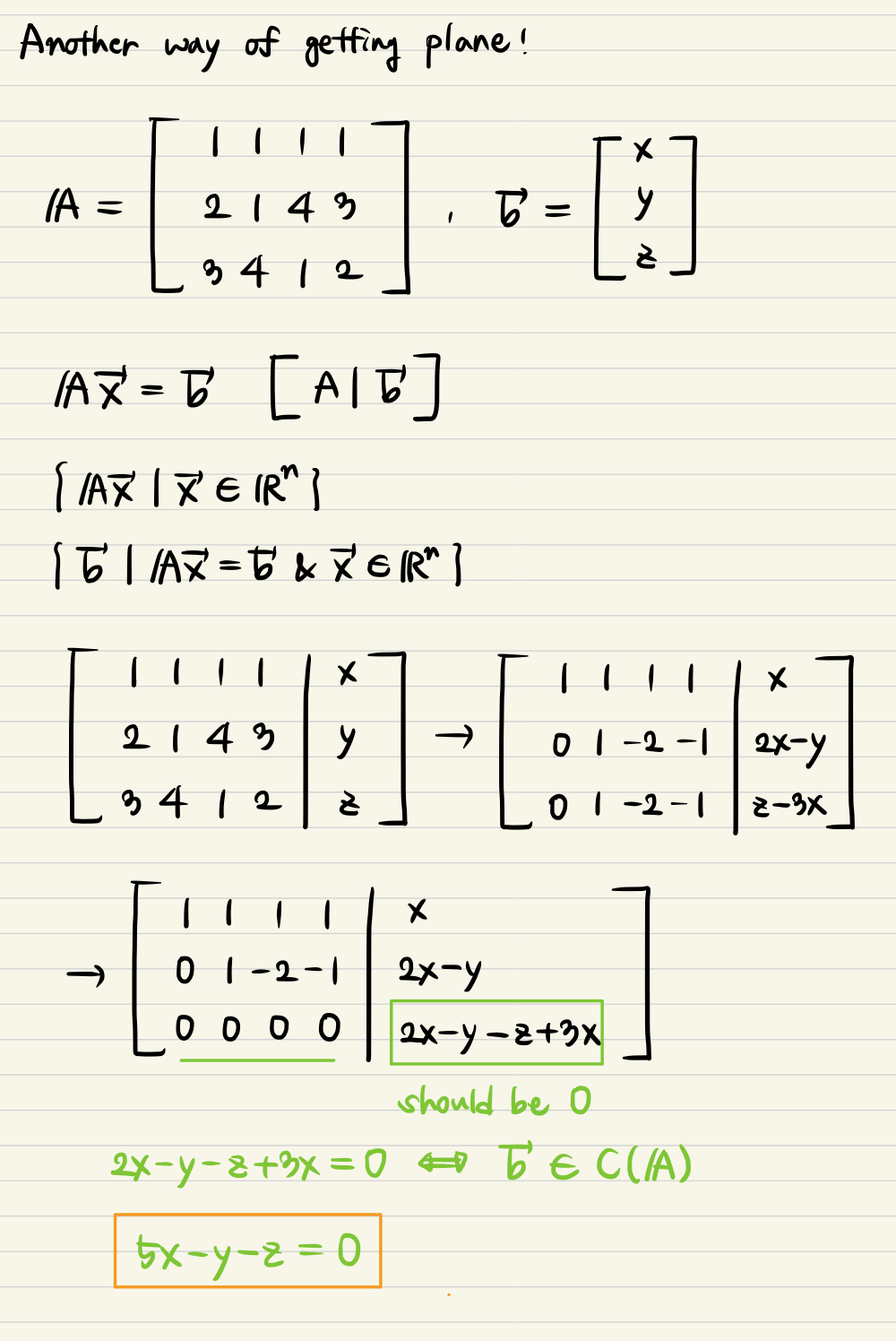
  2. By using rref.

• Calculationg the cross product of basis set, you can take the normal vector from plane.

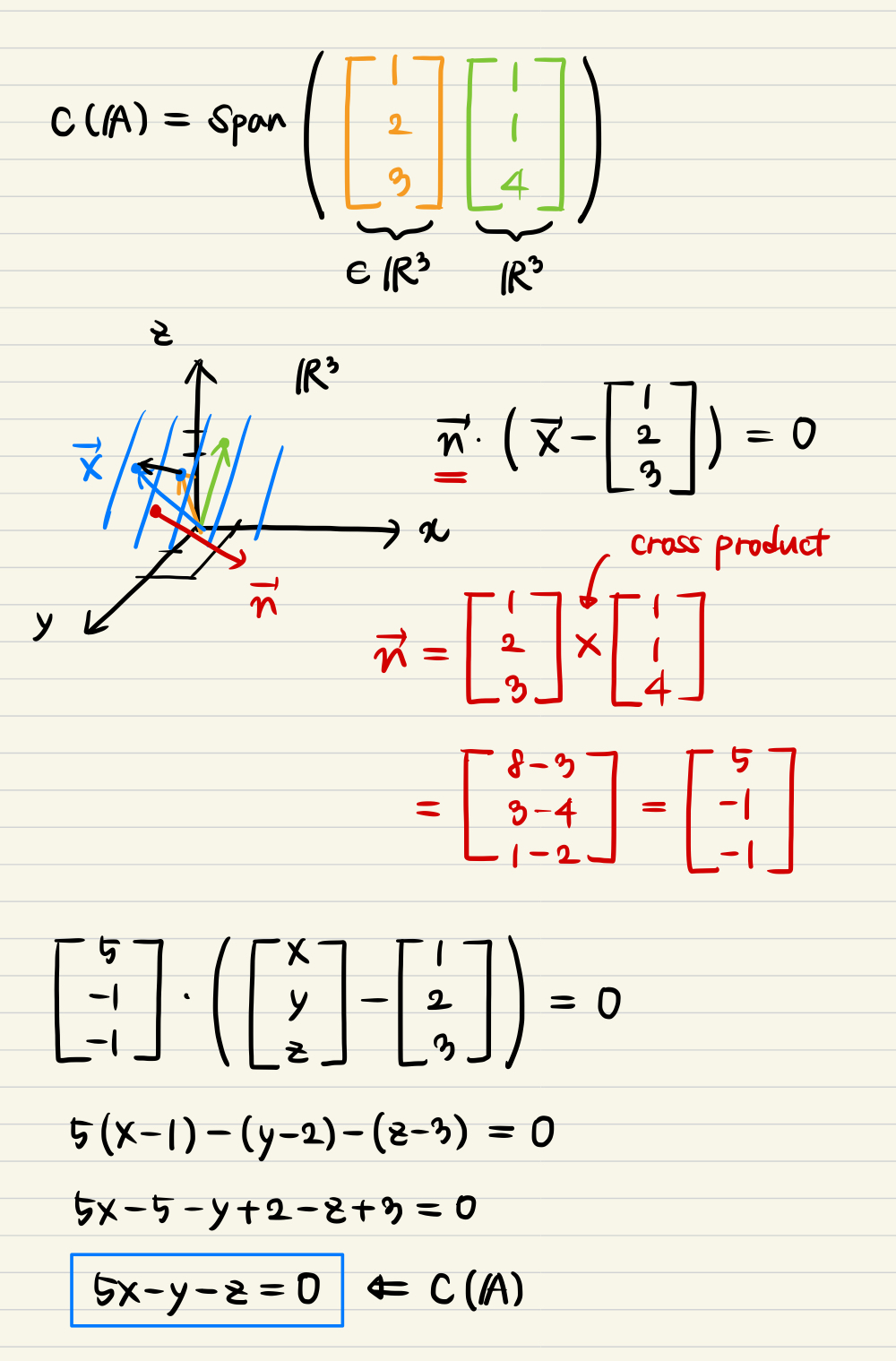
• As you can see, rref could be also used to figure out the plane equation.

Proof : Any subspace basis has same number of elements

• If you get the set(A) as the basis set of span V, which has n components,
  Any spanning set must have at least n-elements.

• Here is the proof by using the set(B) which has m components. (m < n)
  • We will add the elements from A step by step, B1' is the set of not removed dependent component, B1 is the set of removed.

• Step by step..

• You can recognize that set(B) is going to be a subset of A still spanning V.

• The conclusion is that subset A, which is set(B), can not be linearly dependent.
  • Because set(A) is the basis for V which means linearly independent!

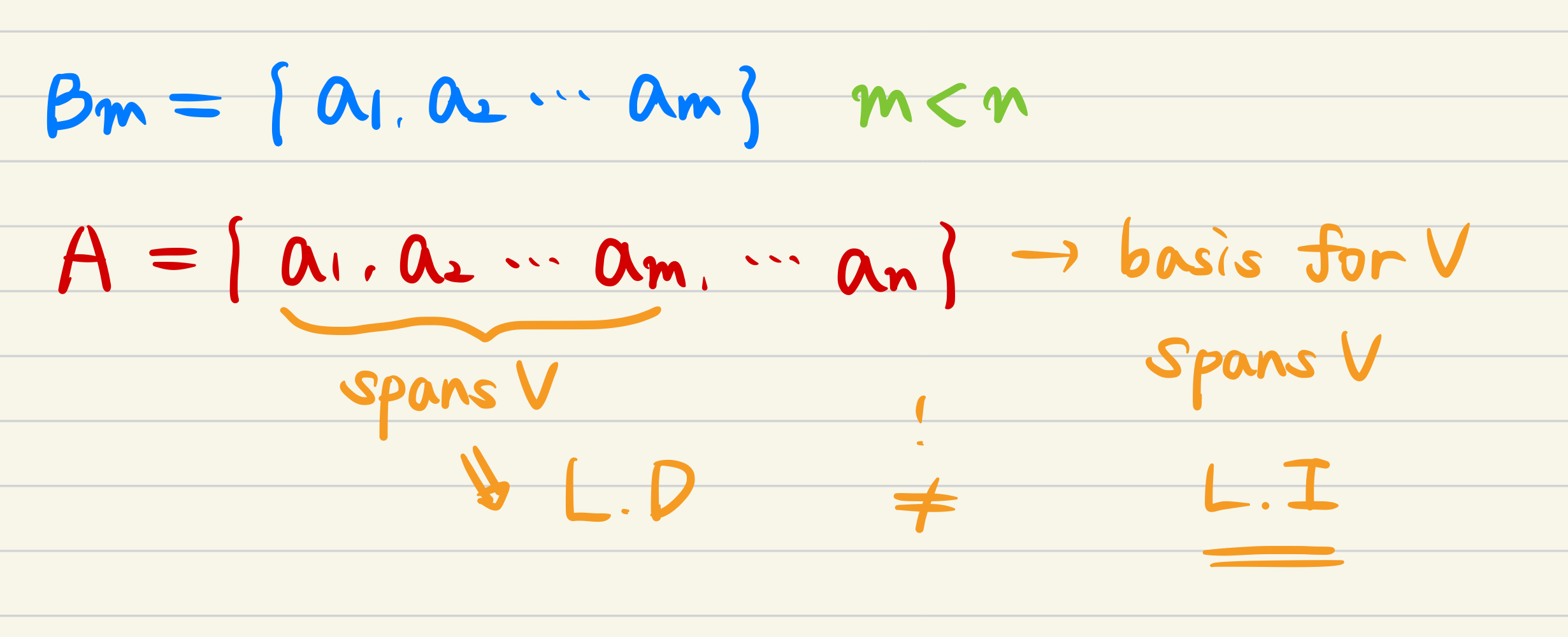
• So, it can not be a spanning set(B) that has fewer elements than set(A).
  • ex. X has 5 components and X is a basis for V, Y is also a basis for V.
    → Y should be have more than 5 components!
• At last, the definition of Dimension appears.
  • It means that number of elements of any basis of V!