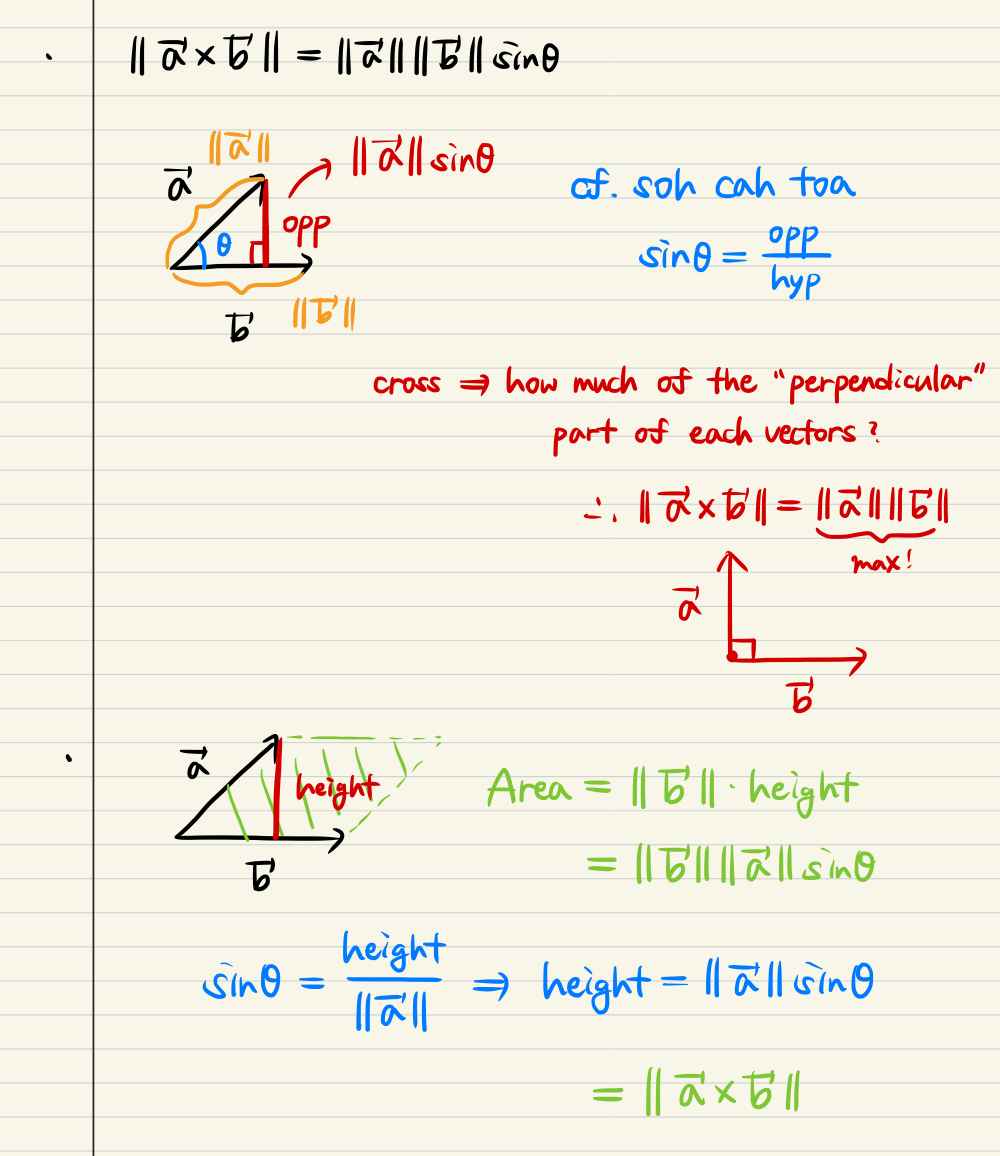벡터와 공간 | 벡터의 외적

Cross product Introduction

• When dot product is a scalar, cross product is a vector which is only defined in R3.
• It's impossible in a R4 or greater!
• The cross product vector of vec a & vec b, is orthogonal to vec a & vec b!
• We can get the direction using for right hand rule!

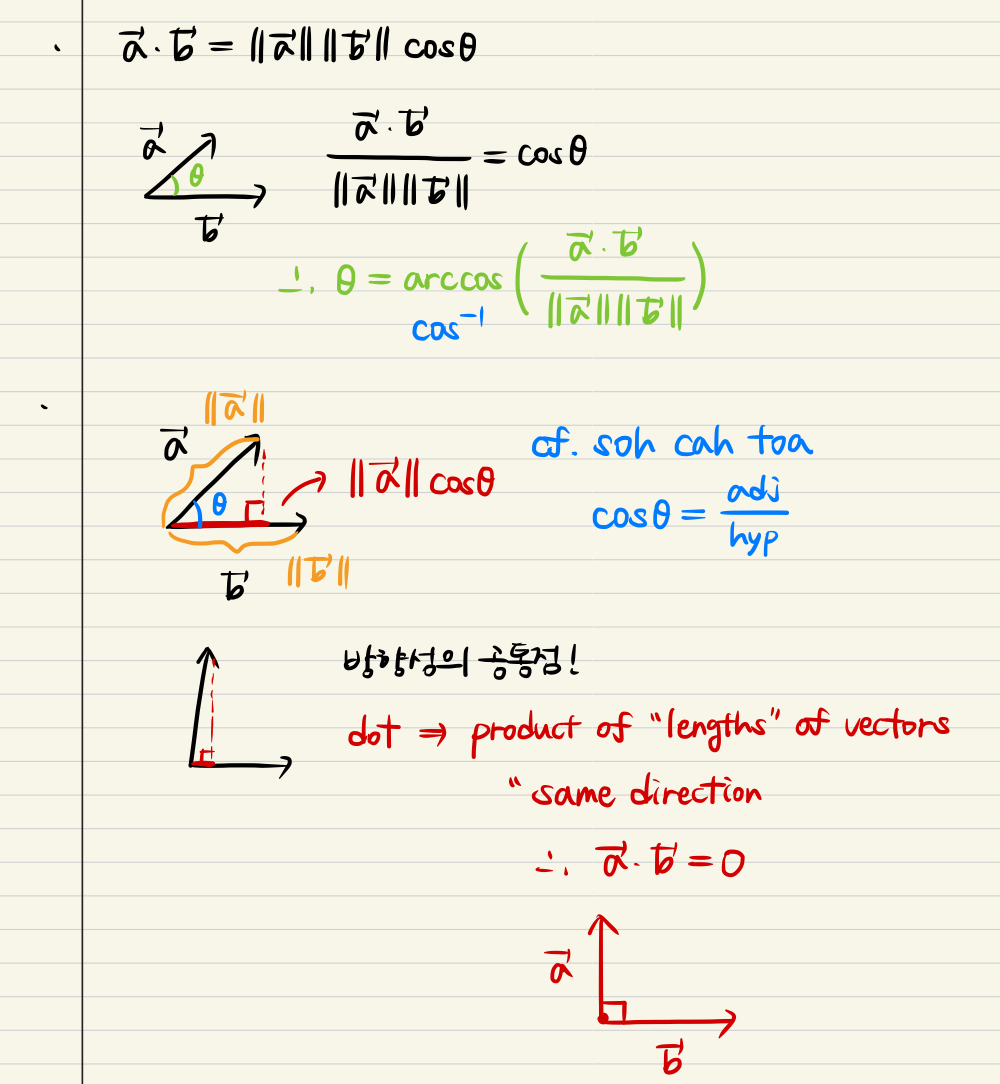
• Orthogonal is a meaning of 0 value of dot product
  • The cross product of vec a and vec b is 0 made for dot a and b

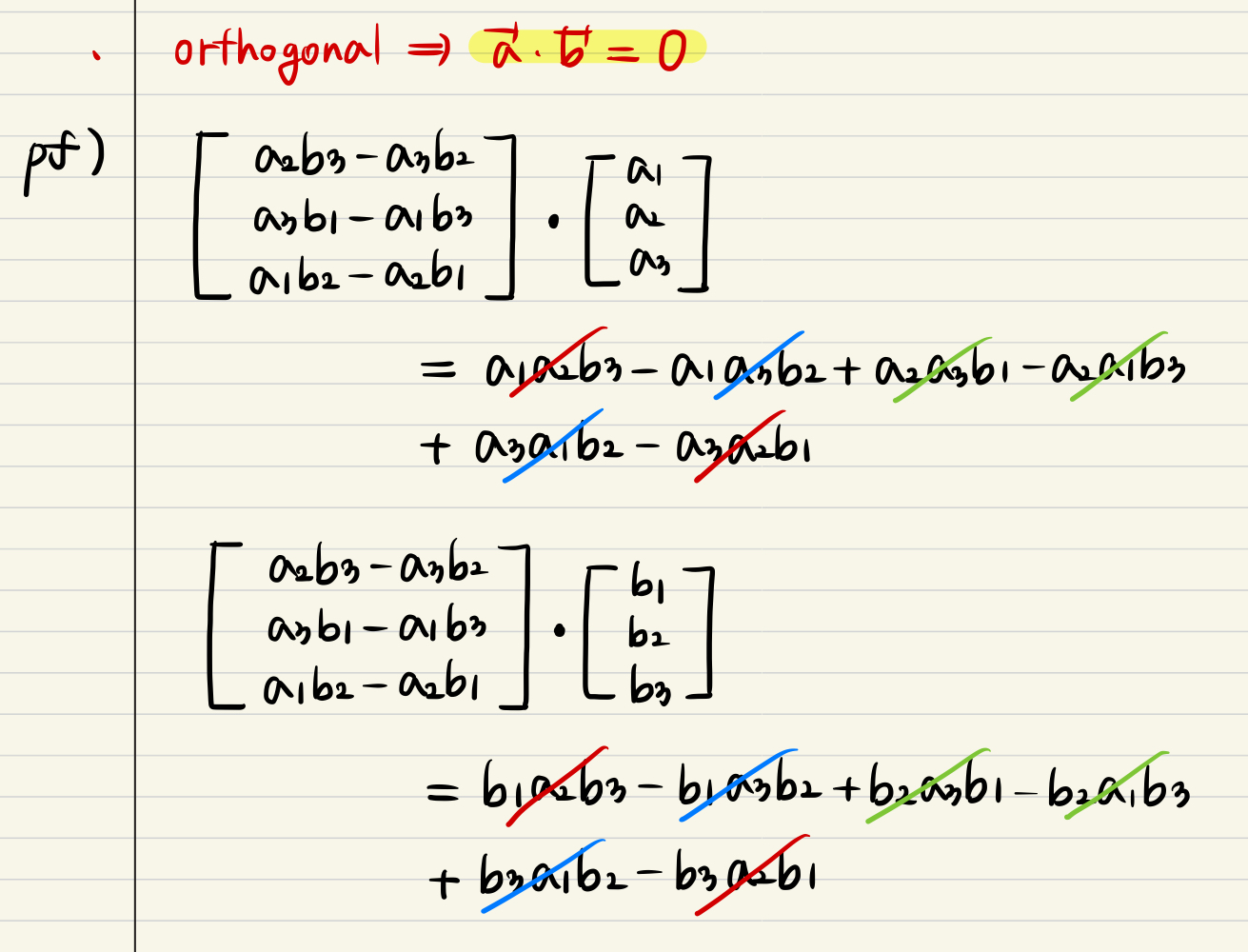
Proof: Relationship between cross product and sin of angle

• There are definitions of relationship between dot product & cross product

Dot & Cross product comparison / intuition

• Dot is the product of "lengths" of vectors which has same direction!
  cf. 'soh cah toa' means the american's expression of sin, cos, tan

• Cross is the product of how much "perpendicular" part each vectors have.
• The magnitude of cross product is a parallelogram area of both vectors!

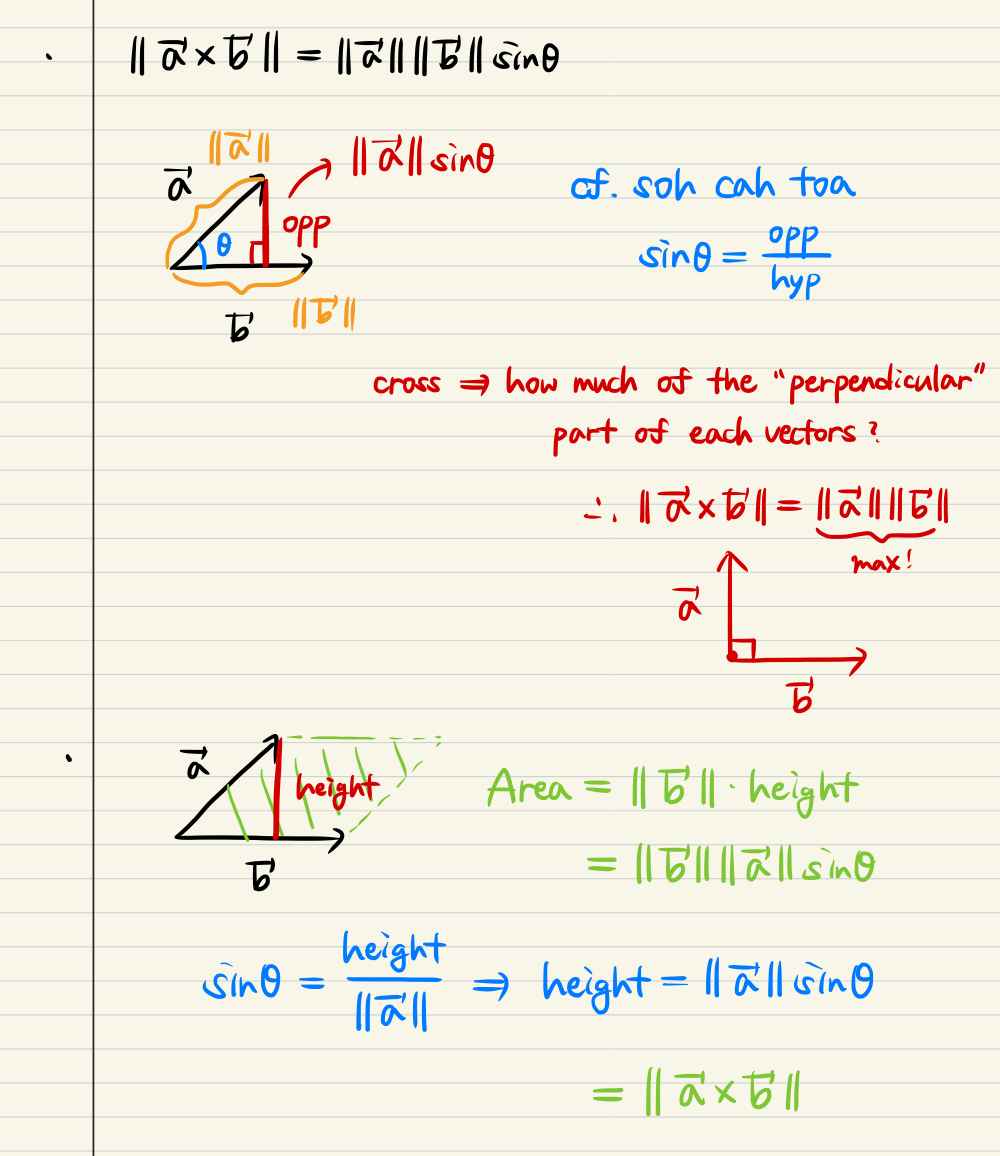
Vector triple product expansion

• This can be a bac-cap fomula : a × (b × c) = vec b (a • c) - vec c (a • b)
  

Normal vector from plane equation

• When we know one point in the plane and normal vector, we can assume plane equation by picking an arbitrary point like (x, y, z)
• It means that the subtraction of two points(p-p') is on the plane and can be orthogonal to normal vector!
• We used to prove it the dot product

Point distance to plane

• When we know one point in the plane and normal vector, and also you get the point which is out of the plane, we can calculate distance from point to the plane!
• We can prove it by using dot product vec f & normal vec, and angular of cosine!
  • f is the subtraction vector from plane to out-of-point

Distance between planes

• We'll use one point of the plane(vec a) and another(vec b) which is in the same plane
• Then calculate the normal vector from both of them
  • A is -1!
• We can get the distance from one plane to the point, which is in another plane, using for the formula right before!