벡터와 공간 | 연립방정식을 풀기 위한 행렬

Matrices : reduced row echelon form

Part 1

• What is it? And Why we should do this?

  • The form is like an augemented matrix and contains eliminated rows.
  • We can find out the pivot valriables and free variables.

• It might be has two rules.

  1. The pivot entry, leading 1 in each row, should be sorted by the previer component of x, like x1 ... xn.
  2. The zeroed out row must be set the last one of the rows.

• Reduced Row Echelon Form A matrix is called rref(A).

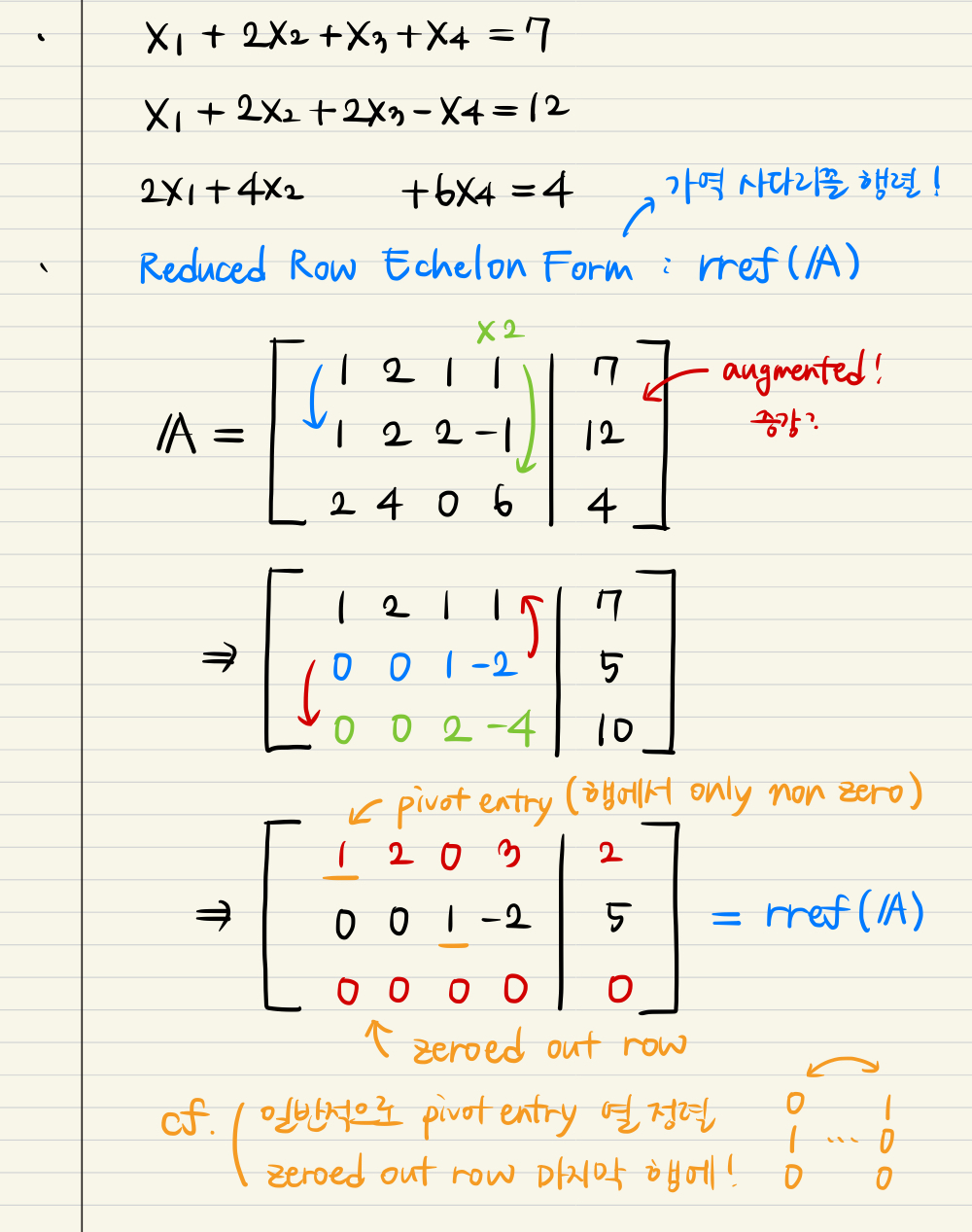
• Example
  • When we completed rref, x1 and x3 can be expressed by combination of x2 or x4.
    • In this example,
      pivot(basic) variables : x1 and x3 / free variables : x2 and x4.
  • Which means we could span the space, using the linear combination of constant, and x2 & x4 vectors.
  • It seems like a plane in the 4 dimension of real space.

Part 2

• Another example
  • After defined rref, we can put it in the (x, y, z) or (x1, x2, x3) solution easily.

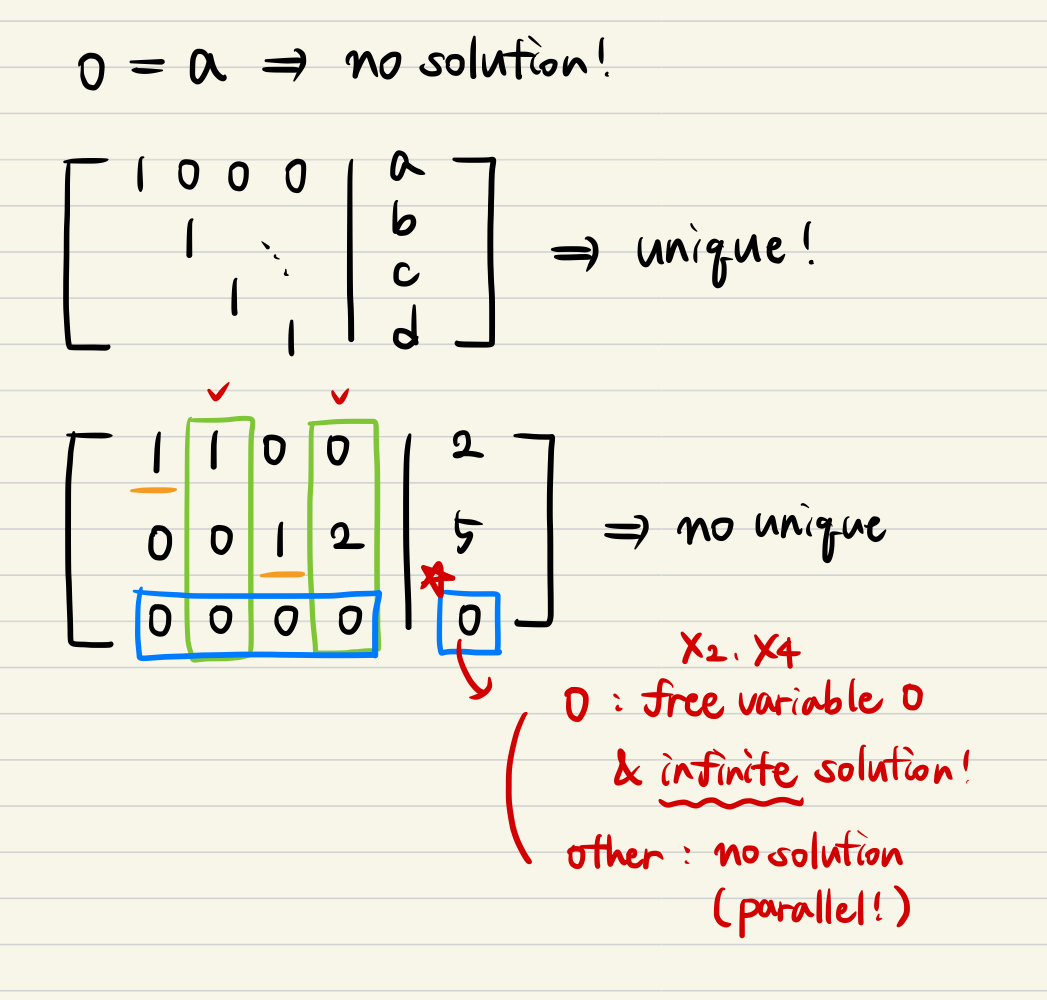
• But if we got the last row represented impossible like 0 = C, it means the spans of vectors are parellel, in other words it has no solution!

Part 3

• Two more thing we should keep in mind this.
  • If we find out the each component of x vecter is a pivot entry, the solution is unique.
  • And If we get the zeroed out row represented like 0 = 0, it means not we have no solution, but infinite solution!