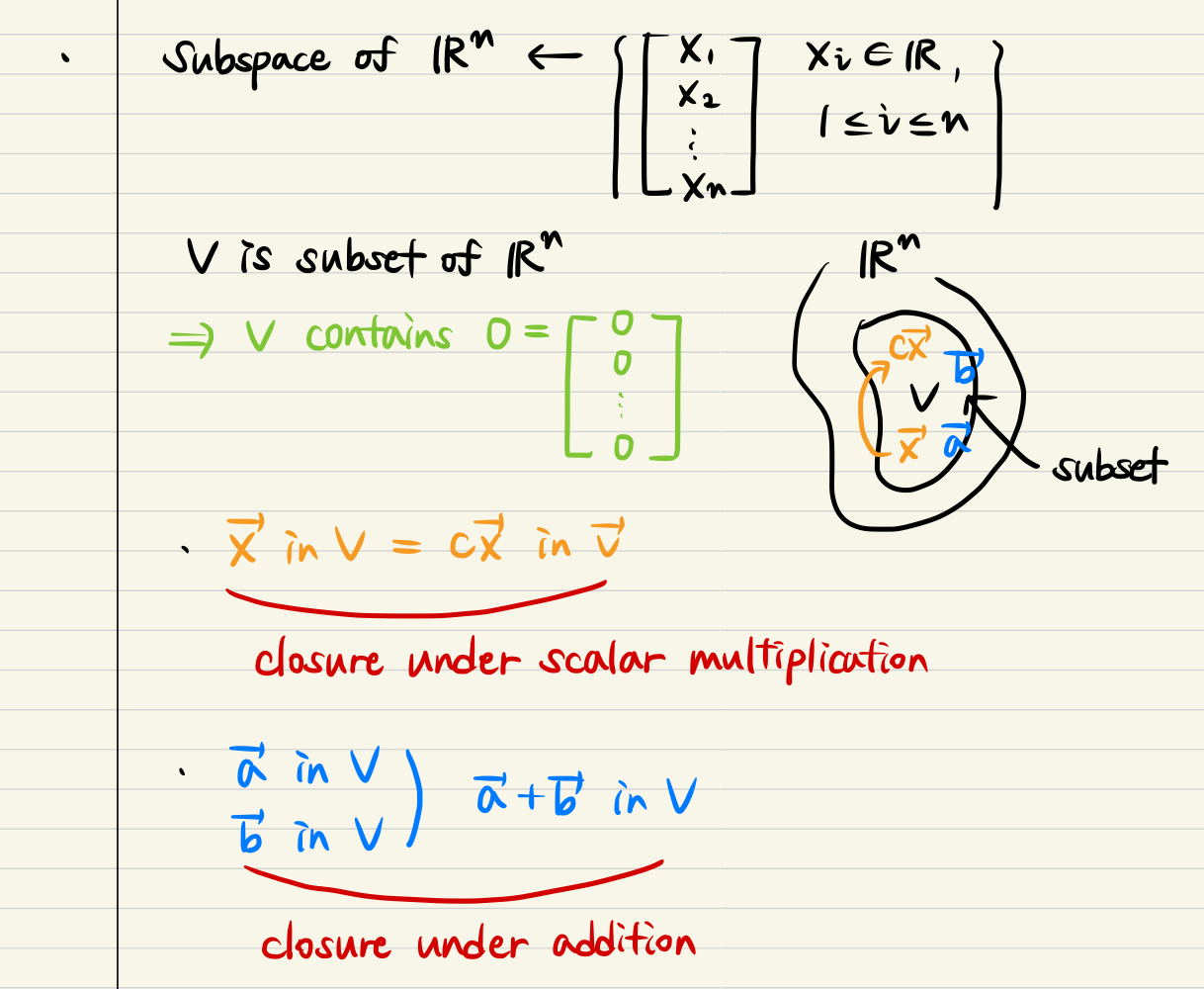
Linear Subspace
- V is a subset of real space
- If x vector is in V, cx vec is also in there
- closure under scalar multiplication
- Else if a vec and b vec are in V, a+b vec is also !
- closure under addition
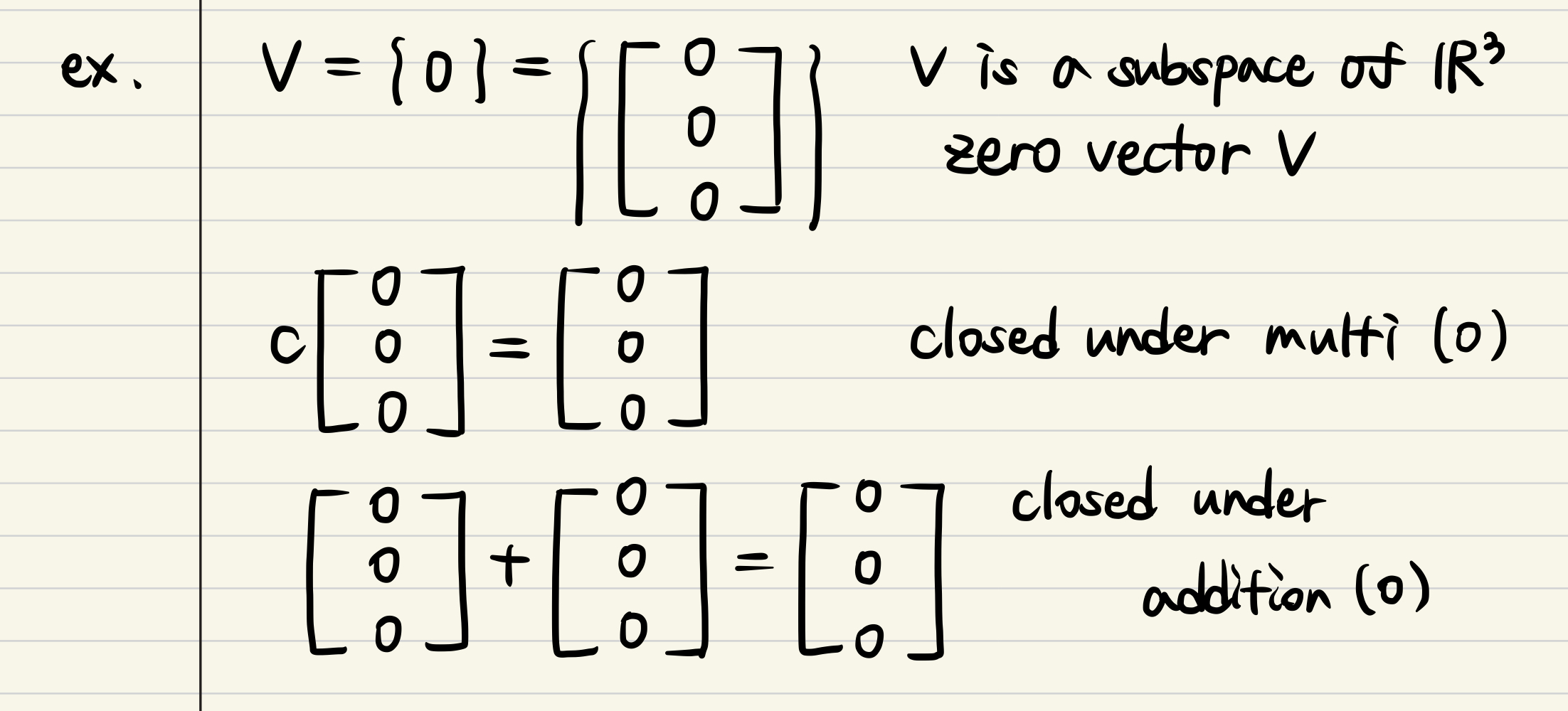
- For example, V is a subspace of R^3 included zero vec
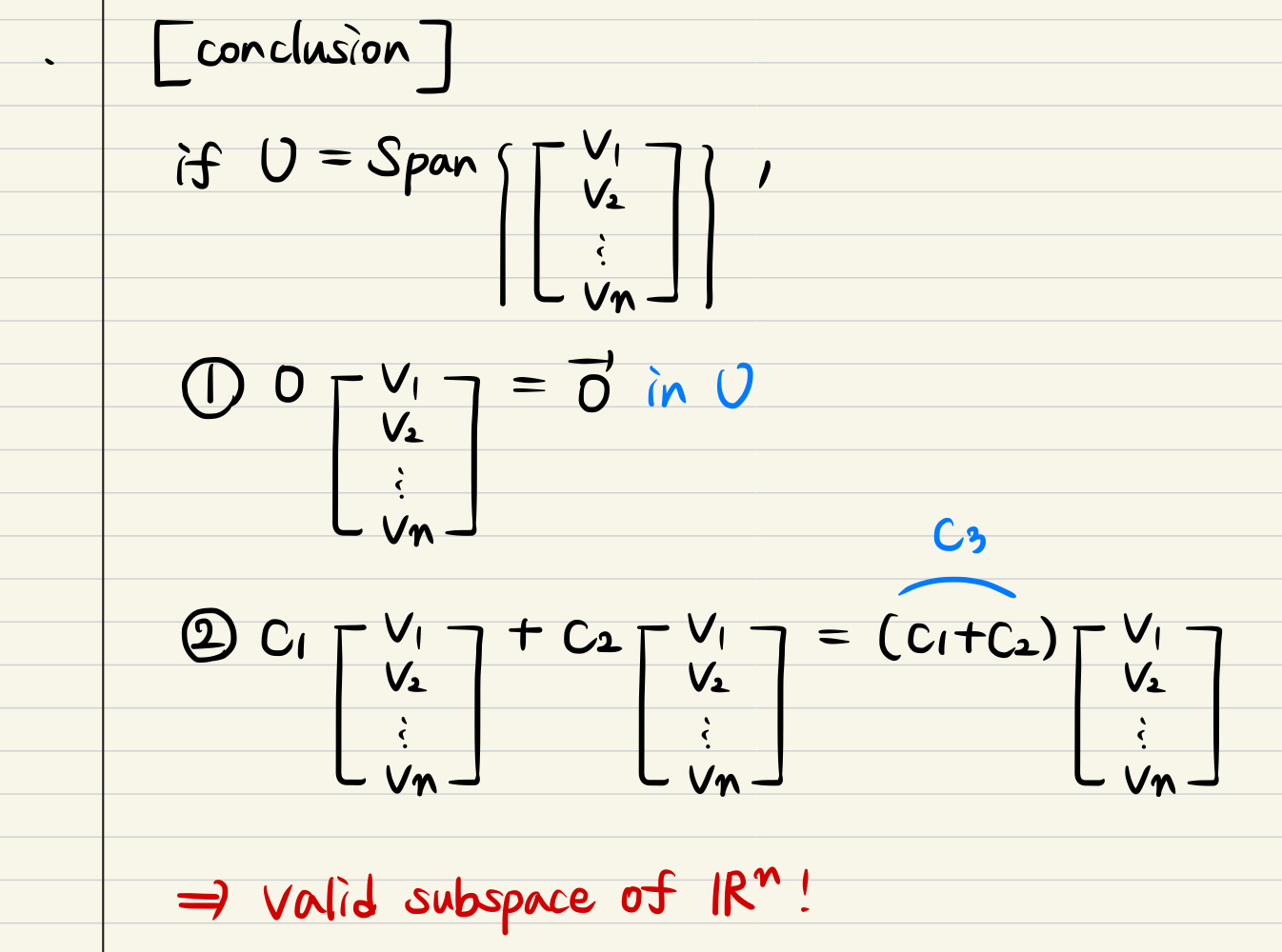
- What if Span of vector? Is it valid for subspace of R?
- Conclusionally, Span of vector like U closed under multiplication, even zero constant, and be represented by linear combination of vectors in that space is valid for subspace of R !
Basis of a subspace
- When V is a subspace of R and S is a span of V,
if it can be linearly independent all of them, S is a basis for V! - But if it had redundence, this is not a basis for V
- Basis means "minimum" set of vectors that spans the subspace!
- For example,
- It needs unique constant to be represented by linear combination
물리학 전공자의 프로그래밍 도전기