벡터와 공간 | 선형종속과 독립

Linearly dependent and Linearly independent

• When the spanning (vec v1, vec v2) is colinear : linear dependent
• It can not represent the other dimensions by using linear combination
• Not only spanning (vec v1, vec v2), but also spanning (v1, v2, v3 combination of v1 & v2) represented in 2 dimensional real space <not in 3D>

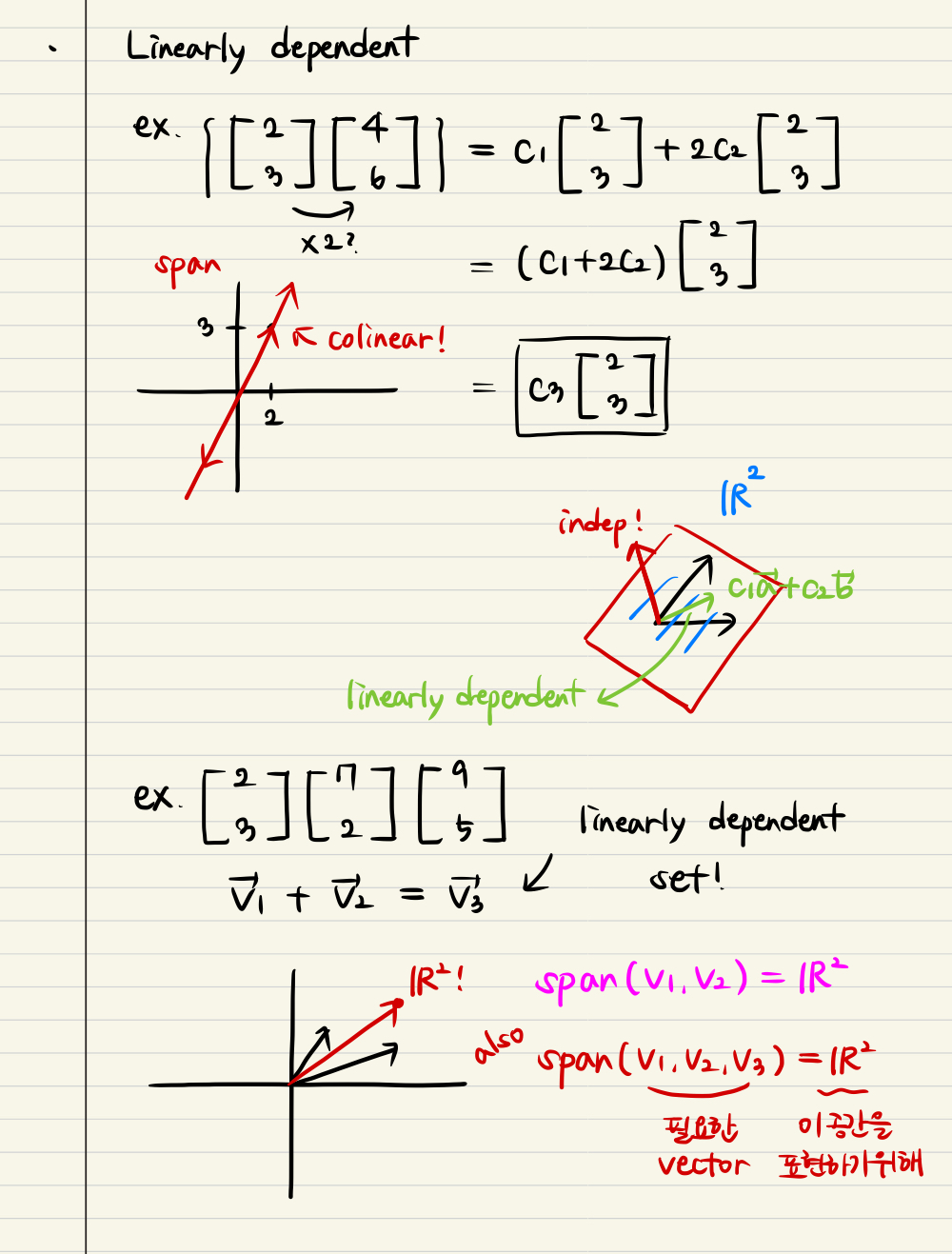
• If vectors are basis, these are linearly independent
• We can span the space more efficient, using the minimum sets of vectors

Definition of Linear Dependence

• If and only if,
  S = {v1, v2, ... vn | linearly dependent} ↔ c1v1 + c2v2 + ... cnvn = 0
  • for some ci's not all are zero, at least 1 is non-zero

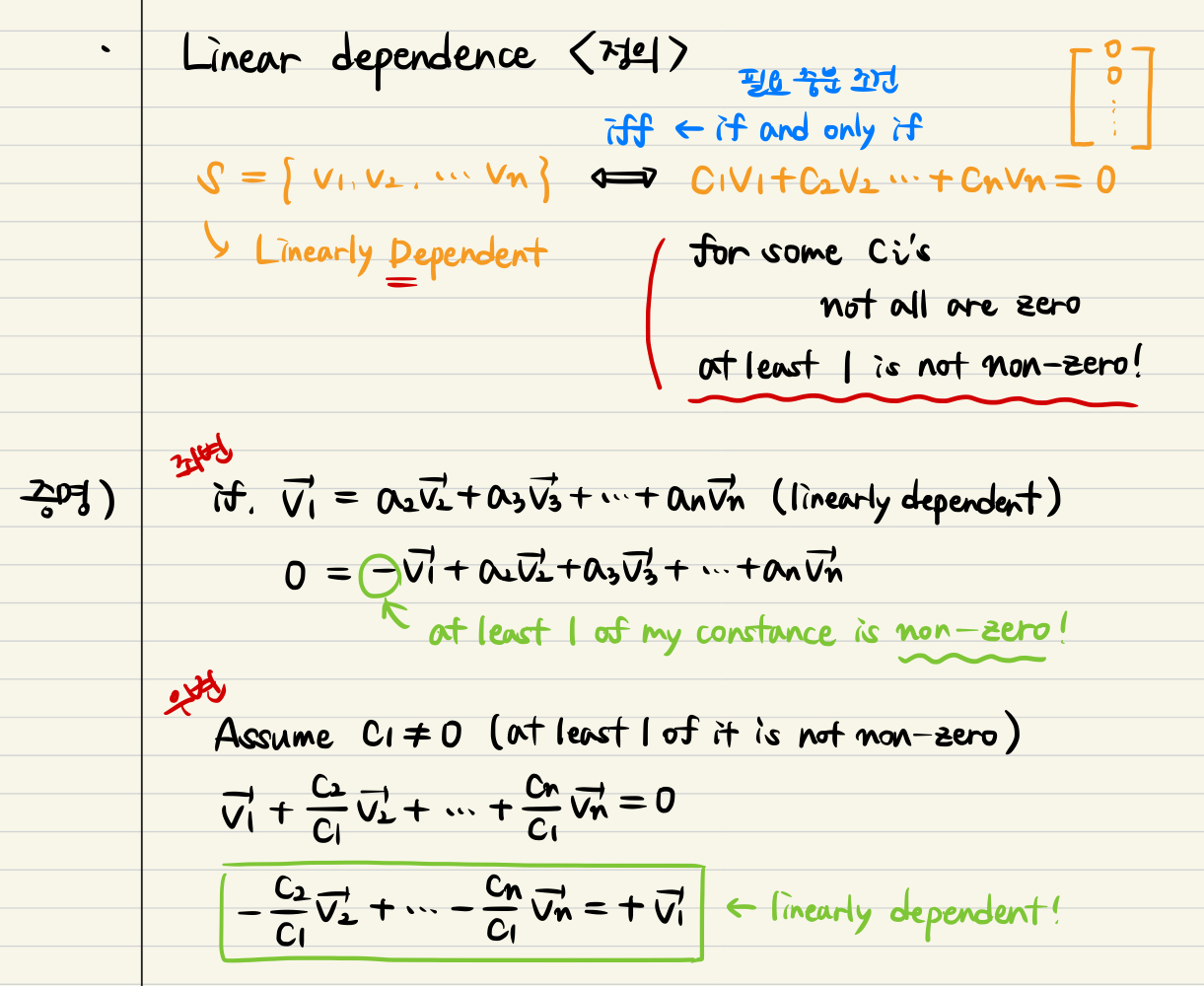
• When we get the vec v1 and vec v2, linear combination of them is 0
  • Case 1 : the const c1 or c2 is non zero → dependent
  • Case 2 : the const c1 and c2 both of'em are zero → independent

• Examples

• Final example of 3 dimension