참고 자료: https://bskyvision.com/entry/%EC%84%A0%ED%98%95%EB%8C%80%EC%88%98%ED%95%99-%EB%86%88norm%EC%9D%B4%EB%9E%80-%EB%AC%B4%EC%97%87%EC%9D%B8%EA%B0%80
https://seongyun-dev.tistory.com/52

p-norm

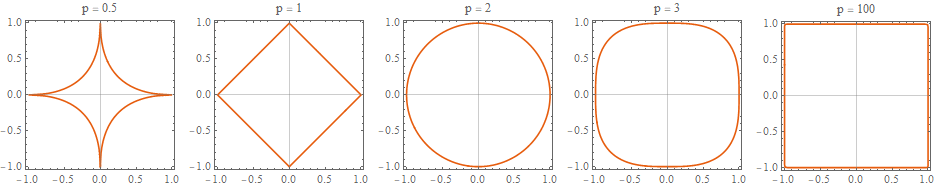
2차원 벡터 공간에서 p값 변화에 따른 p-norm의 분포 형태 (출처 : https://ekamperi.github.io/machine%20learning/2019/10/19/norms-in-machine-learning.html)

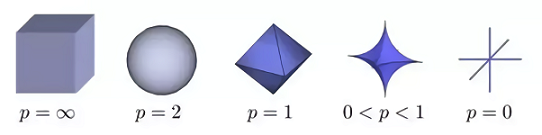
3차원 벡터 공간에서 p값 변화에 따른 p-norm의 분포 형태 (출처 : https://wikidocs.net/21467)

p값이 0일 경우, 특성을 온전히 반영하는 데에 불과하고
p값이 커질 수록 특성을 반영하는 범위를 차례차례 넓혀갈 수 있다. 실제 Global Optimum을 학습할 때, 범위 중 최소 거리에 해당하는 곳을 최적값으로 가정하고 학습할 수 있다.

L1-norm(Lasso)

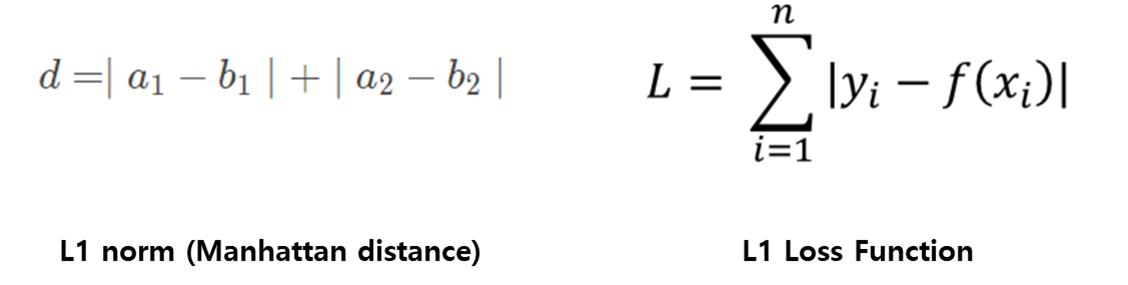
일반적으로 맨하탄 거리로 통하는 L1-norm은 실제 값과 예측 값 사이의 오차에 절댓값을 모두 합한 값이다.

L2-norm(Ridge)

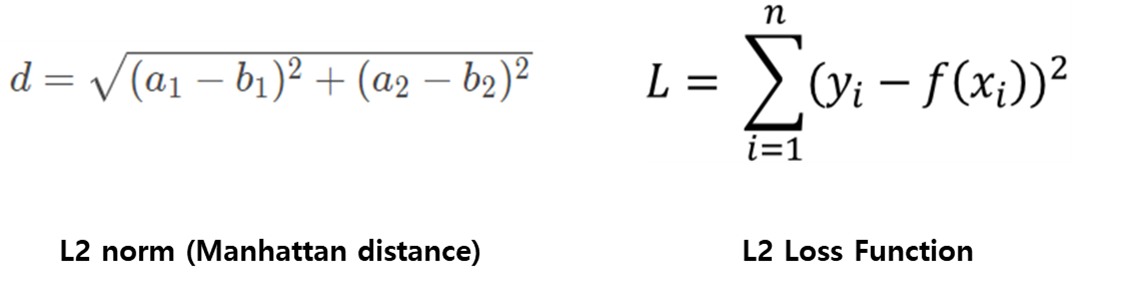
L2-norm은 유클리드 거리로 실제 값과 예측 값 사이의 오차에 대한 제곱 합이다.

Lasso & Ridge 비교

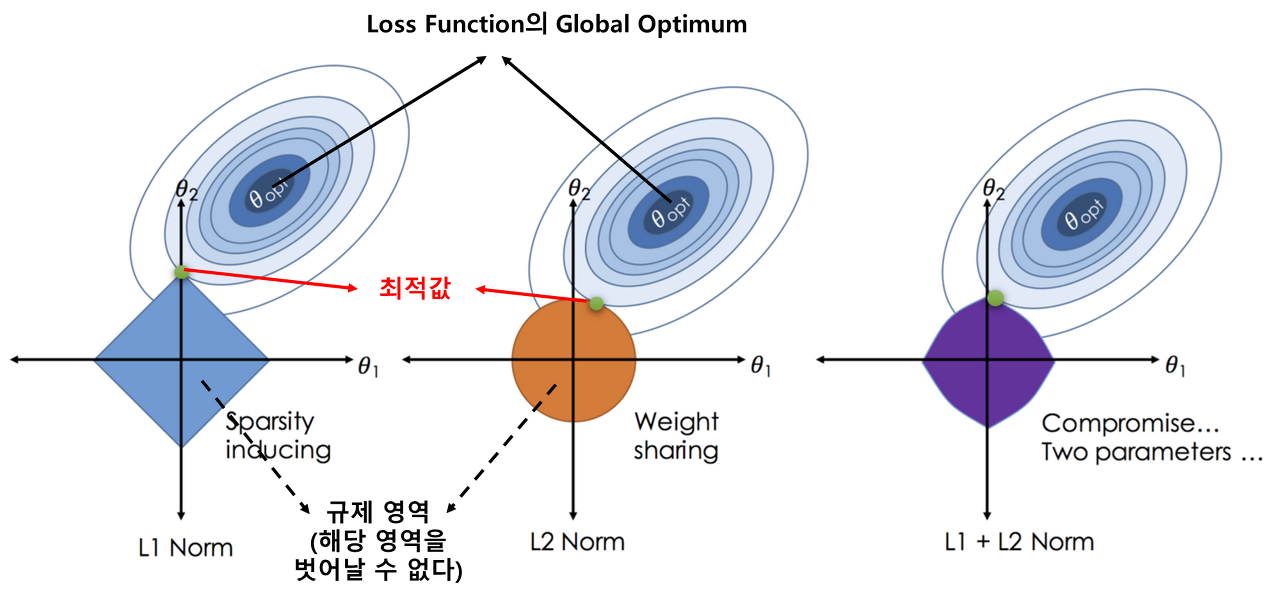
L1, L2 Regularization과 Loss Function 관계 (출처 : https://medium.datadriveninvestor.com/the-art-of-regularization-caca8de7614e)

위 사진이 설명하는 내용을 한눈에 알아보기 어려울 수 있다.
좌표 공간 = feature space, θ1과 θ2는 각각의 feature에 대한 계수를 도메인으로 가지는 변수로 생각하면 간단하게 이해할 수 있을 것이다. L1 Norm의 예시를 보면 θ1의 값이 0일때 최적의 값을 가지는 것을 확인할 수 있다. 이때 θ1의 값이 0이므로 실제 feature의 계수로 0이 반영되면 해당 feature는 사실 상 최적해(Global Optimum)를 찾는데 전혀 기여하지 못한다는 사실을 도출할 수 있다. 따라서 자연스럽게 feature selection의 기능도 수행하게 된다. 또한 예시에서는 설명의 편의를 위해 feature가 2개인 경우를 상정하고 만들어져 있지만 실제로는 수십개의 차원으로 이루어진 feature space에 L1 Norm이 수행된다면 훨씬 많은 feature에 대해 selection이 가능할 수 있다.

하지만 L2 Norm의 경우에는 실질적으로(유클리드 공간에서) 최적해(Global Optimum)에 가장 가까운 feature 계수를 찾는데 더 도움이 된다. 실제로 별로 도움이 되지 못하는 feature를 완전히 제거하지는 못하지만 학습 결과가 더 잘나오는 데에는 기여할 수 있다. 예시를 볼 때에는 별로 와닿지 못할 수 있지만 최적해(Global Optimum)이 θ1또는 θ2축에 치우쳐 있다면 feature를 온전히 반영하지 않는 편이 낫다고 생각하게 될 것이다.

정리하자면 L1 Norm은 특정 feature를 완전히 제거할 수 있어 휴리스틱 측면에서는 이점으로 다가올 수 있지만 언더피팅의 위험이 존재하고 L2 Norm은 모든 feature를 반영하기 때문에 학습 정확도 측면에서는 좋은 성능을 보여줄 수 있지만 학습 데이터에서만 유의미하게 나타나는 feature 관계를 학습하는 오버피팅의 위험이 존재한다.