[백준 2253] 점프 (Python)

백준 2253 - 점프

코드

BFS를 이용한 풀이

import sys
from collections import deque

N, M = map(int, sys.stdin.readline().split())
check = [[] for _ in range(N + 1)]
small_rock = set()
for _ in range(M):
    small = int(sys.stdin.readline())
    small_rock.add(small)

def solution(N, check, small_rock):
    queue = deque([(1, 0, 0)])
    while queue:
        location, jump, n = queue.popleft()
        for x in [jump + 1, jump, jump - 1]:
            if x > 0:
                next_location = location + x
                if next_location == N:
                    return n + 1
                if next_location < N and next_location not in small_rock and x not in check[next_location]:
                    check[next_location].append(x)
                    queue.append((next_location, x, n + 1))
    return -1 

print(solution(N, check, small_rock))

DP를 이용한 풀이

import sys
N, M = map(int, sys.stdin.readline().split())
dp = [[float('inf')] * (int((2 * N)** 0.5) + 2) for _ in range(N + 1)] 
dp[1][0] = 0

stone_set = set()
for _ in range(M):
    stone_set.add(int(sys.stdin.readline()))
for i in range(2, N + 1):
    if i in stone_set:
        continue
    for j in range(1, int((2 * i) ** 0.5) + 1):
        dp[i][j] = min(dp[i - j][j - 1], dp[i - j][j], dp[i - j][j + 1]) + 1

if min(dp[N]) == float('inf'):
    print(-1)
else:
    print(min(dp[N]))

문제를 보고 어떻게 DP로 풀어야할 지 감이 안잡혀서 BFS로 먼저 풀고 DP는 다른 풀이들을 보고 공부하며 코드를 작성해보았다.

풀이

1. BFS를 이용한 풀이

이 문제에서 BFS를 이용하려면 이미 방문했던 돌이어도 그때와 다른 속도라면 재방문이 가능하다는 점을 고려해야한다.

아래의 그림은 도착점이 8이고 3, 6에는 방문이 불가능한 예제이다.

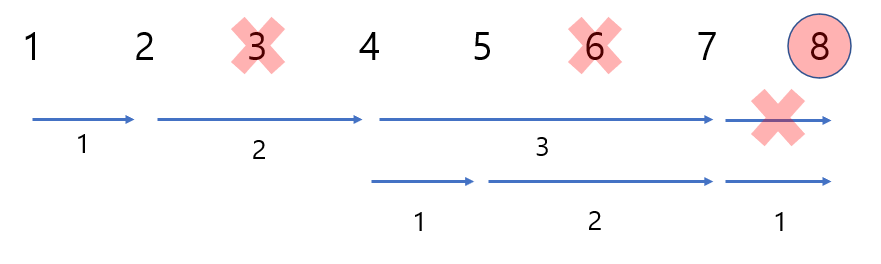
BFS를 진행했을때 4에서 속도가 3인 상태로 7에 처음으로 도착할 것이다. 이 때 다음으로 점프가 가능한 속도는 2, 3, 4, 이므로 8에는 도달할 수 없다.
이때 7에 방문체크를 해 재방문이 불가능하게 한다면 8은 도달할 수 없는 점이 된다.
하지만 3과 다른 속도일 때는 방문을 허용한다면 5에서 속도가 2인 상태로 7에 방문하게 되고 8은 도달할 수 있는 점이 된다.
따라서 BFS를 구현하되 각 돌의 방문을 체크하는 리스트에 돌에 방문했을 때의 속도를 담아 동일한 속도면 방문할 수 없고 다른 속도라면 방문할 수 있도록 한다면 문제를 해결할 수 있다.

2. DP를 이용한 풀이

이때 int((2 * N) ** 0.5) + 1는 1부터 속도가 끊임없이 1씩 증가하며 점프할 때 N에 도달했을 때의 속도의 근사값이다.
즉 첫째항이 1이고 공차가 1인 등차수열에서 수열의 합이 N이 될 때 마지막 항의 값의 근사값이고 아래와 같은 과정을 거쳐 이 값을 얻을 수 있다.

K * (K + 1) / 2 = N
K ** 2 + K = 2N 
K = (2N - K) ** 0.5 < 2N ** 0.5

그리고 i를 현재 위치, j를 현재 속도라고 했을 때
dp[i][j] = min(dp[i - j][j - 1], dp[i - j][j], dp[i - j][j + 1]) + 1
이라는 점화식을 얻을 수 있다.
이 점화식은 i라는 점에 j의 속도로 도달했을 때의 최소 점프횟수는 i - j의 위치에 각각 j - 1, j, j + 1의 속도로 도달했을 떄의 최소 점프횟수 + 1이라는 뜻이다.
j - 1, j, j + 1의 속도에서 각각 +1, +0, -1을 했을 때 j만큼 점프할 수 있기 때문에 i - j에서 i로 갈 수 있기 때문이다.
그리고 이 때 j의 최대값은 int((2 * i) ** 0.5) + 1이다. 이는 앞에서 설명했듯이 1에서부터 속도가 끊임없이 증가하며 점프할 때 i에 도달했을 때의 속도의 근사값이다.
위 내용을 이해했다면 어려움 없이 문제를 해결할 수 있을 것이다.

dp는 어렵다.

피드백 환영합니다.
-끝-