[백준 9251] LCS (파이썬)

백준 9251 - LCS

import sys

string_a = ' ' + sys.stdin.readline().rstrip()
string_b = ' ' + sys.stdin.readline().rstrip()
dp = [[0] * len(string_b) for _ in range(len(string_a))]

for i in range(1, len(string_a)):
    for j in range(1, len(string_b)):
        if string_a[i] == string_b[j]:
            dp[i][j] = dp[i - 1][j - 1] + 1
        else:
            dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
            
print(dp[-1][-1])

풀이를 찾아봐도 쉽게 이해되지 않아 직접 정리하며 이해하기 위해 포스팅을 하게 되었다.
DP 문제는 내가 똑똑하지 않다는 것을 너무 적나라하게 보여주지만 풀었을 때의 쾌감도 다른 문제보다 큰 것 같다.

풀이

먼저 이번 문제의 점화식은 아래와 같다.

LCS(Xi, Yj)를 문자열 X, Y 각각의 i, j번째 글자까지의 최장 공통 부분 문자열의 길이라고 했을 때

X[i] == Y[j]일 때
LCS(Xi, Yj) = LCS(Xi - 1, Yj - 1) + 1

X[i] != Y[j]일 때
LCS(Xi, Yj) = LCS(Xi - 1, Yj - 1)
LCS(Xi, Yj) = max(LCS(Xi - 1, Yj), LCS(Xi, Yj - 1))

이제 점화식을 하나씩 뜯어서 살펴보자.

1. X[i] == Y[j]

먼저 X[i] == Y[j]일 때는 각 문자열에 X[i], Y[j]가 추가되기
이전의 LCS의 길이(= LCS(Xi - 1, Yj - 1))에 1만큼 더해주면 된다.
이는 직관적으로 이해할 수 있다.

2. X[i] != Y[j]

다음으로 X[i] != Y[j]일 때 마지막 글자가 다르다고 각 문자열에 X[i], Y[j]가 추가되기 이전의 LCS의 길이(= LCS(Xi - 1, Yj - 1))를 그대로 가져오면 LCS의 길이를 손해볼 수 있다.
문자열 ACB와 ABA를 예로 들어보자. 문자열 ACB와 ABA의 LCS는 AB이다. 하지만 마지막 글자인 B와 A가 다르다고 LCS(X3 - 1, Y3 - 1)를 그대로 가져오면 LCS는 A가 되어 버리는 것이다.
그래서 우리는 마지막 글자가 다를 때에는 각 문자열의 마지막 글자들이 따로 한 글자씩 추가 되었을 때의
LCS (= LCS(Xi - 1, Yj), LCS(Xi, Yj - 1) ) 중 큰값을 가져와야 한다.

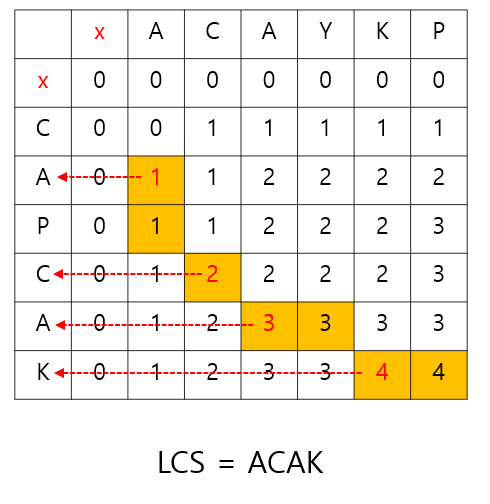
문제의 예시인 ACAYKP와 CAPCAK의 LCS를 구하는 과정을 표로 나타내면 아래와 같다.

똑똑한 사람이 되자.

피드백 환영합니다.
-끝-